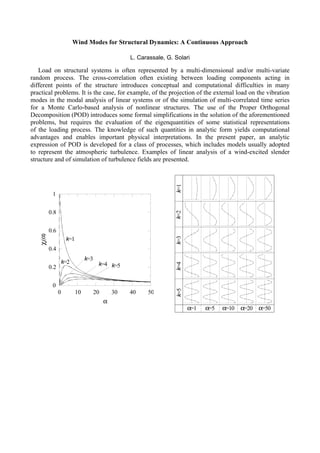
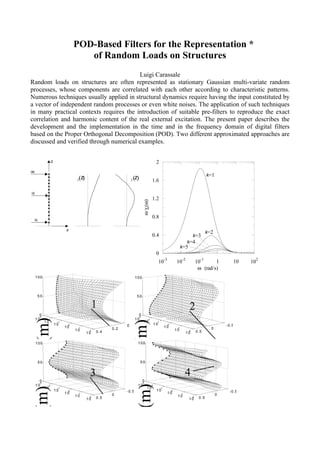
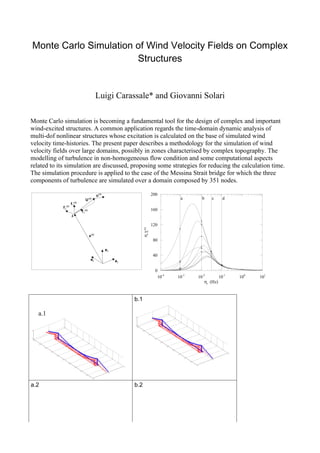
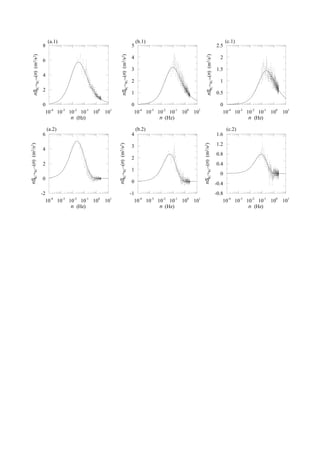
The document discusses the double modal transformation technique for analyzing the dynamic response of linear structures subjected to stochastic loading. It proposes a method called double modal transformation that simultaneously transforms the equations of motion and the loading process. This allows the structural response to be obtained through a double series expansion where structural and loading modal contributions are superimposed. The effectiveness of this technique is illustrated through two classic wind engineering problems: alongwind response and vortex-induced crosswind response of slender structures.