1. The document provides examples and concepts related to limits, including definitions, evaluating limits of various functions as the variable approaches a number, and evaluating one-sided and two-sided limits. 2. Worked examples evaluate limits of rational functions, radical functions, and trigonometric functions as the variable approaches numbers or infinity. 3. Key concepts such as left-hand and right-hand limits, and limits at infinity, are demonstrated through multiple examples.

1. CHAPTER 1 Limits
x3 – 4 x 2 + x + 6
1.1 Concepts Review 9. lim
x → –1 x +1
1. L; c ( x + 1)( x 2 – 5 x + 6)
= lim
x → –1 x +1
2. 6
= lim ( x 2 – 5 x + 6)
x → –1
3. L; right
= (–1) – 5(–1) + 6
2
4. lim f ( x) = M = 12
x →c
x 4 + 2 x3 – x 2
10. lim
Problem Set 1.1 x →0 x2
= lim( x 2 + 2 x –1) = –1
1. lim( x – 5) = –2 x →0
x →3
2. lim (1 – 2t ) = 3 x2 – t 2 ( x + t )( x – t )
t → –1
11. lim = lim
x→–t x + t x→ – t x+t
= lim ( x – t )
3. lim ( x 2 + 2 x − 1) = (−2) 2 + 2(−2) − 1 = −1 x→ –t
x →−2 = –t – t = –2t
4. lim ( x 2 + 2t − 1) = (−2) 2 + 2t − 1 = 3 + 2t x2 – 9
x →−2 12. lim
x →3 x – 3
(
5. lim t 2 − 1 =
t →−1
) ( ( −1) − 1) = 0
2
= lim
x →3
( x – 3)( x + 3)
x–3
= lim( x + 3)
(
6. lim t 2 − x 2 =
t →−1
) ( ( −1) 2
)
− x2 = 1 − x2 x →3
=3+3=6
x2 – 4 ( x – 2)( x + 2) (t + 4)(t − 2) 4
7. lim = lim 13. lim
x→2 x – 2 x→2 x–2 t →2 (3t − 6) 2
= lim( x + 2)
x→2 (t − 2) 2 t + 4
= lim
=2+2=4 t →2 9(t − 2) 2
t 2 + 4t – 21 t+4
8. lim = lim
t →2 9
t → –7 t+7
(t + 7)(t – 3) 2+4 6
= lim = =
t → –7 t+7 9 9
= lim (t – 3)
t → –7
(t − 7)3
= –7 – 3 = –10 14. lim
t →7+ t −7
(t − 7) t − 7
= lim
t →7 + t −7
= lim t −7
t →7+
= 7−7 = 0
Instructor’s Resource Manual Section 1.1 63
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

2. x 4 –18 x 2 + 81 ( x 2 – 9) 2 1 − cos t
15. lim = lim lim =0
x →3 2 x →3 2 t →0 2t
( x – 3) ( x – 3)
( x – 3) 2 ( x + 3) 2 ( x − sin x ) 2 / x 2
= lim 2
= lim( x + 3)2 = (3 + 3) 2 21. x
x →3 ( x – 3) x →3
1. 0.0251314
= 36
0.1 2.775 × 10−6
(3u + 4)(2u – 2)3 8(3u + 4)(u –1)3 0.01 2.77775 × 10−10
16. lim = lim
u →1 (u –1) 2 u →1 (u –1) 2 0.001 2.77778 × 10−14
= lim 8(3u + 4)(u – 1) = 8[3(1) + 4](1 – 1) = 0
u →1 –1. 0.0251314
–0.1 2.775 × 10−6
(2 + h) 2 − 4 4 + 4h + h 2 − 4
17. lim = lim –0.01 2.77775 × 10−10
h→0 h h→0 h
h 2 + 4h –0.001 2.77778 × 10−14
= lim = lim(h + 4) = 4
h →0 h h →0 ( x – sin x) 2
lim =0
x →0 x2
( x + h) 2 − x 2 x 2 + 2 xh + h 2 − x 2
18. lim = lim 2 2
h→0 h h →0 h 22. x (1 − cos x ) / x
h 2 + 2 xh 1. 0.211322
= lim = lim(h + 2 x) = 2 x
h →0 h h →0 0.1 0.00249584
0.01 0.0000249996
19. x sin x 0.001 2.5 × 10−7
2x
1. 0.420735
–1. 0.211322
0.1 0.499167
–0.1 0.00249584
0.01 0.499992 –0.01 0.0000249996
0.001 0.49999992 –0.001 2.5 × 10−7
(1 – cos x) 2
–1. 0.420735 lim =0
x →0 x2
–0.1 0.499167
2
23. t (t − 1) /(sin(t − 1))
–0.01 0.499992
–0.001 0.49999992 2. 3.56519
1.1 2.1035
sin x
lim = 0.5 1.01
x →0 2 x 2.01003
1.001 2.001
1− cos t
20. t 2t
1. 0.229849 0 1.1884
0.1 0.0249792 0.9 1.90317
0.01 0.00249998 0.99 1.99003
0.999 1.999
0.001 0.00024999998
t −12
lim =2
–1. –0.229849 t →1 sin(t − 1)
–0.1 –0.0249792
–0.01 –0.00249998
–0.001 –0.00024999998
64 Section 1.1 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

3. 27. x ( x − π / 4) 2 /(tan x − 1) 2
x −sin( x − 3) − 3
24. x x −3
1. + π
4
0.0320244
π
4. 0.158529 0.1 + 4 0.201002
π
3.1 0.00166583 0.01 + 4 0.245009
π
3.01 0.0000166666 0.001 + 4 0.2495
3.001 1.66667 × 10−7
−1. + π
4 0.674117
2. 0.158529 −0.1 + π
4 0.300668
2.9 0.00166583 −0.01 + π
4 0.255008
2.99 0.0000166666 −0.001 + π
4 0.2505
2.999 1.66667 × 10−7
lim
(x − ) π 2
4
= 0.25
lim
x – sin( x – 3) – 3
=0 x→ π
4 (tan x − 1)2
x →3 x–3
28. u (2 − 2sin u ) / 3u
25. x (1 + sin( x − 3π / 2)) /( x − π )
1. + π 0.11921
1. + π 0.4597 2
0.1 + π 0.00199339
0.1 + π 0.0500
2
0.01 + π 0.0000210862
0.01 + π
2
0.0050 0.001 + π
2.12072 × 10−7
2
0.001 + π 0.0005
−1. + π
2 0.536908
–1. + π –0.4597 −0.1 + π
2 0.00226446
–0.1 + π –0.0500 −0.01 + π
0.0000213564
2
–0.01 + π –0.0050 −0.001 + π
2.12342 × 10−7
2
–0.001 + π –0.0005 2 − 2sin u
lim =0
1 + sin ( x − 32π ) u→ π 3u
2
lim =0
x →π x−π
29. a. lim f ( x) = 2
x → –3
26. t (1 − cot t ) /(1 / t )
b. f(–3) = 1
1. 0.357907
0.1 –0.896664 c. f(–1) does not exist.
0.01 –0.989967
5
0.001 –0.999 d. lim f ( x) =
x → –1 2
–1. –1.64209 e. f(1) = 2
–0.1 –1.09666 f. lim f(x) does not exist.
x→1
–0.01 –1.00997
–0.001 –1.001 g. lim f ( x) = 2
x →1–
1 – cot t
lim 1
= –1
t →0
t h. lim f ( x) = 1
x →1+
5
i. lim f ( x ) =
+ 2
x →−1
Instructor’s Resource Manual Section 1.1 65
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

4. 30. a. lim f ( x) does not exist. b. lim f ( x) does not exist.
x → –3 x →1
b. f(–3) = 1 c. f(1) = 2
c. f(–1) = 1 d. lim f ( x) = 2
x →1+
d. lim f ( x) = 2
x → –1
34.
e. f(1) = 1
f. lim f ( x) does not exist.
x →1
g. lim f ( x) = 1
x →1–
h. lim f ( x) does not exist.
x →1+
i. lim f ( x ) = 2
x →−1+
a. lim g ( x) = 0
31. a. f(–3) = 2 x →1
b. f(3) is undefined. b. g(1) does not exist.
c. lim f ( x) = 2
x → –3− c. lim g ( x ) = 1
x→2
d. lim f ( x) = 4
x → –3+ d. lim g ( x ) = 1
x → 2+
e. lim f ( x) does not exist.
x → –3
35. f ( x) = x – ⎡[ x ]⎤
⎣ ⎦
f. lim f ( x) does not exist.
x →3+
32. a. lim f ( x) = −2
x → –1−
b. lim f ( x) = −2
x → –1+
c. lim f ( x) = −2
x → –1
d. f (–1) = –2
e. lim f ( x) = 0
x →1 a. f(0) = 0
f. f (1) = 0 b. lim f ( x) does not exist.
x →0
33.
c. lim f ( x ) = 1
x →0 –
1
d. lim f ( x) =
x→ 1 2
2
a. lim f ( x) = 0
x →0
66 Section 1.1 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

5. x 41. lim f ( x) exists for a = –1, 0, 1.
36. f ( x) = x→a
x
42. The changed values will not change lim f ( x) at
x→a
any a. As x approaches a, the limit is still a 2 .
x −1
43. a. lim does not exist.
x →1 x −1
x −1 x −1
lim = −1 and lim =1
x →1 − x −1 +
x →1 x −1
x −1
b. lim = −1
a. f (0) does not exist. x →1 − x −1
b. lim f ( x) does not exist. x2 − x − 1 − 1
x →0 c. lim = −3
x →1− x −1
c. lim f ( x ) = –1
x →0 –
⎡ 1 1 ⎤
d. lim ⎢ − ⎥ does not exist.
− x −1 x −1 ⎥
d. lim f ( x) = 1 x →1 ⎢
⎣ ⎦
x→ 1
2
44. a. lim x− x =0
x2 − 1 x →1+
37. lim does not exist.
x →1 x − 1
1
x2 − 1 x2 − 1 b. lim does not exist.
lim = −2 and lim =2 x →0 + x
x →1− x −1 x →1+ x − 1
1/ x
x+2− 2 c. lim x(−1) =0
38. lim x → 0+
x →0 x
1/ x
( x + 2 − 2)( x + 2 + 2) d. lim x (−1) =0
= lim x →0+
x →0 x( x + 2 + 2)
x+2−2 x 45. a) 1 b) 0
= lim = lim
x →0 x( x + 2 + 2) x →0 x( x + 2 + 2)
c) −1 d) −1
1 1
2 1
= lim = = = 46. a) Does not exist b) 0
x →0 x+2+ 2 0+2 + 2 2 2 4
c) 1 d) 0.556
39. a. lim f ( x) does not exist.
x →1
47. lim x does not exist since x is not defined
x →0
b. lim f ( x) = 0
x →0 for x < 0.
40. 48. lim x x = 1
x → 0+
49. lim x =0
x →0
x
50. lim x = 1
x →0
sin 2 x 1
51. lim =
x →0 4 x 2
Instructor’s Resource Manual Section 1.2 67
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

6. sin 5 x 5 7. If x is within 0.001 of 2, then 2x is within 0.002
52. lim = of 4.
x →0 3x 3
⎛1⎞
53. lim cos ⎜ ⎟ does not exist.
x →0 ⎝ x⎠
⎛1⎞
54. lim x cos ⎜ ⎟ = 0
x →0 ⎝ x⎠
x3 − 1
55. lim =6
x →1 2x + 2 − 2 8. If x is within 0.0005 of 2, then x2 is within 0.002
of 4.
x sin 2 x
56. lim =2
x →0 sin( x 2 )
x2 – x – 2
57. lim = –3
x →2– x–2
2
58. lim 1/( x −1)
=0
x →1 +
1+ 2
9. If x is within 0.0019 of 2, then 8 x is within
59. lim x ; The computer gives a value of 0, but 0.002 of 4.
x →0
lim x does not exist.
x →0−
1.2 Concepts Review
1. L – ε ; L + ε
2. 0 < x – a < δ ; f ( x) – L < ε 8
10. If x is within 0.001 of 2, then is within 0.002
ε x
3. of 4.
3
4. ma + b
Problem Set 1.2
1. 0 < t – a < δ ⇒ f (t ) – M < ε
2. 0 < u – b < δ ⇒ g (u ) – L < ε 11. 0 < x – 0 < δ ⇒ (2 x – 1) – (–1) < ε
2x – 1+ 1 < ε ⇔ 2x < ε
3. 0 < z – d < δ ⇒ h( z ) – P < ε ⇔ 2 x <ε
ε
4. 0 < y – e < δ ⇒ φ ( y ) – B < ε ⇔ x <
2
5. 0 < c – x < δ ⇒ f ( x) – L < ε
ε
δ = ;0 < x –0 <δ
2
6. 0 < t – a < δ ⇒ g (t ) – D < ε
(2 x – 1) – (–1) = 2 x = 2 x < 2δ = ε
68 Section 1.2 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

7. 12. 0 < x + 21 < δ ⇒ (3x – 1) – (–64) < ε 2 x 2 – 11x + 5
15. 0 < x – 5 < δ ⇒ –9 <ε
3 x – 1 + 64 < ε ⇔ 3 x + 63 < ε x–5
⇔ 3( x + 21) < ε 2 x 2 – 11x + 5 (2 x – 1)( x – 5)
–9 <ε ⇔ –9 <ε
⇔ 3 x + 21 < ε x–5 x–5
ε ⇔ 2x – 1 – 9 < ε
⇔ x + 21 <
3
⇔ 2( x – 5) < ε
ε ε
δ = ; 0 < x + 21 < δ ⇔ x–5 <
3 2
(3 x – 1) – (–64) = 3 x + 63 = 3 x + 21 < 3δ = ε
ε
δ = ;0 < x –5 <δ
2
x 2 – 25
13. 0 < x – 5 < δ ⇒ – 10 < ε 2 x – 11x + 5
2
(2 x – 1)( x – 5)
x–5 –9 = –9
x–5 x–5
x 2 – 25 ( x – 5)( x + 5) = 2 x – 1 – 9 = 2( x – 5) = 2 x – 5 < 2δ = ε
– 10 < ε ⇔ – 10 < ε
x–5 x–5
⇔ x + 5 – 10 < ε 16. 0 < x – 1 < δ ⇒ 2x – 2 < ε
⇔ x–5 <ε
2x – 2 < ε
δ = ε; 0 < x – 5 < δ ( 2 x – 2 )( 2 x + 2 )
⇔ <ε
2x + 2
2
x – 25 ( x – 5)( x + 5)
– 10 = – 10 = x + 5 – 10
x–5 x–5 2x – 2
⇔ <ε
= x–5 <δ =ε 2x + 2
x –1
⇔2 <ε
2x – x 2 2x + 2
14. 0 < x – 0 < δ ⇒ − (−1) < ε
x
2ε
2 x2 – x x(2 x – 1) δ= ; 0 < x –1 < δ
+1 < ε ⇔ +1 < ε 2
x x ( 2 x – 2)( 2 x + 2)
2x − 2 =
⇔ 2x – 1 +1 < ε 2x + 2
⇔ 2x < ε 2x – 2
=
⇔ 2 x <ε 2x + 2
ε 2 x –1 2 x – 1 2δ
⇔ x < ≤ < =ε
2 2x + 2 2 2
ε 2x – 1
δ = ;0 < x –0 <δ 17. 0 < x – 4 < δ ⇒ – 7 <ε
2 x–3
2 x2 – x x(2 x – 1)
− (−1) = + 1 = 2x – 1+ 1 2x – 1 2 x – 1 – 7( x – 3)
x x – 7 <ε ⇔ <ε
x–3 x–3
= 2 x = 2 x < 2δ = ε
( 2 x – 1 – 7( x – 3))( 2 x – 1 + 7( x – 3))
⇔ <ε
x – 3( 2 x – 1 + 7( x – 3))
2 x – 1 – (7 x – 21)
⇔ <ε
x – 3( 2 x – 1 + 7( x – 3))
–5( x – 4)
⇔ <ε
x – 3( 2 x – 1 + 7( x – 3))
Instructor’s Resource Manual Section 1.2 69
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

8. ⇔ x−4 ⋅
5
<ε 10 x3 – 26 x 2 + 22 x – 6
19. 0 < x – 1 < δ ⇒ –4 <ε
x − 3( 2 x − 1 + 7( x − 3)) ( x – 1) 2
10 x3 – 26 x 2 + 22 x – 6
To bound
5
, agree that –4 <ε
x – 3( 2 x – 1 + 7( x – 3)) ( x –1)2
1 1 7 9 (10 x – 6)( x – 1)2
δ ≤ . If δ ≤ , then < x < , so ⇔ –4 <ε
2 2 2 2 ( x – 1)2
5 ⇔ 10 x – 6 – 4 < ε
0.65 < < 1.65 and
x – 3( 2 x – 1 + 7( x – 3))
⇔ 10( x – 1) < ε
5
hence x − 4 ⋅ <ε ⇔ 10 x – 1 < ε
x − 3( 2 x − 1 + 7( x − 3))
ε
ε ⇔ x –1 <
⇔ x–4 < 10
1.65
For whatever ε is chosen, let δ be the smaller of
ε
δ= ; 0 < x –1 < δ
1 ε 10
and .
2 1.65 10 x3 – 26 x 2 + 22 x – 6 (10 x – 6)( x – 1) 2
–4 = –4
⎧1 ε ⎫ ( x – 1) 2 ( x – 1) 2
δ = min ⎨ , ⎬, 0 < x – 4 < δ
⎩ 2 1. 65 ⎭ = 10 x − 6 − 4 = 10( x − 1)
2x −1 5 = 10 x − 1 < 10δ = ε
− 7 = x−4 ⋅
x −3 x − 3( 2 x − 1 + 7( x − 3))
< x – 4 (1.65) < 1. 65δ ≤ ε 20. 0 < x – 1 < δ ⇒ (2 x 2 + 1) – 3 < ε
1 1 ε
since δ = only when ≤ so 1.65δ ≤ ε .
2 2 1. 65 2 x2 + 1 – 3 = 2 x2 – 2 = 2 x + 1 x – 1
To bound 2 x + 2 , agree that δ ≤ 1 .
14 x 2 – 20 x + 6
18. 0 < x – 1 < δ ⇒ –8 < ε
x –1 x – 1 < δ implies
2x + 2 = 2x – 2 + 4
14 x 2 – 20 x + 6 2(7 x – 3)( x – 1)
–8 <ε ⇔ –8 <ε ≤ 2x – 2 + 4
x –1 x –1
<2+4=6
⇔ 2(7 x – 3) – 8 < ε
ε ⎧ ε⎫
⇔ 14( x – 1) < ε δ ≤ ; δ = min ⎨1, ⎬; 0 < x – 1 < δ
6 ⎩ 6⎭
⇔ 14 x – 1 < ε
(2 x + 1) – 3 = 2 x 2 – 2
2
ε
⇔ x –1 < ⎛ε ⎞
14 = 2x + 2 x −1 < 6 ⋅ ⎜ ⎟ = ε
⎝6⎠
ε
δ= ; 0 < x –1 < δ
14
14 x 2 – 20 x + 6 2(7 x – 3)( x – 1)
–8 = –8
x –1 x –1
= 2(7 x – 3) – 8
= 14( x – 1) = 14 x – 1 < 14δ = ε
70 Section 1.2 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

9. 21. 0 < x + 1 < δ ⇒ ( x 2 – 2 x – 1) – 2 < ε ⎛1⎞
25. For all x ≠ 0 , 0 ≤ sin 2 ⎜ ⎟ ≤ 1 so
⎝x⎠
x2 – 2 x – 1 – 2 = x2 – 2 x – 3 = x + 1 x – 3 ⎛ 1⎞
x 4 sin 2 ⎜ ⎟ ≤ x 4 for all x ≠ 0 . By Problem 18,
To bound x – 3 , agree that δ ≤ 1 . ⎝ x⎠
4
x + 1 < δ implies lim x = 0, so, by Problem 20,
x→0
x – 3 = x + 1 – 4 ≤ x + 1 + –4 < 1 + 4 = 5 4 2 ⎛ 1⎞
lim x sin ⎜ ⎟ = 0.
ε ⎧ ε⎫ x→0 ⎝ x⎠
δ ≤ ; δ = min ⎨1, ⎬ ; 0 < x + 1 < δ
5 ⎩ 5⎭
( x – 2 x – 1) – 2 = x 2 – 2 x – 3
2 26. 0 < x < δ ⇒ x –0 = x = x <ε
For x > 0, ( x ) = x.
2
ε
= x +1 x – 3 < 5⋅ =ε
5 x < ε ⇔ ( x )2 = x < ε 2
δ = ε 2; 0 < x < δ ⇒ x < δ = ε 2 = ε
22. 0 < x < δ ⇒ x 4 – 0 = x 4 < ε
x 4 = x x3 . To bound x3 , agree that 27. lim x : 0 < x < δ ⇒ x – 0 < ε
x →0 +
δ ≤ 1. x < δ ≤ 1 implies x3 = x ≤ 1 so
3 For x ≥ 0 , x = x .
δ = ε; 0 < x < δ ⇒ x – 0 = x = x < δ = ε
δ ≤ ε.
Thus, lim+ x = 0.
δ = min{1, ε }; 0 < x < δ ⇒ x 4 = x x3 < ε ⋅1 x→0
=ε lim x : 0 < 0 – x < δ ⇒ x – 0 < ε
x →0 –
23. Choose ε > 0. Then since lim f ( x) = L, there is For x < 0, x = – x; note also that x = x
x →c
some δ1 > 0 such that since x ≥ 0.
0 < x – c < δ1 ⇒ f ( x ) – L < ε . δ = ε ;0 < − x < δ ⇒ x = x = − x < δ = ε
Since lim f (x) = M, there is some δ 2 > 0 such Thus, lim– x = 0,
x→c x→0
that 0 < x − c < δ 2 ⇒ f ( x) − M < ε . since lim x = lim x = 0, lim x = 0.
Let δ = min{δ1 , δ2 } and choose x 0 such that x →0 + x →0 – x →0
0 < x0 – c < δ . 28. Choose ε > 0. Since lim g( x) = 0 there is some
Thus, f ( x0 ) – L < ε ⇒ −ε < f ( x0 ) − L < ε x→ a
δ1 > 0 such that
⇒ − f ( x0 ) − ε < − L < − f ( x0 ) + ε ε.
0 < x – a < δ1 ⇒ g(x ) − 0 <
⇒ f ( x0 ) − ε < L < f ( x0 ) + ε . B
Similarly, Let δ = min{1, δ1} , then f ( x) < B for
f ( x0 ) − ε < M < f ( x0 ) + ε . x − a < δ or x − a < δ ⇒ f ( x) < B. Thus,
Thus, x − a < δ ⇒ f ( x) g ( x) − 0 = f ( x) g ( x)
−2ε < L − M < 2ε . As ε ⇒ 0, L − M → 0, so
ε
L = M. = f ( x) g ( x) < B ⋅ = ε so lim f ( x)g(x) = 0.
B x→ a
24. Since lim G(x) = 0, then given any ε > 0, we
x→c
can find δ > 0 such that whenever
x – c < δ , G ( x) < ε .
Take any ε > 0 and the corresponding δ that
works for G(x), then x – c < δ implies
F ( x) – 0 = F ( x) ≤ G ( x ) < ε since
lim G(x) = 0.
x→c
Thus, lim F( x) = 0.
x→c
Instructor’s Resource Manual Section 1.2 71
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

10. 29. Choose ε > 0. Since lim f ( x) = L, there is a 1.3 Concepts Review
x→ a
δ > 0 such that for 0 < x – a < δ , f ( x) – L < ε . 1. 48
That is, for
2. 4
a − δ < x < a or a < x < a + δ ,
L − ε < f ( x) < L + ε . 3. – 8; – 4 + 5c
Let f(a) = A,
M = max { L − ε , L + ε , A } , c = a – δ, 4. 0
d = a + δ. Then for x in (c, d), f ( x) ≤ M , since
either x = a, in which case
Problem Set 1.3
f ( x) = f (a ) = A ≤ M or 0 < x – a < δ so 1. lim (2 x + 1) 4
x→1
L − ε < f ( x) < L + ε and f ( x) < M .
= lim 2 x + lim 1 3
x→1 x→1
30. Suppose that L > M. Then L – M = α > 0. Now = 2 lim x + lim 1 2,1
α x →1 x→1
take ε < and δ = min{δ1 , δ 2} where = 2(1) + 1 = 3
2
0 < x – a < δ1 ⇒ f ( x) – L < ε and 2. lim (3x 2 – 1) 5
x→ –1
0 < x – a < δ 2 ⇒ g ( x) – M < ε .
= lim 3x 2 – lim 1 3
Thus, for 0 < x – a < δ , x→ –1 x→–1
= 3 lim x 2 – lim 1 8
L – ε < f(x) < L + ε and M – ε < g(x) < M + ε. x→ –1 x→–1
Combine the inequalities and use the fact ⎛ ⎞
2
that f ( x) ≤ g ( x) to get = 3⎜ lim x ⎟ – lim 1 2, 1
⎝ x→ –1 ⎠ x →–1
L – ε < f(x) ≤ g(x) < M + ε which leads to 2
= 3(–1) – 1 = 2
L – ε < M + ε or L – M < 2ε.
However, 3. lim [(2 x +1)( x – 3)] 6
L – M = α > 2ε x→0
which is a contradiction. = lim (2 x +1) ⋅ lim (x – 3) 4, 5
x→ 0 x→ 0
Thus L ≤ M .
⎛ ⎞ ⎛ ⎞
= ⎜ lim 2 x + lim 1⎟ ⋅ ⎜ lim x – lim 3⎟ 3
31. (b) and (c) are equivalent to the definition of ⎝ x→ 0 x→ 0 ⎠ ⎝ x→0 x→ 0 ⎠
limit. ⎛ ⎞ ⎛ ⎞
= ⎜ 2 lim x + lim 1⎟ ⋅ ⎜ lim x – lim 3⎟ 2, 1
⎝ x →0 x→ 0 ⎠ ⎝ x→0 x→ 0 ⎠
32. For every ε > 0 and δ > 0 there is some x with
= [2(0) +1](0 – 3) = –3
0 < x – c < δ such that f ( x ) – L > ε .
4. lim [(2 x 2 + 1)(7 x 2 + 13)] 6
x 3 – x 2 – 2x – 4 x→ 2
33. a. g(x) =
x 4 – 4x 3 + x 2 + x + 6 = lim (2 x 2 + 1) ⋅ lim (7 x 2 + 13) 4, 3
x→ 2 x→ 2
x+6 ⎛ ⎞ ⎛ ⎞
b. No, because + 1 has = ⎜ 2 lim x 2 + lim 1⎟ ⋅ ⎜ 7 lim x 2 + lim 13 ⎟ 8,1
x – 4x + x 2 + x + 6
4 3
⎝ x→ 2 x→ 2 ⎠ ⎝ x→ 2 x→ 2 ⎠
an asymptote at x ≈ 3.49.
⎡ ⎛ ⎞
2 ⎤⎡ ⎛ ⎞
2 ⎤
= ⎢2⎜ lim x ⎟ + 1⎥ ⎢7⎜ lim x ⎟ + 13⎥ 2
1 ⎢ ⎝ x→ 2 ⎠ ⎥⎢ ⎝ x→ 2 ⎠ ⎥
c. If δ ≤ , then 2.75 < x < 3 ⎣ ⎦⎣ ⎦
4
or 3 < x < 3.25 and by graphing = [2( 2 ) 2 + 1][7( 2 ) 2 + 13] = 135
x3 − x 2 − 2 x − 4
y = g ( x) =
x 4 − 4 x3 + x 2 + x + 6
on the interval [2.75, 3.25], we see that
x3 – x 2 – 2 x – 4
0< <3
x 4 – 4 x3 + x 2 + x + 6
so m must be at least three.
72 Section 1.3 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

11. 2x + 1 9. lim (2t 3 +15)13 8
5. lim 7 t→ –2
x→2 5 – 3x 13
⎡ ⎤
lim (2 x + 1) = ⎢ lim (2t3 + 15) ⎥ 4, 3
= x→2 4, 5 ⎣t→–2 ⎦
lim (5 – 3 x) 13
⎡ ⎤
x→2
= ⎢2 lim t 3 + lim 15⎥ 8
lim 2 x + lim 1 ⎣ t→ –2 t→ –2 ⎦
x→2 x→2
= 3, 1 13
lim 5 – lim 3 x ⎡ 3 ⎤
x→2 x→2 = ⎢ 2 ⎛ lim t ⎞ + lim 15⎥
⎜ ⎟ 2, 1
2 lim x + 1 ⎢ ⎝ t → –2 ⎠ t → –2 ⎥
⎣ ⎦
x→2
= 2 = [2(–2) 3 + 15]13 = –1
5 – 3 lim x
x→2
2(2) + 1 lim –3w3 + 7 w2 9
= = –5 10.
w→ –2
5 – 3(2 )
= lim (–3w3 + 7 w2 ) 4, 3
3 w→ –2
4x +1
6. lim 7
x → –3 7 – 2 x 2 = –3 lim w3 + 7 lim w2 8
3 w→ –2 w→ –2
lim (4 x + 1)
= x → –3
4, 5 3 2
lim (7 – 2 x ) 2 = –3 ⎛ lim w ⎞ + 7 ⎛ lim w ⎞
⎜ ⎟ ⎜ ⎟ 2
x → –3 ⎝ w→ –2 ⎠ ⎝ w→ –2 ⎠
lim 4 x 3 + lim 1 = –3(–2)3 + 7(–2) 2 = 2 13
x → –3 x → –3
= 3, 1
lim 7 – lim 2 x 2
x → –3 x → –3 1/ 3
⎛ 4 y3 + 8 y ⎞
4 lim x 3 + 1 11. lim ⎜ ⎟ 9
= x → –3
8 y →2 ⎜ y + 4 ⎟
⎝ ⎠
7 – 2 lim x 2
x → –3 1/ 3 7
⎛ 4 y3 + 8 y ⎞
3 = ⎜ lim ⎟
4⎛ lim x ⎞ + 1
⎜ ⎟ ⎜ y →2 y + 4 ⎟
⎝ ⎠
= ⎝
x → –3 ⎠
2
2 13
7 – 2⎛ lim x ⎞ ⎡ lim (4 y 3 + 8 y ) ⎤
⎜ ⎟ ⎢ y →2 ⎥
⎝ x → –3 ⎠ =⎢ 4, 3
⎥
=
4(–3)3 + 1 107
= ⎢ y →2( y + 4) ⎥
lim
⎣ ⎦
7 – 2(–3) 2 11
13
⎛ 4 lim y 3 + 8 lim y ⎞
7. lim 3 x – 5 9 ⎜ y →2 y →2 ⎟
x →3
=⎜ ⎟ 8, 1
⎜ y →2 y + y → 2 4 ⎟
lim lim
= lim (3 x – 5) 5, 3 ⎝ ⎠
x →3
1/ 3
= 3 lim x – lim 5 2, 1 ⎡ ⎛ ⎞
3 ⎤
x →3 x →3 ⎢ 4 ⎜ lim y ⎟ + 8 lim y ⎥
⎢ y →2 ⎠ y →2 ⎥
= 3(3) – 5 = 2 =⎢ ⎝ ⎥ 2
lim y + 4
⎢ y →2 ⎥
⎢ ⎥
8. lim 5x2 + 2 x 9 ⎣ ⎦
x → –3 1/ 3
⎡ 4(2)3 + 8(2) ⎤
= 2
lim (5 x + 2 x ) 4, 3 =⎢ ⎥ =2
x → –3 ⎢
⎣ 2+4 ⎥
⎦
= 5 lim x 2 + 2 lim x 8
x → –3 x → –3
2
= 5 ⎛ lim x ⎞ + 2 lim x
⎜ ⎟ 2
⎝ x→ –3 ⎠ x → –3
= 5(–3)2 + 2(–3) = 39
Instructor’s Resource Manual Section 1.3 73
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

12. 12. lim (2 w 4 – 9 w 3 +19)–1 /2 x 2 + 7 x + 10 ( x + 2)( x + 5)
w→ 5 18. lim = lim
1
x→2 x+2 x→2 x+2
= lim 7 = lim( x + 5) = 7
w→ 5 2w − 9 w3 + 19
4 x→2
lim 1
= w→5
1, 9 x2 + x − 2 ( x + 2)( x − 1)
4 3 19. lim = lim
lim 2w – 9 w + 19 x →1 x −12 x →1 ( x + 1)( x − 1)
w→ 5
1 x + 2 1+ 2 3
= lim = =
= 4,5 x →1 x + 1 1+1 2
lim (2w – 9 w3 + 19)
4
w→ 5
x 2 – 14 x – 51 ( x + 3)( x – 17)
1 20. lim = lim
= 1,3 2
x→ –3 x – 4 x – 21 x→ –3 ( x + 3)( x – 7)
lim 2 w4 − lim 9 w3 + lim 19 x – 17 –3 – 17
w→5 w→5 w→5 = lim = =2
x→ –3 x – 7 –3 – 7
1
= 8
2 lim w − 9 lim w3 + 19
4 u2 – ux + 2u – 2 x ( u + 2 )( u – x )
w→5 w→5 21. lim 2 = lim
u →–2 u –u– 6 u→ –2 ( u + 2)(u – 3)
1 u– x x+2
= 2 = lim =
4 3
u → –2 u – 3 5
2 ⎛ lim w ⎞ − 9 ⎛ lim w ⎞ + 19
⎜ ⎟ ⎜ ⎟
⎝ w→ 5 ⎠ ⎝ w→5 ⎠
x 2 + ux – x – u ( x – 1)( x + u)
1 22. lim = lim
= x→1 x 2 + 2x – 3 x →1 ( x – 1)( x + 3)
2(5)4 − 9(5)3 + 19 x + u 1+ u u + 1
= lim = =
1 1 x→1 x + 3 1+ 3 4
= =
144 12
2 x2 – 6 xπ + 4 π2 2( x – π)( x – 2 π)
23. lim = lim
x2 − 4 (
lim x − 4
x→2
2
) 4−4 x→ π x –π 2 2
x→ π ( x – π)( x + π)
2( x – 2π) 2(π – 2 π)
13. lim = = =0
lim ( x + 4) 4 + 4 = lim = = –1
2
x→2 x +4 2
x→ π x + π π+π
x→2
(w + 2)(w 2 – w – 6)
x2 − 5x + 6 ( x − 3)( x − 2 ) 24. lim
14. lim = lim w 2 + 4w + 4
x→2 x−2 x→2 ( x − 2) w→ –2
( w + 2) 2 ( w – 3)
= lim ( x − 3) = −1 = lim = lim ( w – 3)
x→2 w→ –2 ( w + 2 )2 w→ –2
= –2 – 3 = –5
x2 − 2 x − 3 ( x − 3)( x + 1)
15. lim = lim
x →−1 x +1 x →−1 ( x + 1) 25. lim f 2 ( x) + g 2 ( x)
x→a
= lim ( x − 3) = −4
x →−1 = lim f 2 ( x) + lim g 2 ( x)
x→a x→a
x2 + x (
lim x + x
x →−1
2
) 0 2
= ⎛ lim f ( x) ⎞ + ⎛ lim g ( x) ⎞
⎜ ⎟ ⎜ ⎟
2
16. lim = = =0
x →−1 x2 + 1 lim ( x 2
+ 1) 2 ⎝ x →a ⎠ ⎝ x→a ⎠
x →−1
= (3) 2 + (–1)2 = 10
( x − 1)( x − 2)( x − 3) x−3
17. lim = lim
x →−1 ( x − 1)( x − 2)( x + 7) x →−1 x + 7 2 f ( x) – 3g ( x ) x → a[2 f ( x) – 3 g ( x)]
lim
26. lim =
−1 − 3 2 x → a f ( x) + g ( x) lim [ f ( x) + g ( x)]
= =− x→a
−1 + 7 3 2 lim f ( x) – 3 lim g ( x)
x→a x→a 2(3) – 3(–1) 9
= = =
lim f ( x) + lim g ( x) 3 + (–1) 2
x→a x→a
74 Section 1.3 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

13. 27. lim 3 g ( x) [ f ( x) + 3] = lim 3 g ( x) ⋅ lim [ f ( x) + 3] 35. Suppose lim f (x) = L and lim g(x) = M.
x→a x→a x→a x→c x→c
f ( x) g ( x) – LM ≤ g ( x) f ( x) – L + L g ( x ) – M
= 3 lim g ( x) ⋅ ⎡ lim f ( x) + lim 3⎤ = 3 – 1 ⋅ (3 + 3)
x→a ⎢x→a
⎣ x→a ⎥⎦ as shown in the text. Choose ε 1 = 1. Since
= –6 lim g ( x) = M , there is some δ1 > 0 such that if
x →c
4 0 < x – c < δ1 , g ( x) – M < ε1 = 1 or
28. lim [ f ( x) – 3]4 = ⎡ lim ( f ( x) – 3) ⎤
⎢ x→a ⎥
x→a ⎣ ⎦ M – 1 < g(x) < M + 1
4
= ⎡ lim f ( x) – lim 3⎤ = (3 – 3) 4 = 0
⎢ x→a
M – 1 ≤ M + 1 and M + 1 ≤ M + 1 so for
⎣ x →a ⎥
⎦
0 < x – c < δ1 , g ( x) < M + 1. Choose ε > 0.
29. lim ⎡ f (t ) + 3g (t ) ⎤ = lim f (t ) + 3 lim g (t ) Since lim f (x) = L and lim g(x) = M, there
t →a
⎣ ⎦ t →a t →a x→c x→c
exist δ 2 and δ 3 such that 0 < x – c < δ 2 ⇒
= lim f (t ) + 3 lim g (t )
t →a t →a ε
f ( x) – L < and 0 < x – c < δ 3 ⇒
= 3 + 3 –1 = 6 L + M +1
ε
⎛ ⎞
3 g ( x) – M < . Let
3
30. lim [ f (u) + 3g(u)] = ⎜ lim [ f (u) + 3g(u)]⎟ L + M +1
u →a ⎝ u →a ⎠
3 δ = min{δ1 , δ 2 , δ 3 }, then 0 < x – c < δ ⇒
⎡ ⎤
= ⎢ lim f (u ) + 3 lim g(u) ⎥ = [3 + 3( –1)]3 = 0 f ( x) g ( x) – LM ≤ g ( x) f ( x) – L + L g ( x ) – M
⎣u→ a u →a ⎦
ε ε
< ( M + 1) +L =ε
3x 2
– 12 3( x – 2 )(x + 2) L + M +1 L + M +1
31. lim = lim
x→2 x–2 x→2 x –2 Hence,
= 3 lim (x + 2) = 3(2 + 2) = 12
x→2 lim f ( x) g ( x) = LM = ⎛ lim f ( x) ⎞ ⎛ lim g ( x) ⎞
⎜ ⎟⎜ ⎟
x →c ⎝ x →c ⎠ ⎝ x →c ⎠
(3x 2 + 2 x + 1) – 17 3x 2 + 2 x – 16
32. lim
x→2 x–2
= lim
x →2 x–2 36. Say lim g ( x ) = M , M ≠ 0 , and choose
x →c
(3 x + 8)( x – 2) 1
= lim = lim (3 x + 8) ε1 = M
x→2 x–2 x →2 2 .
= 3 lim x + 8 = 3(2) + 8 = 14 There is some δ1 > 0 such that
x→2
1
0 < x − c < δ1 ⇒ g ( x) − M < ε1 = M or
1
– 1 2– x
– x–2 2
2 2x 2x
33. lim x
= lim = lim 1 1
x→2 x – 2 x→2 x – 2 x →2 x – 2 M− M < g ( x) < M + M .
2 2
1 –1 –1 1
= lim – = = =– 1 1 1 1
x→2 2 x 2 lim x 2(2) 4 M − M ≥ M and M + M ≥ M
x →2 2 2 2 2
1 1 2
3 3 3( 4 – x 2 ) –3( x + 2 )( x – 2 ) so g ( x) > M and <
– 4 2 g ( x) M
x2 4x2 4x2
34. lim = lim = lim
x→2 x–2 x–2 x→2
x→2 x–2 Choose ε > 0.
Since lim g(x) = M there is δ 2 > 0 such that
–3 ⎛ lim x + 2 ⎞
⎜ ⎟ –3(2 + 2) x→c
–3( x + 2)
= lim = ⎝ x →2 ⎠= 1 2
x→2 4x 2 2
4(2)2 0 < x − c < δ 2 ⇒ g ( x) − M < M .
4 ⎛ lim x ⎞
⎜ ⎟ 2
⎝ x→2 ⎠ Let δ = min{δ1 , δ 2}, then
3
=– 1 1 M – g ( x)
4 0< x–c <δ ⇒ – =
g ( x) M g ( x) M
1 2 2 1 2
= g ( x) − M < g ( x) − M = ⋅ M ε
2
M g ( x) M M2 2
=ε
Instructor’s Resource Manual Section 1.3 75
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

14. 1 1 1
Thus, lim = = . x–3 ( x – 3) x 2 – 9
x→c g(x) M lim g (x) 43. lim = lim
x→c x →3+ x2 – 9 x →3+ x2 – 9
Using statement 6 and the above result,
f ( x) 1 ( x – 3) x 2 – 9 x2 – 9
lim = lim f ( x) ⋅ lim = lim = lim
x →c g ( x ) x →c x →c g ( x ) x →3+ ( x – 3)( x + 3) x →3+ x+3
lim f ( x ) 32 – 9
1
= lim f ( x) ⋅ = x →c . = =0
x →c lim g ( x ) lim g ( x) 3+3
x →c x →c
1+ x 1+1 2
37. lim f (x) = L ⇔ lim f ( x) = lim L 44. lim = =
x→c x→ c x→ c x →1– 4 + 4 x 4 + 4(1) 8
⇔ lim f (x) – lim L = 0
x→c x →c
⇔ lim [ f (x) – L] = 0 ( x 2 + 1) x (22 + 1) 2 5⋅ 2 2
x→c 45. lim = = =
2 2 2
x → 2+ (3 x − 1) (3 ⋅ 2 − 1) 5 5
2
⎡ ⎤
38. lim f (x) = 0 ⇔ ⎢ lim f (x) ⎥ = 0
x→c ⎣ x→c ⎦ 46. lim ( x − x ) = lim x − lim x = 3− 2 =1
2 x →3− x →3− x →3−
⇔ lim f ( x) = 0
x→c
x
⇔ lim f 2 ( x) = 0 47. lim = –1
x →c x →0 – x
⇔ lim f 2 ( x) = 0
x →c 48. lim x 2 + 2 x = 32 + 2 ⋅ 3 = 15
⇔ lim f ( x) = 0 x →3+
x→c
1
2 49. f ( x) g ( x) = 1; g ( x) =
39. lim x = ⎛ lim x ⎞ = f ( x)
2
⎜ ⎟ lim x = lim x 2
x →c ⎝ x →c ⎠ x →c x →c 1
2
lim g ( x) = 0 ⇔ lim =0
x →a x →a f ( x)
= ⎛ lim x ⎞ = c 2 = c
⎜ ⎟
⎝ x →c ⎠ 1
⇔ =0
lim f ( x)
x +1 x–5 x→a
40. a. If f ( x) = , g ( x) = and c = 2, then No value satisfies this equation, so lim f ( x)
x–2 x–2 x→ a
lim [ f (x) + g (x)] exists, but neither must not exist.
x→c
lim f (x) nor lim g(x) exists. ⎛ x 1⎞
x→c x→c 50. R has the vertices ⎜ ± , ± ⎟
⎝ 2 2⎠
2 Each side of Q has length x 2 + 1 so the
b. If f ( x) = , g ( x) = x, and c = 0, then
x
lim [ f (x) ⋅ g( x)] exists, but lim f (x) does perimeter of Q is 4 x 2 + 1. R has two sides of
x 2 so the
x→c x→c
length 1 and two sides of length
not exist.
perimeter of R is 2 + 2 x 2 .
3+ x 3–3
41. lim = =0 perimeter of R 2 x2 + 2
x → –3+ x –3 lim = lim
x →0 + perimeter of Q x →0+ 4 x 2 + 1
π3 + x3 π3 + (– π)3 2 02 + 2 2 1
42. lim = =0 = = =
x → – π+ x –π 4 0 +12 4 2
76 Section 1.3 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

15. NO = (0 – 0)2 + (1 – 0)2 = 1 3 x tan x 3x (sin x / cos x) 3x
51. a. 4. lim = lim = lim
x →0 sin x x →0 sin x x → 0 cos x
OP = ( x – 0)2 + ( y – 0) 2 = x 2 + y 2 0
= =0
= x2 + x 1
NP = ( x – 0)2 + ( y – 1)2 = x 2 + y 2 – 2 y + 1 sin x 1 sin x 1 1
5. lim = lim = ⋅1 =
2
= x + x − 2 x +1
x →0 2x 2 x →0 x 2 2
MO = (1 – 0) 2 + (0 – 0) 2 = 1 sin 3θ 3 sin 3θ 3 sin 3θ
6. lim = lim ⋅ = lim
θ →0 2θ θ →0 2 3θ 2 θ →0 3θ
MP = ( x – 1)2 + ( y – 0) 2 = y2 + x2 – 2 x + 1
3 3
= ⋅1 =
= x2 − x + 1 2 2
perimeter of ΔNOP
lim sin 3θ sin 3θ cos θ sin 3θ
x →0+ perimeter of ΔMOP 7. lim = lim sin θ = lim
θ → 0 tan θ θ →0 θ →0 sin θ
cos θ
1 + x2 + x + x2 + x – 2 x + 1
= lim ⎡ sin 3θ 1 ⎤
x → 0+ 1 + x2 + x + x2 – x + 1 = lim ⎢cos θ ⋅ 3 ⋅ ⋅ sin θ ⎥
θ →0⎢
⎣ 3θ θ ⎥ ⎦
1+ 1
= =1 ⎡ sin 3θ 1 ⎤
1+ 1 = 3 lim ⎢cos θ ⋅ ⋅ sin θ ⎥ = 3 ⋅1 ⋅1 ⋅1 = 3
θ →0 ⎢
⎣ 3θ θ ⎥
⎦
1 x
b. Area of ΔNOP = (1)( x) =
2 2 sin 5θ
tan 5θ sin 5θ
1 x 8. lim = lim cos 5θ = lim
Area of ΔMOP = (1)( y ) = θ → 0 sin 2θ θ → 0 sin 2θ θ → 0 cos 5θ sin 2θ
2 2 ⎡ 1 sin 5θ 1 2θ ⎤
= lim ⎢ ⋅5⋅ ⋅ ⋅
5θ 2 sin 2θ ⎥
x
area of ΔNOP x θ →0 ⎣ cos 5θ ⎦
lim = lim 2 = lim
x →0 + area of ΔMOP x →0+ x x →0 + x 5 ⎡ 1 sin 5θ 2θ ⎤
2 = lim ⎢ ⋅ ⋅
2 θ →0 ⎣ cos 5θ 5θ sin 2θ ⎥ ⎦
= lim x =0 5 5
x →0+ = ⋅1⋅1⋅1 =
2 2
cos πθ
1.4 Concepts Review cot πθ sin θ sin πθ
sin θ
9. lim = lim
θ →0 2 sec θ θ →0 2
cos θ
1. 0
cos πθ sin θ cos θ
= lim
2. 1 θ →0 2sin πθ
⎡ cos πθ cos θ sin θ 1 πθ ⎤
3. the denominator is 0 when t = 0 . = lim ⎢ ⋅ ⋅ ⋅
θ →0 ⎣ 2 θ π sin πθ ⎥⎦
4. 1 1 ⎡ sin θ πθ ⎤
= lim cos πθ cos θ ⋅ ⋅
2 π θ →0 ⎢⎣ θ sin πθ ⎥
⎦
1 1
Problem Set 1.4 = ⋅1⋅1⋅1⋅1 =
2π 2π
cos x 1 sin 2 3t 9t sin 3t sin 3t
1. lim = =1 10. lim = lim ⋅ ⋅ = 0 ⋅1 ⋅1 = 0
x →0 x + 1 1 t →0 2t t →0 2 3t 3t
π
2. lim θ cosθ = ⋅0 = 0 tan 2 3t sin 2 3t
θ →π / 2 2 11. lim = lim
t →0 2t t →0 (2t )(cos 2 3t )
cos 2 t cos 2 0 1 3(sin 3t ) sin 3t
3. lim = = =1 = lim ⋅ = 0 ⋅1 = 0
t →0 1 + sin t 1 + sin 0 1 + 0
t →0 2 cos 2 3t 3t
tan 2t 0
12. lim = =0
t → 0 sin 2t − 1 −1
Instructor’s Resource Manual Section 1.4 77
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

16. sin(3t ) + 4t ⎛ sin 3t 4t ⎞ sin x
13. lim = lim ⎜ + ⎟ 19. lim 1 + =2
t →0 t sec t t →0 ⎝ t sec t t sec t ⎠ x →0 x
sin 3t 4t
= lim + lim
t →0 t sec t t →0 t sec t
sin 3t
= lim 3cos t ⋅ + lim 4 cos t
t →0 3t t →0
= 3 ⋅1 + 4 = 7
20. The result that lim cos t = 1 was established in
sin 2 θ sin θ sin θ t →0
14. lim = lim
θ →0 θ 2 θ →0 θ θ the proof of the theorem. Then
sin θ sin θ lim cos t = lim cos(c + h)
= lim × lim = 1× 1 = 1 t →c h →0
θ →0 θ θ →0 θ = lim (cos c cos h − sin c sin h)
h →0
15. lim x sin (1/ x ) = 0 = lim cos c lim cos h − sin c lim sin h
x →0 h →0 h →0 h→0
= cos c
lim sin t
sin t t →c sin c
21. lim tan t = lim = = = tan c
t →c t → c cos t lim cos t cos c
t →c
lim cos t
cos t t →c cos c
lim cot t = lim = = = cot c
t →c t →c sin t lim sin t sin c
t →c
( )
1 1
16. lim x sin 1/ x 2 = 0 22. lim sec t = lim = = sec c
x →0 t →c cos t cos c
t →c
1 1
lim csc t = lim = = csc c
t →c t →c sin t sin c
23. BP = sin t , OB = cos t
area( ΔOBP) ≤ area (sector OAP)
≤ area (ΔOBP) + area( ABPQ)
1 1 1
OB ⋅ BP ≤ t (1) 2 ≤ OB ⋅ BP + (1 – OB ) BP
2 2 2
(
17. lim 1 − cos 2 x / x = 0
x →0
) 1
2
1 1
sin t cos t ≤ t ≤ sin t cos t + (1 – cos t ) sin t
2 2
t
cos t ≤ ≤ 2 – cos t
sin t
1 sin t 1 π π
≤ ≤ for − < t < .
2 – cos t t cos t 2 2
1 sin t 1
lim ≤ lim ≤ lim
t →0 2 – cos t t →0 t t →0 cos t
sin t
1 ≤ lim ≤1
t →0 t
18. lim cos 2 x = 1
x →0 sin t
Thus, lim = 1.
t →0 t
78 Section 1.4 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

17. Written response
x2
24. a.
1
6. lim = lim =1
1 1 x→∞x 2 – 8 x + 15 x → ∞ 1 – 8 + 15
b. D= AB ⋅ BP = (1 − cos t ) sin t x x2
2 2
sin t (1 − cos t )
= x3 1 1
2 7. lim 3 2
= lim =
1 1 t sin t cos t
x →∞ 2 x – 100 x x →∞ 2 – 100 2
E = t (1)2 – OB ⋅ BP = –
x
2 2 2 2
D sin t (1 – cos t ) πθ 5 π
= 8. lim = lim =π
E t – sin t cos t θ → – ∞ θ 5 – 5θ 4 θ →–∞ 1 – 5
θ
⎛D⎞
c. lim ⎜ ⎟ = 0.75
3 x3 – x 2 3– 1 3
+⎝ E ⎠ x =
t →0 9. lim = lim
x → ∞ πx 3 – 5x2 x → ∞ π – 5 π
x
1.5 Concepts Review sin 2 θ
10. lim ; 0 ≤ sin 2 θ ≤ 1 for all θ and
θ →∞ θ 2 – 5
1. x increases without bound; f(x) gets close to L as 1
x increases without bound 1 θ2 sin 2 θ
lim = lim = 0 so lim =0
θ →∞ θ 2 – 5 θ →∞ 1 – 5 θ →∞ θ 2 – 5
2. f(x) increases without bound as x approaches c θ2
from the right; f(x) decreases without bound as x
approaches c from the left 3 x3 + 3 x 3 x3 / 2 + 3 x
11. lim = lim
3. y = 6; horizontal x →∞ 2 x3 x →∞ 2 x3 / 2
3+ 3 3
4. x = 6; vertical
= lim x
=
x →∞ 2 2
Problem Set 1.5
πx3 + 3x πx3 + 3 x
12. lim 3 = 3 lim
1. lim
x
= lim
1
=1
x →∞ 2 x3 + 7 x x →∞ 2 x3 + 7 x
x →∞ x – 5 x →∞ 1 – 5 3
x π+ π
x2
= 3 lim =3
x →∞ 2 + 72 2
1
x2
x
2. lim = lim x
=0
x →∞ 5 – x3 x →∞ 5 –1 2 2
x3 1 + 8x 1 + 8x
13. lim 3 = 3 lim
2
x →∞ x + 4 x →∞ x 2 + 4
t2 1 1
3. lim = lim = −1 +8
t →–∞ 7 − t 2 t →–∞ 7 −1 x2
= 3 lim = 38 =2
t2 x →∞ 1 + 4
x2
t 1
4. lim = lim =1
t →–∞ t – 5 t →–∞ 1 – 5 x2 + x + 3 x2 + x + 3
t 14. lim = lim
x →∞ ( x –1)( x + 1) x →∞ x 2 –1
x2 x2 1+ 1 + 3
5. lim = lim x 2
x →∞ ( x – 5)(3 – x) x →∞ − x 2 + 8 x − 15 = lim x
= 1 =1
x →∞ 1– 1
2
1 x
= lim = –1
x → ∞ −1 + 8 − 15
x x2 n 1 1
15. lim = lim =
n →∞ 2n + 1 n→∞ 2 + 1 2
n
Instructor’s Resource Manual Section 1.5 79
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

18. n2 1 1 9y + 1
16. lim = lim = =1 9 y3 + 1 y2
n →∞ n2 + 1 n →∞ 1 1+ 0 23. lim = lim = –∞
1+ y→– ∞ y2 – 2 y + 2 y→–∞ 1 – 2+ 2
n2 y y2
n2 lim n ∞
17. lim = lim
n
= n →∞
= =∞ a0 x n + a1 x n –1 +…+ an –1 x + an
n →∞ n + 1 n →∞ 1 24. lim
1+ ⎛ 1 ⎞ 1+ 0 x →∞ b0 x n + b1 x n –1 +…+ bn –1 x + bn
lim 1 +
n n →∞ ⎜ n ⎟
⎝ ⎠ a1 an –1 an
a0 + + …+ +
x x n –1 xn a0
1 = lim =
x →∞ b1 bn –1 bn
n 0 b0 + + …+ + b0
18. lim = lim n = =0 x x n –1 xn
n →∞ n2 + 1 n →∞ 1 1+ 0
1+
n2 n 1 1
25. lim = lim = =1
n →∞ 2
n +1 n →∞ 1 1+ 0
1+ 2
19. For x > 0, x = x 2 . n
2x + 1 2+ 1 2+ 1
lim = lim x
= lim x
n2
x →∞ x →∞ x 2 +3 x →∞ 1+
x2 + 3 3
2
2 x2 n n3/ 2 ∞
x
26. lim = lim = =∞
2 n →∞ 3
n + 2n + 1 n →∞ 2 1 1
= =2 1+ 2 + 3
1 n n
+
2 x +1 2 + 1 27. As x → 4+ , x → 4 while x – 4 → 0 .
2x +1 xx2 x 2
20. lim = lim = lim =0 lim
x
=∞
x →∞ x+4 x →∞ 1 + 4 x →∞ 1 + 4 + x–4
x x x →4
21. lim ⎛ 2 x 2 + 3 – 2 x 2 – 5 ⎞
⎜ ⎟ 28. lim
t2 – 9
= lim
(t + 3)(t – 3)
x →∞ ⎝ ⎠ + t +3 + t +3
t → –3 t → –3
⎛ 2 x 2 + 3 – 2 x 2 – 5 ⎞⎛ 2 x 2 + 3 + 2 x 2 – 5 ⎞ = lim (t – 3) = –6
⎜ ⎟⎜ ⎟
= lim ⎝ ⎠⎝ ⎠ t → –3+
x →∞ 2
2x + 3 + 2x – 5 2
2 x 2 + 3 – (2 x 2 – 5) 29. As t → 3– , t 2 → 9 while 9 – t 2 → 0+.
= lim
x →∞ t2
2 x2 + 3 + 2 x2 – 5 lim =∞
8 t →3– 9 – t2
8
= lim = lim x
x →∞ 2 x + 3 + 2 x2 − 5
2 x →∞ 2 x 2 +3 + 2 x 2 –5 +
30. As x → 3 5 , x 2 → 52 / 3 while 5 – x3 → 0 – .
x2
x2
8 lim = –∞
= lim x =0 x→3 5
+
5 – x3
x →∞ 2+ 3 + 2– 5
x2 x2
31. As x → 5– , x 2 → 25, x – 5 → 0 – , and
22. 3 – x → –2.
lim ⎛ x 2 + 2 x − x ⎞
⎜ ⎟ lim
x2
=∞
x →∞ ⎝ ⎠
x →5 – ( x – 5)(3 – x)
⎛ x 2 + 2 x – x ⎞⎛ x 2 + 2 x + x ⎞
⎜ ⎟⎜ ⎟
= lim ⎝ ⎠⎝ ⎠ 32. As θ → π+ , θ 2 → π2 while sin θ → 0− .
x →∞ 2
x + 2x + x θ2
2
x + 2x – x 2
2x lim = −∞
= lim = lim θ →π+ sin θ
x →∞ x 2 + 2 x + x x→∞ x 2 + 2 x + x
2 2
= lim = =1
x →∞ 1+ 2 +1 2
x
80 Section 1.5 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

19. −
33. As x → 3− , x3 → 27, while x − 3 → 0 . 43. lim
3
= 0, lim
3
= 0;
x 3 x →∞ x +1 x→ – ∞ x + 1
lim = −∞ Horizontal asymptote y = 0.
x →3− x−3
3 3
lim = ∞, lim = – ∞;
x → –1+ x + 1 x → –1– x + 1
π+ π2
34. As θ → , πθ → while cos θ → 0 – . Vertical asymptote x = –1
2 2
πθ
lim = –∞
θ→ π + cos θ
2
x2 – x – 6 ( x + 2)( x – 3)
35. lim = lim
x →3– x–3 x →3– x–3
= lim ( x + 2) = 5
x →3 –
x2 + 2 x – 8 ( x + 4)( x – 2)
36. lim = lim
x → 2+ x –4 2
x → 2+ ( x + 2)( x – 2) 3 3
44. lim = 0, lim = 0;
x →∞ ( x + 1) 2 x → – ∞ ( x + 1) 2
x+4 6 3
= lim = =
x → 2+ x + 2 4 2 Horizontal asymptote y = 0.
3 3
lim = ∞, lim = ∞;
x x → –1+ ( x + 1) 2 x → –1– ( x + 1) 2
37. For 0 ≤ x < 1 , x = 0 , so for 0 < x < 1, =0
x Vertical asymptote x = –1
x
thus lim =0
x →0 + x
38. For −1 ≤ x < 0 , x = −1 , so for –1 < x < 0,
x 1 x
=− thus lim = ∞.
x x x →0 − x
1
(Since x < 0, – > 0. )
x
39. For x < 0, x = – x, thus
2x 2
x –x 45. lim = lim = 2,
lim = lim = –1 x →∞ x – 3 x→∞ 1 – 3
x →0 – x →0 –
x x x
2x 2
lim = lim = 2,
x x x →−∞ x – 3 x →−∞ 1 – 3
40. For x > 0, x = x, thus lim = lim =1 x
x →0 + x x →0 + x Horizontal asymptote y = 2
2x 2x
lim = ∞, lim = – ∞;
41. As x → 0 – , 1 + cos x → 2 while sin x → 0 – . x →3+ x – 3 x →3– x – 3
1 + cos x Vertical asymptote x = 3
lim = –∞
x →0 – sin x
42. –1 ≤ sin x ≤ 1 for all x, and
1 sin x
lim = 0, so lim = 0.
x →∞ x x →∞ x
Instructor’s Resource Manual Section 1.5 81
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

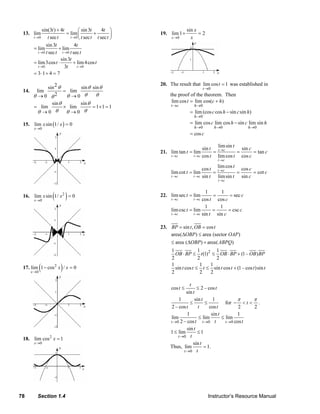
20. 3 3 1
46. lim = 0, lim = 0; 49. f ( x ) = 2 x + 3 – 3
, thus
x →∞ 9 – x 2 x→ – ∞ 9 – x 2 x –1
Horizontal asymptote y = 0 ⎡ 1 ⎤
lim [ f ( x) – (2 x + 3)] = lim ⎢ – ⎥=0
3 3 x →∞ 3
x →∞ ⎣ x –1 ⎦
lim = – ∞, lim = ∞,
x →3 + 9 – x2 x →3 – 9 – x2 The oblique asymptote is y = 2x + 3.
3 3
lim = ∞, lim = – ∞; 4x + 3
x → –3+ 9 – x
2
x → –3– 9 – x
2 50. f ( x) = 3x + 4 – , thus
x2 + 1
Vertical asymptotes x = –3, x = 3
⎡ 4x + 3⎤
lim [ f ( x) – (3 x + 4)] = lim ⎢ – ⎥
x →∞ x →∞ ⎣ x 2 + 1 ⎦
⎡ 4+ 3 ⎤
x x2 ⎥
= lim ⎢ – =0.
x →∞ ⎢ 1+ 1 ⎥
⎢
⎣ 2 ⎥
x ⎦
The oblique asymptote is y = 3x + 4.
51. a. We say that lim f ( x) = – ∞ if to each
x →c +
negative number M there corresponds a δ > 0
such that 0 < x – c < δ ⇒ f(x) < M.
14 14
47. lim = 0, lim = 0;
x →∞ 2 x+7 2 x→ – ∞ 2 x2 + 7 b. We say that lim f ( x) = ∞ if to each
Horizontal asymptote y = 0 x →c –
2
Since 2x + 7 > 0 for all x, g(x) has no vertical positive number M there corresponds a δ > 0
asymptotes. such that 0 < c – x < δ ⇒ f(x) > M.
52. a. We say that lim f ( x) = ∞ if to each
x →∞
positive number M there corresponds an
N > 0 such that N < x ⇒ f(x) > M.
b. We say that lim f ( x ) = ∞ if to each
x → –∞
positive number M there corresponds an
N < 0 such that x < N ⇒ f(x) > M.
53. Let ε > 0 be given. Since lim f ( x ) = A, there is
x →∞
2x 2 2 a corresponding number M1 such that
48. lim = lim = = 2, ε
x →∞ 2
x +5 x →∞ 1+ 5 1 x > M1 ⇒ f ( x) – A < . Similarly, there is a
x2 2
2x 2 2 ε
lim = lim = = –2 number M2 such that x > M 2 ⇒ g ( x) – B < .
x→ – ∞ x→ – ∞ – 1 2
x2 + 5 – 1+ 5
x2 Let M = max{M1 , M 2 } , then
Since x 2 + 5 > 0 for all x, g(x) has no vertical x > M ⇒ f ( x) + g ( x) – ( A + B)
asymptotes. = f ( x) – A + g ( x) – B ≤ f ( x) – A + g ( x) – B
ε ε
< =ε
+
2 2
Thus, lim [ f ( x) + g ( x)] = A + B
x →∞
54. Written response
82 Section 1.5 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

21. 55. a. lim sin x does not exist as sin x oscillates m0
x →∞ 56. lim− m(v) = lim− =∞
between –1 and 1 as x increases. v →c v →c 1 − v2 / c2
1
b. Let u = , then as x → ∞, u → 0+. 3x 2 + x +1 3
x 57. lim 2
=
x →∞ 2x –1 2
1
lim sin = lim sin u = 0
x →∞ x u →0 +
2 x 2 – 3x 2
58. lim =
1 2
c. Let u = , then as x → ∞, u → 0+. x→ – ∞ 5x + 1 5
x
1 1 sin u 3
lim x sin = lim sin u = lim =1 59. lim ⎛ 2 x 2 + 3x – 2 x 2 – 5 ⎞ = –
⎜ ⎟
x →∞ x u → 0+ u u →0 + u x→ – ∞ ⎝ ⎠ 2 2
1 2x +1 2
d. Let u = , then 60. lim =
x
3/ 2
x →∞ 3x 2 + 1 3
3/ 2 1 ⎛1⎞
lim x sin = lim+ ⎜ ⎟ sin u
x →∞ x u →0 ⎝ u ⎠ 10
⎛ 1⎞
⎡⎛ 1 ⎞⎛ sin u ⎞⎤ 61. lim ⎜ 1 + ⎟ =1
= lim+ ⎢⎜ ⎟⎜ x →∞ ⎝ x⎠
⎜ ⎟ ⎟⎥ = ∞
u → 0 ⎢⎝ u ⎠⎝ u ⎠ ⎥
⎣ ⎦
x
⎛ 1⎞
e. As x → ∞, sin x oscillates between –1 and 1, 62. lim ⎜1 + ⎟ = e ≈ 2.718
x →∞ ⎝ x⎠
1
while x –1/ 2 = → 0.
x
x2
–1/ 2
sin x = 0 ⎛ 1⎞
lim x 63. lim ⎜ 1 + ⎟ =∞
x →∞ x →∞ ⎝ x⎠
1
f. Let u = , then sin x
x ⎛ 1⎞
64. lim ⎜1 + ⎟ =1
⎛π 1⎞ ⎛π ⎞ x →∞ ⎝ x⎠
lim sin ⎜ + ⎟ = lim+ sin ⎜ + u ⎟
x→∞ ⎝ 6 x ⎠ u →0 ⎝ 6 ⎠
sin x – 3
π 1 65. lim = –1
= sin = x–3
6 2 x →3–
1 ⎛ 1⎞ sin x – 3
g. As x → ∞, x + → ∞, so lim sin ⎜ x + ⎟ 66. lim = –1
x x →∞ ⎝ x⎠
x →3– tan( x – 3)
does not exist. (See part a.)
⎛ 1⎞ 1 1 cos( x – 3)
h. sin ⎜ x + ⎟ = sin x cos + cos x sin 67. lim = –∞
⎝ x⎠ x x x →3– x–3
⎡ ⎛ 1⎞ ⎤
lim ⎢sin ⎜ x + ⎟ – sin x ⎥ cos x
x →∞ ⎣ ⎝ x⎠ ⎦ 68. lim = –1
x→ π
+ x– π2
⎡ ⎛ 1 ⎞ 1⎤ 2
= lim ⎢sin x ⎜ cos –1⎟ + cos x sin ⎥
x →∞ ⎣ ⎝ x ⎠ x⎦
1
1 1 lim (1 + x ) x = e ≈ 2.718
As x → ∞, cos → 1 so cos –1 → 0. 69.
x x x →0 +
1
From part b., lim sin = 0.
x →∞ x 70. lim (1 + x )1/ x = ∞
As x → ∞ both sin x and cos x oscillate x → 0+
between –1 and 1.
⎡ ⎛ 1⎞ ⎤ 71. lim (1 + x ) x = 1
lim ⎢sin ⎜ x + ⎟ – sin x ⎥ = 0. x →0+
x →∞ ⎣ ⎝ x⎠ ⎦
Instructor’s Resource Manual Section 1.5 83
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

22. 13. lim f (t ) = lim (3 – t ) = 0
1.6 Concepts Review t →3+ t →3+
lim f (t ) = lim (t – 3) = 0
1. lim f ( x) t →3 – t →3–
x →c
lim f (t ) = f (3); continuous
t →3
2. every integer
14. lim f (t ) = lim (3 – t )2 = 0
3. lim f ( x) = f (a); lim f ( x) = f (b)
t →3+ t →3+
x→a+ x →b –
lim f (t ) = lim (t 2 – 9) = 0
4. a; b; f(c) = W t →3– t →3 –
lim f (t ) = f (3); continuous
t →3
Problem Set 1.6 15. lim f ( x) = −2 = f (3); continuous
t →3
1. lim[( x – 3)( x – 4)] = 0 = f (3); continuous
x →3 16. g is discontinuous at x = –3, 4, 6, 8; g is left
continuous at x = 4, 8; g is right continuous at
2. lim ( x 2 – 9) = 0 = g (3); continuous x = –3, 6
x →3
17. h is continuous on the intervals
3 (−∞, −5), [ −5, 4] , (4, 6), [ 6,8] , (8, ∞)
3. lim and h(3) do not exist, so h(x) is not
x →3 x – 3
continuous at 3. x 2 – 49 ( x – 7)( x + 7)
18. lim = lim = lim ( x + 7)
x →7 x – 7 x →7 x–7 x →7
4. lim t – 4 and g(3) do not exist, so g(t) is not = 7 + 7 = 14
t →3
Define f(7) = 14.
continuous at 3.
t –3 2 x 2 –18 2( x + 3)( x – 3)
5. lim and h(3) do not exist, so h(t) is not 19. lim = lim
x →3 3 – x x →3 3– x
t →3t –3
continuous at 3. = lim[–2( x + 3)] = –2(3 + 3) = –12
x →3
Define f(3) = –12.
6. h(3) does not exist, so h(t) is not continuous at 3.
sin(θ )
7. lim t = 3 = f (3); continuous 20. lim =1
t →3 θ →0 θ
Define g(0) = 1
8. lim t – 2 = 1 = g (3); continuous
t →3
t –1 ( t –1)( t + 1)
21. lim = lim
9. h(3) does not exist, so h(t) is not continuous at 3. t →1 t –1 t →1 (t –1)( t + 1)
t –1 1 1
10. f(3) does not exist, so f(x) is not continuous at 3. = lim = lim =
–1)( t + 1)
t →1 (t t →1 t +1 2
t 3 – 27 (t – 3)(t 2 + 3t + 9) 1
11. lim = lim Define H(1) = .
t →3 t – 3 t →3 t –3 2
= lim(t 2 + 3t + 9) = (3)2 + 3(3) + 9 = 27 = r (3) x4 + 2 x2 – 3 ( x 2 –1)( x 2 + 3)
t →3 22. lim = lim
continuous x → –1 x +1 x → –1 x +1
( x + 1)( x – 1)( x 2 + 3)
12. From Problem 11, lim r (t ) = 27, so r(t) is not = lim
t →3 x → –1 x +1
continuous at 3 because lim r (t ) ≠ r (3). = lim [( x – 1)( x 2 + 3)]
t →3 x → –1
= (–1 – 1)[(–1)2 + 3] = –8
Define φ(–1) = –8.
84 Section 1.6 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

23. ⎛ x2 – 1 ⎞ ⎛ ( x – 1)( x + 1) ⎞
37.
23. lim sin ⎜ ⎟ = lim sin ⎜ ⎟
x → –1 ⎜ x + 1 ⎟ x→ –1 ⎝ x +1 ⎠
⎝ ⎠
= lim sin( x –1) = sin(–1 – 1) = sin(−2) = – sin 2
x → –1
Define F(–1) = –sin 2.
24. Discontinuous at x = π ,30
33 – x 2
25. f ( x) = 38.
(π – x)( x – 3)
Discontinuous at x = 3, π
26. Continuous at all points
27. Discontinuous at all θ = nπ + π where n is any
2
integer.
28. Discontinuous at all u ≤ −5
39.
29. Discontinuous at u = –1
30. Continuous at all points
1
31. G ( x) =
(2 – x)(2 + x)
Discontinuous on (−∞, −2] ∪ [2, ∞)
32. Continuous at all points since 40.
lim f ( x) = 0 = f (0) and lim f ( x) = 1 = f (1).
x →0 x →1
33. lim g ( x ) = 0 = g (0)
x →0
lim g ( x) = 1, lim g ( x) = –1
x →1+ x →1–
lim g(x ) does not exist, so g(x) is discontinuous
x→1
at x = 1.
34. Discontinuous at every integer
Discontinuous at all points except x = 0, because
1 lim f ( x ) ≠ f (c) for c ≠ 0 . lim f ( x ) exists only
35. Discontinuous at t = n + where n is any integer x →c x →c
2 at c = 0 and lim f ( x) = 0 = f (0) .
x →0
36.
41. Continuous.
42. Discontinuous: removable, define f (10) = 20
43. Discontinuous: removable, define f (0) = 1
44. Discontinuous: nonremovable.
45. Discontinuous, removable, redefine g (0) = 1
46. Discontinuous: removable, define F (0) = 0
Instructor’s Resource Manual Section 1.6 85
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

24. 47. Discontinuous: nonremovable. 52. Let f ( x) = x3 + 3 x − 2. f is continuous on [0, 1].
48. Discontinuous: removable, define f (4) = 4 f(0) = –2 < 0 and f(1) = 2 > 0. Thus, there is at
least one number c between 0 and 1 such that
49. The function is continuous on the intervals x 3 + 3x − 2 = 0.
( 0,1] , (1, 2], (2,3], … 53. Because the function is continuous on [ 0,2π ] and
Cost $ (cos 0)03 + 6sin 5 0 – 3 = –3 < 0,
0.72
(cos 2π)(2π)3 + 6sin 5 (2π) – 3 = 8π3 – 3 > 0, there
0.60 is at least one number c between 0 and 2π such
0.48 that (cos t )t 3 + 6sin 5 t – 3 = 0.
54. Let f ( x ) = x − 7 x + 14 x − 8 . f(x) is
0.36 3 2
0.24
continuous at all values of x.
0.12 f(0) = –8, f(5) = 12
Because 0 is between –8 and 12, there is at least
1 2 3 4 5
one number c between 0 and 5 such that
6
Length of call in minutes f ( x ) = x 3 − 7 x 2 + 14 x − 8 = 0 .
This equation has three solutions (x = 1,2,4)
50. The function is continuous on the intervals
[0, 200], (200,300], (300, 400], …
Cost $
80
60
40
20 55. Let f ( x ) = x − cos x. . f(x) is continuous at all
values of x ≥ 0. f(0) = –1, f(π/2) = π / 2
100 200 300 400 500 Because 0 is between –1 and π / 2 , there is at
Miles Driven
least one number c between 0 and π/2 such that
51. The function is continuous on the intervals f ( x ) = x − cos x = 0.
(0, 0.25], (0.25, 0.375], (0.375, 0.5], … The interval [0.6,0.7] contains the solution.
Cost $
4
3
2
1
56. Let f ( x) = x5 + 4 x3 – 7 x + 14
f(x) is continuous at all values of x.
0.25 0.5 0.75 1
f(–2) = –36, f(0) = 14
Miles Driven
Because 0 is between –36 and 14, there is at least
one number c between –2 and 0 such that
f ( x) = x5 + 4 x3 – 7 x + 14 = 0.
86 Section 1.6 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

25. 57. Suppose that f is continuous at c, so 63. Let f(x) be the difference in times on the hiker’s
lim f ( x) = f (c). Let x = c + t, so t = x – c, then watch where x is a point on the path, and suppose
x →c x = 0 at the bottom and x = 1 at the top of the
as x → c , t → 0 and the statement mountain.
lim f ( x) = f (c) becomes lim f (t + c ) = f (c). So f(x) = (time on watch on the way up) – (time
x →c t →0
on watch on the way down).
Suppose that lim f (t + c) = f (c) and let x = t + f(0) = 4 – 11 = –7, f(1) = 12 – 5 = 7. Since time is
t→ 0
c, so t = x – c. Since c is fixed, t → 0 means that continuous, f(x) is continuous, hence there is
x → c and the statement lim f (t + c) = f (c) some c between 0 and 1 where f(c) = 0. This c is
t →0 the point where the hiker’s watch showed the
becomes lim f ( x) = f (c) , so f is continuous at same time on both days.
x →c
c. ⎡ π⎤
64. Let f be the function on ⎢0, 2 ⎥ such that f(θ) is
⎣ ⎦
58. Since f(x) is continuous at c,
the length of the side of the rectangle which
lim f ( x) = f (c) > 0. Choose ε = f ( c ) , then
x →c makes angle θ with the x-axis minus the length of
there exists a δ > 0 such that the sides perpendicular to it. f is continuous on
0 < x − c < δ ⇒ f ( x) − f (c) < ε . ⎡ π⎤
⎢0, 2 ⎥ . If f(0) = 0 then the region is
⎣ ⎦
Thus, f ( x ) − f ( c ) > −ε = − f ( c ) , or f ( x ) > 0 . circumscribed by a square. If f(0) ≠ 0, then
Since also f ( c ) > 0 , f ( x ) > 0 for all x in ⎛π ⎞
observe that f (0) = − f ⎜ ⎟ . Thus, by the
(c − δ , c + δ ). ⎝2⎠
Intermediate Value Theorem, there is an angle
59. Let g(x) = x – f(x). Then, π
g(0) = 0 – f(0) = –f(0) ≤ 0 and g(1) = 1 – f(1) ≥ 0 θ 0 between 0 and such that f (θ 0 ) = 0.
2
since 0 ≤ f(x) ≤ 1 on [0, 1] . If g(0) = 0, then Hence, D can be circumscribed by a square.
f(0) = 0 and c = 0 is a fixed point of f. If g(1) = 0,
then f(1) = 1 and c = 1 is a fixed point of f. If 65. Yes, g is continuous at R .
neither g(0) = 0 nor g(1) = 0, then g(0) < 0 and
lim g ( r ) = = lim g ( r )
GMm
g(1) > 0 so there is some c in [0, 1] such that
r →R− R2 r →R+
g(c) = 0. If g(c) = 0 then c – f(c) = 0 or
f(c) = c and c is a fixed point of f. 66. No. By the Intermediate Value Theorem, if f
were to change signs on [a,b], then f must be
60. For f(x) to be continuous everywhere,
0 at some c in [a,b]. Therefore, f cannot
f(1) = a(1) + b = 2 and f(2) = 6 = a(2) + b
a+b=2 change sign.
2a + b = 6 67. a. f(x) = f(x + 0) = f(x) + f(0), so f(0) = 0. We
– a = –4 want to prove that lim f (x) = f (c), or,
x→c
a = 4, b = –2 equivalently, lim [ f (x) – f (c)] = 0. But
x→c
61. For x in [0, 1], let f(x) indicate where the string f(x) – f(c) = f(x – c), so
originally at x ends up. Thus f(0) = a, f(1) = b. lim[ f ( x) – f (c)] = lim f ( x – c). Let
f(x) is continuous since the string is unbroken. x →c x →c
Since 0 ≤ a, b ≤ 1 , f(x) satisfies the conditions of h = x – c then as x → c, h → 0 and
Problem 59, so there is some c in [0, 1] with lim f ( x – c) = lim f (h) = f (0) = 0. Hence
x →c h →0
f(c) = c, i.e., the point of string originally at c
lim f (x) = f (c) and f is continuous at c.
ends up at c. x→c
Thus, f is continuous everywhere, since c
62. The Intermediate Value Theorem does not imply was arbitrary.
the existence of a number c between –2 and 2
such that f (c ) = 0. The reason is that the b. By Problem 43 of Section 0.5, f(t) = mt for
all t in Q. Since g(t) = mt is a polynomial
function f ( x ) is not continuous on [ −2, 2] . function, it is continuous for all real
numbers. f(t) = g(t) for all t in Q, thus
f(t) = g(t) for all t in R, i.e. f (t ) = mt.
Instructor’s Resource Manual Section 1.6 87
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

26. 68. If f(x) is continuous on an interval then ⎡ 3 3⎤
lim f ( x) = f (c) for all points in the interval: Domain: ⎢ – , ⎥ ;
x →c ⎣ 4 4⎦
lim f ( x) = f (c) ⇒ lim f ( x) ⎧ 3 3⎫
Range: ⎨ – , 0, ⎬
x →c x →c ⎩ 4 4⎭
2
= lim f 2 ( x) = ⎛ lim f ( x) ⎞
⎜ ⎟ b. At x = 0
x →c ⎝ x →c ⎠
= ( f (c))2 = f (c ) 3 3
c. If x = 0, f ( x) = 0 , if x = – , f ( x) = – and
4 4
⎧ 1 if x ≥ 0
69. Suppose f ( x) = ⎨ . f(x) is 3 3 3 3
⎩−1 if x < 0 if x = , f ( x) = , so x = − , 0, are
4 4 4 4
discontinuous at x = 0, but g(x) = f ( x) = 1 is fixed points of f.
continuous everywhere.
70. a.
1.7 Chapter Review
Concepts Test
1. False. Consider f ( x ) = x at x = 2.
2. False: c may not be in the domain of f(x), or
it may be defined separately.
3. False: c may not be in the domain of f(x), or
it may be defined separately.
4. True. By definition, where c = 0, L = 0.
b. If r is any rational number, then any deleted
interval about r contains an irrational 5. False: If f(c) is not defined, lim f ( x ) might
1 x→c
number. Thus, if f (r ) = , any deleted 2
q x –4
exist; e.g., f ( x) = .
interval about r contains at least one point c x+2
1 1 x2 – 4
such that f (r ) – f (c) = – 0 = . Hence, f(–2) does not exist, but lim = −4.
q q x →−2 x + 2
lim f (x) does not exist.
x→r
x 2 − 25 ( x − 5)( x + 5)
If c is any irrational number in (0, 1), then as 6. True: lim = lim
x →5 x − 5 x →5 x−5
p p
x = → c (where is the reduced form = lim ( x + 5) = 5 + 5 = 10
q q x →5
of the rational number) q → ∞, so
7. True: Substitution Theorem
f ( x) → 0 as x → c. Thus,
lim f ( x) = 0 = f (c) for any irrational sin x
x →c 8. False: lim =1
x →0 x
number c.
71. a. Suppose the block rotates to the left. Using 9. False: The tangent function is not defined for
all values of c.
3
geometry, f ( x) = – . Suppose the block
4 sin x
rotates to the right. Using geometry, 10. True: If x is in the domain of tan x = ,
cos x
3
f ( x) = . If x = 0, the block does not rotate, then cos x ≠ 0 , and Theorem A.7
4 applies..
so f(x) = 0.
88 Section 1.7 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

27. 11. True: Since both sin x and cos x are 25. True: Choose ε = 0. 001 f (2) then since
continuous for all real numbers, by lim f ( x ) = f (2), there is some δ
Theorem C we can conclude that x→2
such that 0 < x − 2 < δ ⇒
f ( x) = 2 sin 2 x − cos x is also
f ( x ) − f (2) < 0. 001 f (2), or
continuous for all real numbers.
−0. 001 f (2 ) < f ( x ) − f (2 )
12. True. By definition, lim f ( x ) = f ( c ) . < 0.001f(2)
x →c Thus, 0.999f(2) < f(x) < 1.001f(2) and
f(x) < 1.001f(2) for 0 < x − 2 < δ .
13. True. 2 ∈ [1,3] Since f(2) < 1.001f(2), as f(2) > 0,
f(x) < 1.001f(2) on (2 − δ , 2 + δ ).
14. False: lim may not exist
x →0 − 26. False: That lim [ f ( x ) + g ( x )] exists does
x→c
15. False: Consider f ( x) = sin x. not imply that lim f ( x ) and
x→c
x–3
16. True. By the definition of continuity on an lim g( x ) exist; e.g., f ( x) = and
interval. x→c x+2
x+7
g ( x) = for c = −2 .
17. False: Since −1 ≤ sin x ≤ 1 for all x and x+2
1 sin x
lim = 0 , we get lim =0. 27. True: Squeeze Theorem
x →∞ x x →∞ x
28. True: A function has only one limit at a
18. False. It could be the case where
point, so if lim f ( x ) = L and
lim f ( x ) = 2 x→ a
x →−∞
lim f ( x ) = M , L = M
x→ a
19. False: The graph has many vertical
asymptotes; e.g., x = ± π/2, ± 3π/2, 29. False: That f(x) ≠ g(x) for all x does not
± 5π/2, … imply that lim f ( x) ≠ lim g ( x). For
x →c x →c
20. True: x = 2 ; x = –2 2
x +x–6
example, if f ( x) = and
x–2
21. True: As x → 1+ both the numerator and
5
denominator are positive. Since the g ( x) =x, then f(x) ≠ g(x) for all x,
numerator approaches a constant and 2
the denominator approaches zero, the but lim f ( x ) = lim g ( x ) = 5.
x→2 x→ 2
limit goes to + ∞ .
30. False: If f(x) < 10, lim f ( x ) could equal 10
22. False: lim f ( x) must equal f(c) for f to be x→2
x →c if there is a discontinuity point (2, 10).
continuous at x = c. For example,
– x3 + 6 x 2 − 2 x − 12
23. True: lim f ( x) = f ⎛ lim x ⎞ = f (c), so f is
⎜ ⎟
f ( x) =
x–2
< 10 for
x →c ⎝ x →c ⎠
continuous at x = c. all x, but lim f ( x) = 10.
x →2
x
24. True: lim = 1 = f ( 2.3) 31. True: lim f ( x) = lim f 2 ( x)
x →2.3 2 x →a x →a
2
= ⎡ lim f ( x) ⎤ = (b)2 = b
⎢ x→a ⎥
⎣ ⎦
32. True: If f is continuous and positive on
[a, b], the reciprocal is also
continuous, so it will assume all
1 1
values between and .
f ( a) f (b )
Instructor’s Resource Manual Section 1.7 89
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

28. Sample Test Problems x −1 1− x
14. lim = lim = −1 since x − 1 < 0 as
x →1− x −1 x →1− x −1
x−2 2−2 0
1. lim = = =0
x →2 x + 2 2+2 4 x → 1−
u 2 – 1 12 − 1 sin 5 x 5 sin 5 x
2. lim = =0 15. lim = lim
x →0 3 x x →0 3 5 x
u →1 u + 1 1+1
5 sin 5 x 5 5
= lim = ×1 =
u2 – 1 (u – 1)(u + 1) 3 x →0 5 x 3 3
3. lim = lim = lim (u + 1)
u →1 u – 1 u →1 u –1 u →1
1 − cos 2 x 2 1 − cos 2 x
=1+1=2 16. lim = lim
x →0 3x x →0 3 2x
u +1 u +1 1 2 1 − cos 2 x 2
4. lim = lim = lim ; = lim = ×0 = 0
u →1 u 2
–1 u →1 (u + 1)(u – 1) u →1 u – 1 3 x →0 2x 3
does not exist
1
1−
x –2 x −1 x = 1+ 0 = 1
1– 2 1 17. lim = lim
5. lim x
= lim x
= lim x →∞ x + 2 x →∞ 2 1+ 0
x→2 x 2 x →2 ( x – 2)( x + 2) x→2 x ( x + 2) 1+
–4 x
1 1
= =
2 (2 + 2 ) 8 1
18. Since −1 ≤ sin t ≤ 1 for all t and lim = 0 , we
t →∞ t
z2 – 4( z + 2)( z – 2) sin t
6. lim = lim get lim =0.
z →2 z 2
+z–6 z → 2 ( z + 3)( z
– 2) t →∞ t
z +2 2 + 2 4
= lim = =
z→ 2 z + 3 2 + 3 5 t+2
19. lim = ∞ because as t → 0, t + 2 → 4
sin x
t →2 ( t − 2 )2
tan x 1 while the denominator goes to 0 from the right.
7. lim = lim cos x
= lim
x → 0 sin 2 x x → 0 2 sin x cos x x → 0 2 cos 2 x
1 1 cos x
= 2
= 20. lim = ∞ , because as x → 0+ , cos x → 1
2 cos 0 2 x →0 + x
while the denominator goes to 0 from the right.
y3 – 1 ( y – 1)( y 2 + y + 1)
8. lim = lim −
y →1 y 2 –1 y →1 ( y – 1)( y + 1) 21. lim tan 2 x = ∞ because as x → (π / 4 ) ,
x →π / 4−
y 2 + y + 1 12 + 1 + 1 3
= lim = = −
2 x → (π / 2 ) , so tan 2 x → ∞.
y →1 y +1 1+1 2
1 + sin x
9. lim
x–4
= lim
( x – 2)( x + 2) 22. lim = ∞ , because as x → 0+ ,
x →0 + x
x→4 x –2 x →4 x –2
1 + sin x → 1 while the denominator goes to
= lim ( x + 2) = 4 + 2 = 4
x→4 0 from the right.
cos x 23. Preliminary analysis: Let ε > 0. We need to find
10. lim does not exist. a δ > 0 such that
x →0 x
0 <| x − 3 |< δ ⇒| ( 2 x + 1) − 7 |< ε .
x –x | 2 x − 6 |< ε ⇔ 2 | x − 3 |< ε
11. lim = lim = lim (–1) = –1
x →0 – x x →0 – x x →0 – ε ε
⇔| x − 3 |< . Choose δ = .
2 2
12. lim 4x = 2
x →(1/ 2)+ Let ε > 0. Choose δ = ε / 2. Thus,
13. lim ( t − t ) = lim t − lim t = 1 − 2 = −1 ( 2 x + 1) − 7 = 2 x − 6 = 2 x − 3 < 2 (ε / 2 ) = ε .
t →2 – t →2 – t →2–
90 Section 1.7 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

29. 24. a. f(1) = 0 28.
b. lim f ( x) = lim (1 – x) = 0
x →1+ x →1+
c. lim f ( x) = lim x = 1
x →1– x →1–
d. lim f ( x) = –1 because
x → –1
lim f ( x) = lim x3 = –1 and
x → –1– x → –1–
lim f ( x) = lim x = –1
x → –1+ x → –1+
29. a(0) + b = –1 and a(1) + b = 1
25. a. f is discontinuous at x = 1 because f(1) = 0, b = –1; a + b = 1
but lim f (x ) does not exist. f is a–1=1
x→1
a=2
discontinuous at x = –1 because f(–1) does
not exist.
30. Let f ( x) = x5 – 4 x3 – 3 x + 1
b. Define f(–1) = –1 f(2) = –5, f(3) = 127
Because f(x) is continuous on [2, 3] and
26. a. 0 < u – a < δ ⇒ g (u ) – M < ε f(2) < 0 < f(3), there exists some number c
between 2 and 3 such that f(c) = 0.
b. 0 < a – x < δ ⇒ f ( x) – L < ε
31. Vertical: None, denominator is never 0.
27. a. lim[2 f ( x) – 4 g ( x)] x x
x →3 Horizontal: lim = lim = 0 , so
= 2 lim f ( x) – 4 lim g ( x ) x →∞ x 2
+1 x →−∞ x 2 +1
x →3 x →3 y = 0 is a horizontal asymptote.
= 2(3) – 4(–2) = 14
32. Vertical: None, denominator is never 0.
x2 – 9
b. lim g ( x) = lim g ( x )( x + 3)
x →3 x – 3 x →3 x2 x2
Horizontal: lim = lim = 1 , so
= lim g ( x ) ⋅ lim ( x + 3) = –2 ⋅ (3 + 3) = –12 x →∞ x 2
+ 1 x →−∞ x 2 + 1
x →3 x →3
y = 1 is a horizontal asymptote.
c. g(3) = –2
x2
33. Vertical: x = 1, x = −1 because lim =∞
d. lim g ( f ( x)) = g ⎛ lim f ( x) ⎞ = g (3) = –2
⎜ ⎟ x →1+ x2 − 1
x →3 ⎝ x →3 ⎠
x2
and lim =∞
2 x →−1− x2 − 1
e. lim f ( x) – 8 g ( x)
x →3
2 x2 x2
= lim = 1 , so
= ⎡ lim f ( x) ⎤ – 8 lim g ( x)
Horizontal: lim
⎢ x →3 ⎥ x →∞ x 2
− 1 x→−∞ x 2 − 1
⎣ ⎦ x →3
y = 1 is a horizontal asymptote.
= (3) 2 – 8(–2) = 5
g ( x) – g (3) –2 – g (3) −2 − (−2)
f. lim = =
x →3 f ( x) 3 3
=0
Instructor’s Resource Manual Section 1.7 91
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

30. 34. Vertical: x = 2, x = −2 because 2. a. g ( 2 ) = 1/ 2
3 3
x x
lim = ∞ and lim =∞ b. g ( 2.1) = 1/ 2.1 ≈ 0.476
2 2
x → 2+ x −4 x →−2− x −4
x3 c. g ( 2.1) − g ( 2 ) = 0.476 − 0.5 = −0.024
Horizontal: lim = ∞ and
x →∞ x 2 −4
3 g ( 2.1) − g ( 2 ) −0.024
x d. = = −0.24
lim = −∞ , so there are no horizontal 2.1 − 2 0.1
x →−∞ x 2
−4
asymptotes. e. g ( a + h ) = 1/ ( a + h )
35. Vertical: x = ±π / 4, ± 3π / 4, ± 5π / 4,… because
−h
lim tan 2 x = ∞ and similarly for other odd f. g ( a + h ) − g ( a ) = 1/ ( a + h ) − 1/ a =
x →π / 4− a (a + h)
multiples of π / 4.
−h
Horizontal: None, because lim tan 2 x and g (a + h) − g (a) a (a + h) −1
x →∞ g. = =
lim tan 2 x do not exist. (a + h) − a h a (a + h)
x →−∞
g (a + h) − g (a) −1
36. Vertical: x = 0, because h. lim =
h→0 (a + h) − a a2
sin x 1 sin x
lim = lim =∞.
+ x2 + x x
x →0 x →0 3. a. F ( 2 ) = 2 ≈ 1.414
Horizontal: y = 0, because
b. F ( 2.1) = 2.1 ≈ 1.449
sin x sin x
lim = lim = 0.
x →∞ x2 x →−∞ x2 c. F ( 2.1) − F ( 2 ) = 1.449 − 1.414 = 0.035
Review and Preview Problems F ( 2.1) − F ( 2 ) 0.035
d. = = 0.35
2.1 − 2 0.1
1. a. f ( 2 ) = 22 = 4
e. F (a + h) = a + h
b. f ( 2.1) = 2.12 = 4.41
f. F (a + h) − F (a) = a + h − a
c. f ( 2.1) − f ( 2 ) = 4.41 − 4 = 0.41
F (a + h) − F (a) a+h − a
f ( 2.1) − f ( 2 ) g. =
d. =
0.41
= 4.1 ( a + h) − a h
2.1 − 2 0.1
F (a + h) − F (a) a+h − a
f ( a + h ) = ( a + h ) = a 2 + 2ah + h 2 = lim
2
e. h. lim
h→0 (a + h) − a h→0 h
f ( a + h ) − f ( a ) = a 2 + 2ah + h 2 − a 2
= lim
( a+h − a )( a+h + a )
( )
f.
= 2ah + h 2 h →0 h a+h + a
a+h−a
f (a + h) − f (a) = lim
g.
(a + h) − a
=
2ah + h 2
h
= 2a + h h →0 h ( a+h + a )
h
= lim
h. lim
f (a + h) − f ( a)
= lim ( 2a + h ) = 2a
h →0 h ( a+h + a )
h→0 (a + h) − a h →0
1 1 a
= lim = =
h →0 a+h + a 2 a 2a
92 Review and Preview Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.

31. G ( 2) = ( 2) + 1 = 8 + 1 = 9
3 4 32π
V0 = π ( 2 ) =
4. a. 3
10. cm3
3 3
G ( 2.1) = ( 2.1) + 1 = 9.261 + 1 = 10.261
3 4 62.5π 125π
V1 = π ( 2.5 ) =
3
b. = cm3
3 3 6
G ( 2.1) − G ( 2 ) = 10.261 − 9 = 1.261 125π 32π
c. ΔV = V1 − V0 = cm3 − cm3
6 3
G ( 2.1) − G ( 2 ) 61
d. =
1.261
= 12.61 = π cm3 ≈ 31.940 cm3
2.1 − 2 0.1 6
11. a. North plane has traveled 600miles. East
G ( a + h) = ( a + h) + 1
3
e. plane has traveled 400 miles.
= a 3 + 3a 2 h + 3ah 2 + h3 + 1
d = 6002 + 4002
b.
G ( a + h ) − G ( a ) = ⎡( a + h ) + 1⎤ − ⎡ a + 1⎤
3 3
f. = 721 miles
⎣ ⎦ ⎣ ⎦
(
= a3 + 3a 2 h + 3ah 2 + h3 + 1 − a 3 + 1 ) ( ) d = 6752 + 5002
2 2 3
c.
= 3a h + 3ah + h = 840 miles
G ( a + h) − G ( a) 3a 2 h + 3ah 2 + h3
g. =
(a + h) − a h
= 3a 2 + 3ah + h 2
G ( a + h) − G ( a)
h. lim = lim 3a 2 + 3ah + h 2
h→0 (a + h) − a h →0
= 3a 2
5. a. ( a + b )3 = a3 + 3a 2b +
b. ( a + b ) 4 = a 4 + 4 a 3b +
c. ( a + b )5 = a 5 + 5 a 4 b +
6. ( a + b )n = a n + na n −1b +
7. sin ( x + h ) = sin x cos h + cos x sin h
8. cos ( x + h ) = cos x cos h − sin x sin h
9. a. The point will be at position (10, 0 ) in all
three cases ( t = 1, 2,3 ) because it will have
made 4, 8, and 12 revolutions respectively.
b. Since the point is rotating at a rate of 4
revolutions per second, it will complete 1
1
revolution after second. Therefore, the
4
point will first return to its starting position
1
at time t = .
4
Instructor’s Resource Manual Review and Preview 93
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form
or by any means, without permission in writing from the publisher.