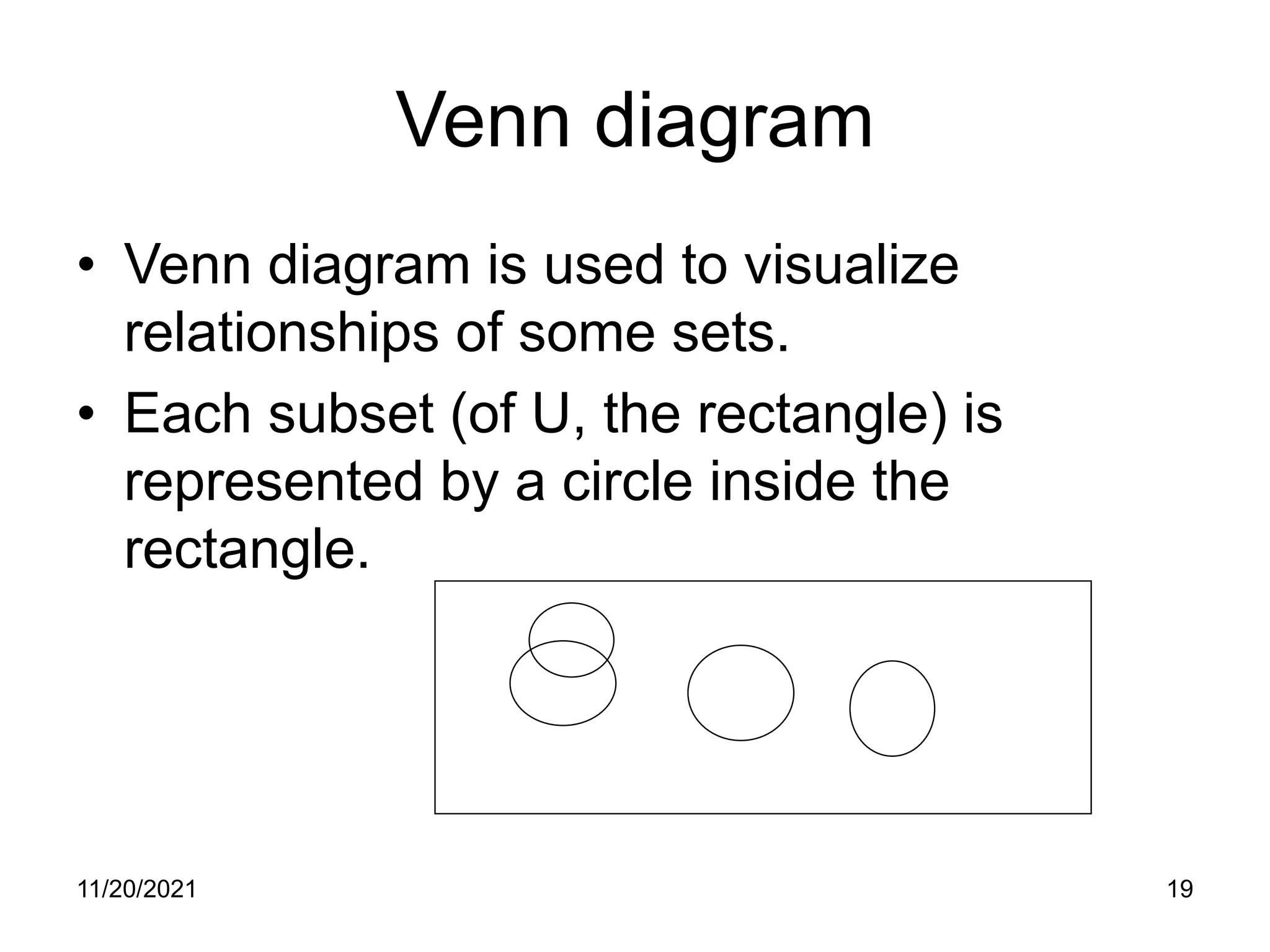
The document discusses basic concepts of set theory including defining sets, set operations like union and intersection, proofs of set identities using techniques like mutual inclusion, and applications of set theory concepts like the pigeonhole principle. It provides examples and explanations of fundamental set theory terms and concepts such as members, subsets, power sets, Venn diagrams, and proofs of set properties and identities.































![11/20/2021 33
Algebraic proof examples
• Prove:
[A ∪ (B ∩ C)] ∩ ([A’ ∪ (B ∩ C)] ∩ (B ∩ C)’) = ∅
Proof:
[A ∪ (B ∩ C)] ∩ ([A’ ∪ (B ∩ C)] ∩ (B ∩ C)’)
= ([A ∪ (B ∩ C)] ∩ [A’ ∪ (B ∩ C)]) ∩ (B∩C)’ (associative)
= ([(B ∩ C)∪ A] ∩ [(B ∩ C) ∪ A’]) ∩ (B∩C)’ (commutative)
= [(B ∩ C)∪ (A ∩ A’)] ∩ (B ∩ C)’ (distributive)
= [(B ∩ C)∪ ∅] ∩ (B ∩ C)’ (complement)
= (B ∩ C) ∩ (B ∩ C)’ (Identity)
= ∅ (identity)](https://image.slidesharecdn.com/discretestructurelecture78-220407192643/75/Discrete-Structure-Lecture-7-8-pdf-33-2048.jpg)








