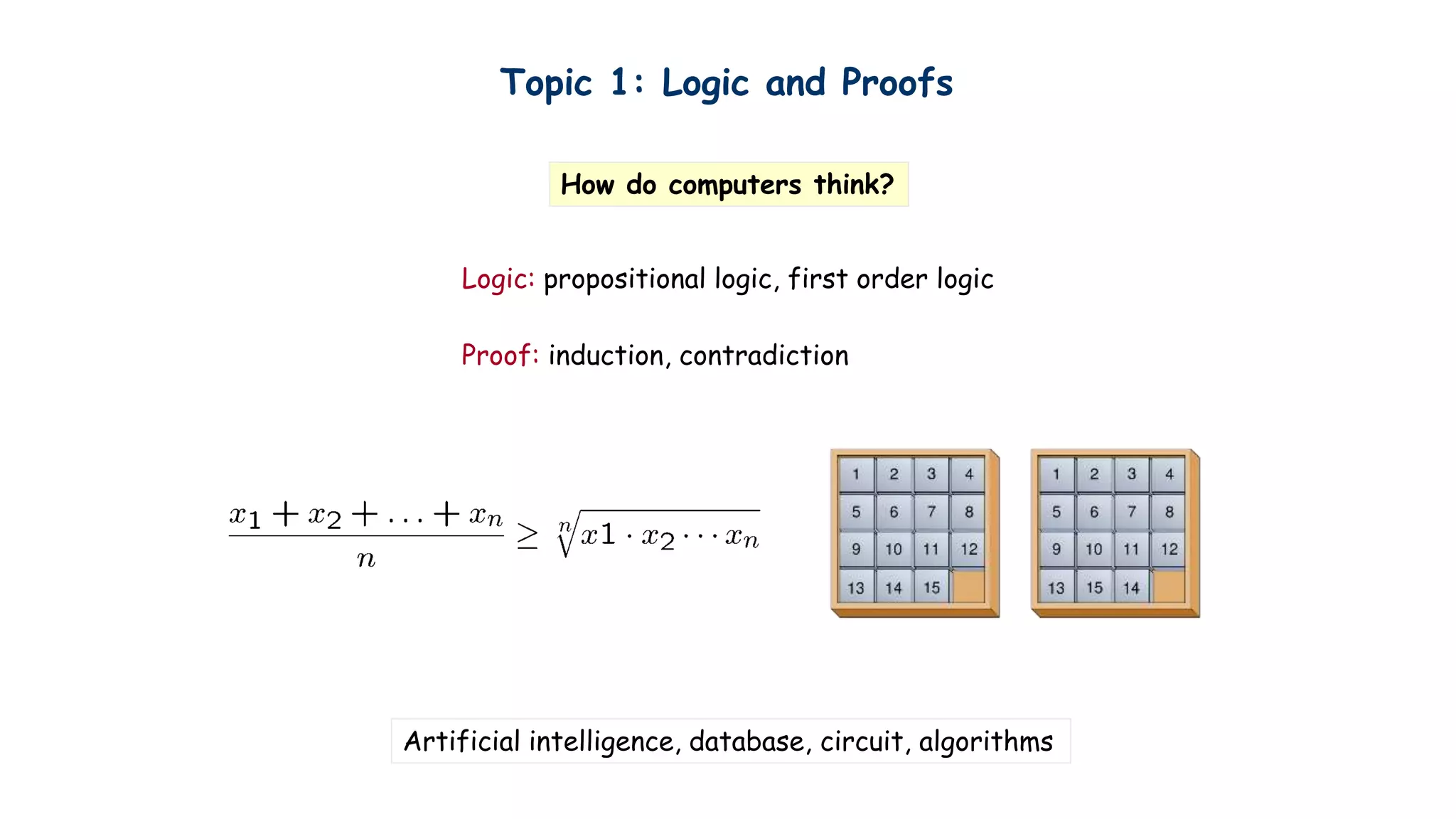
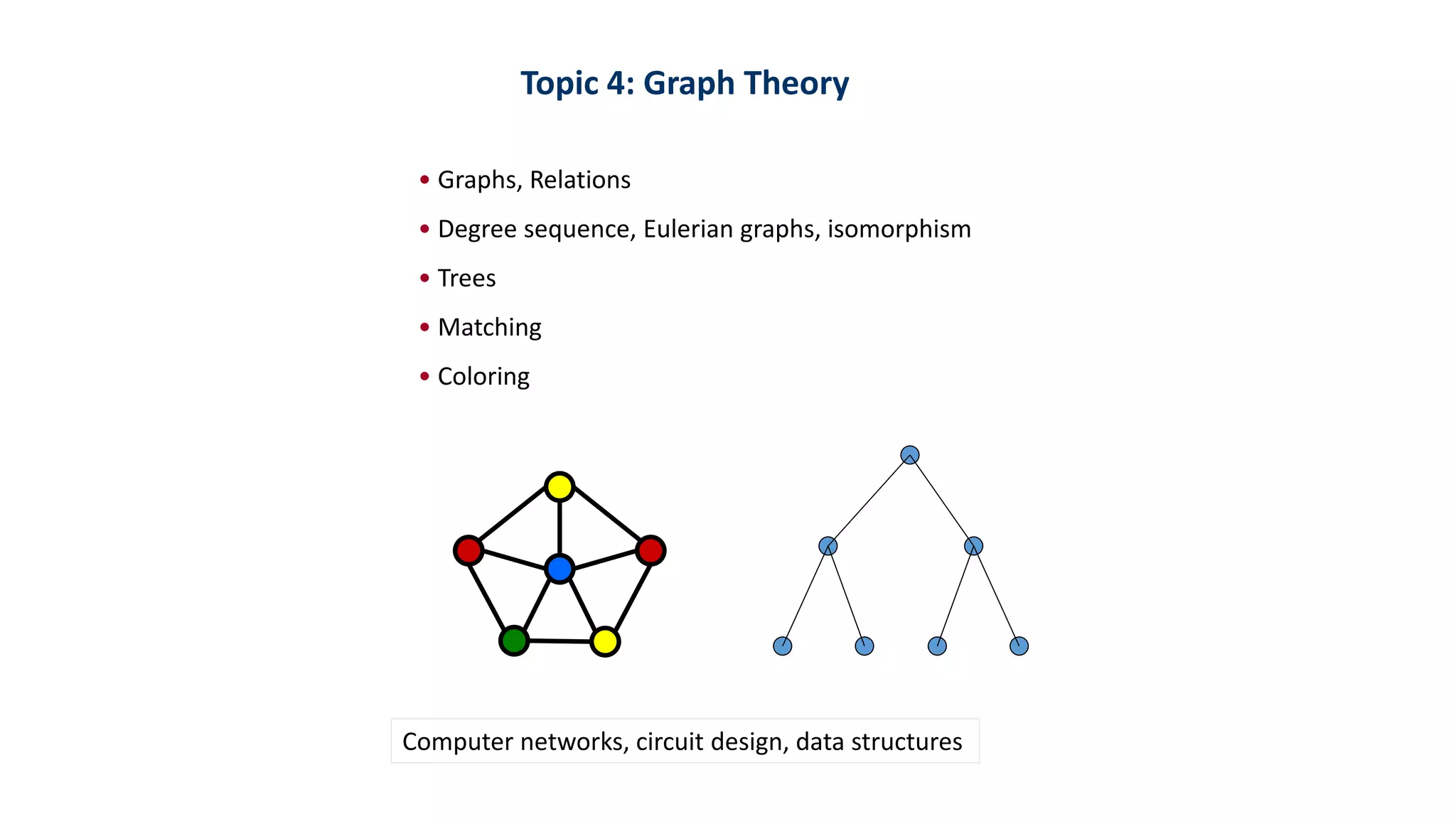
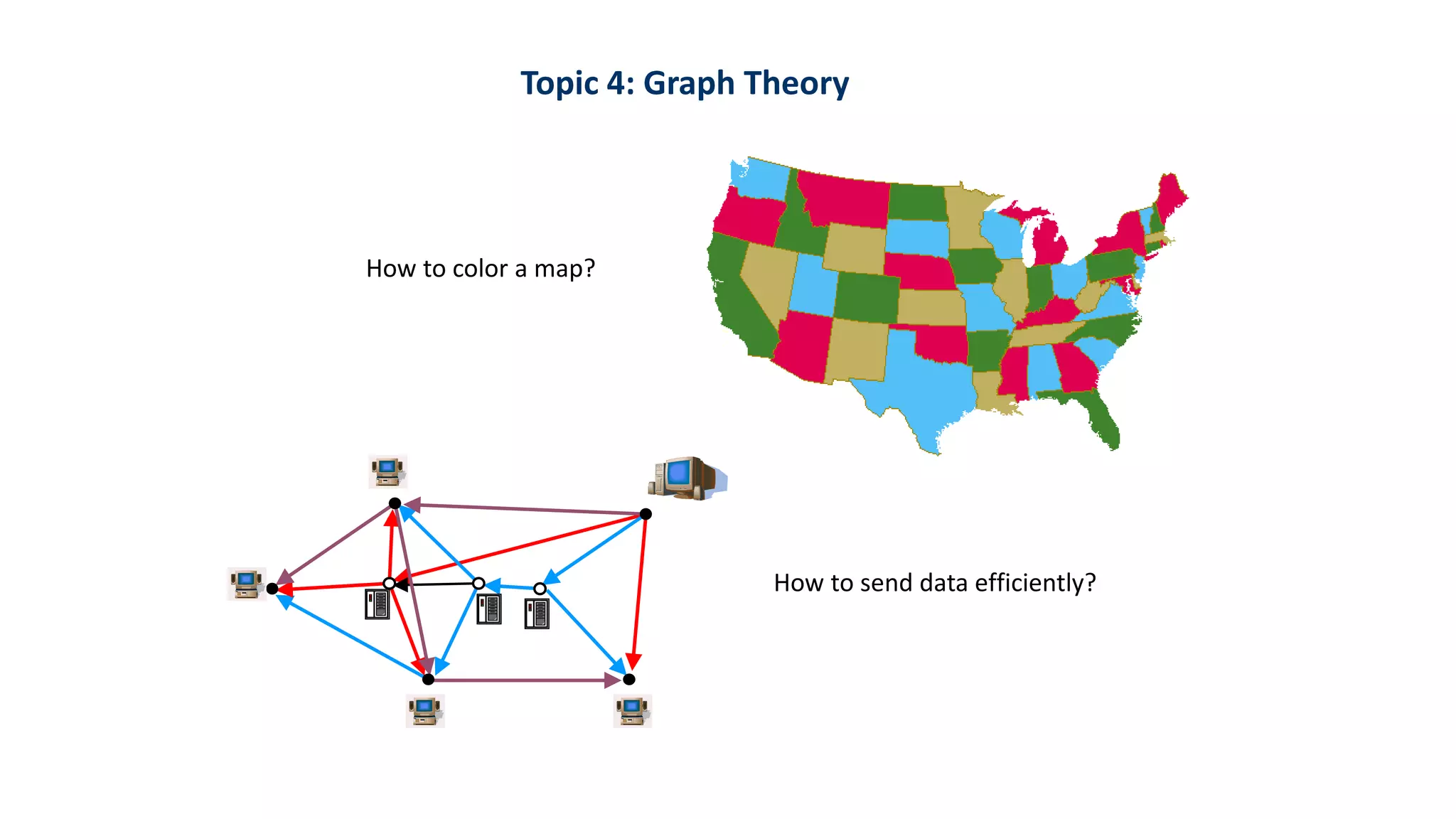
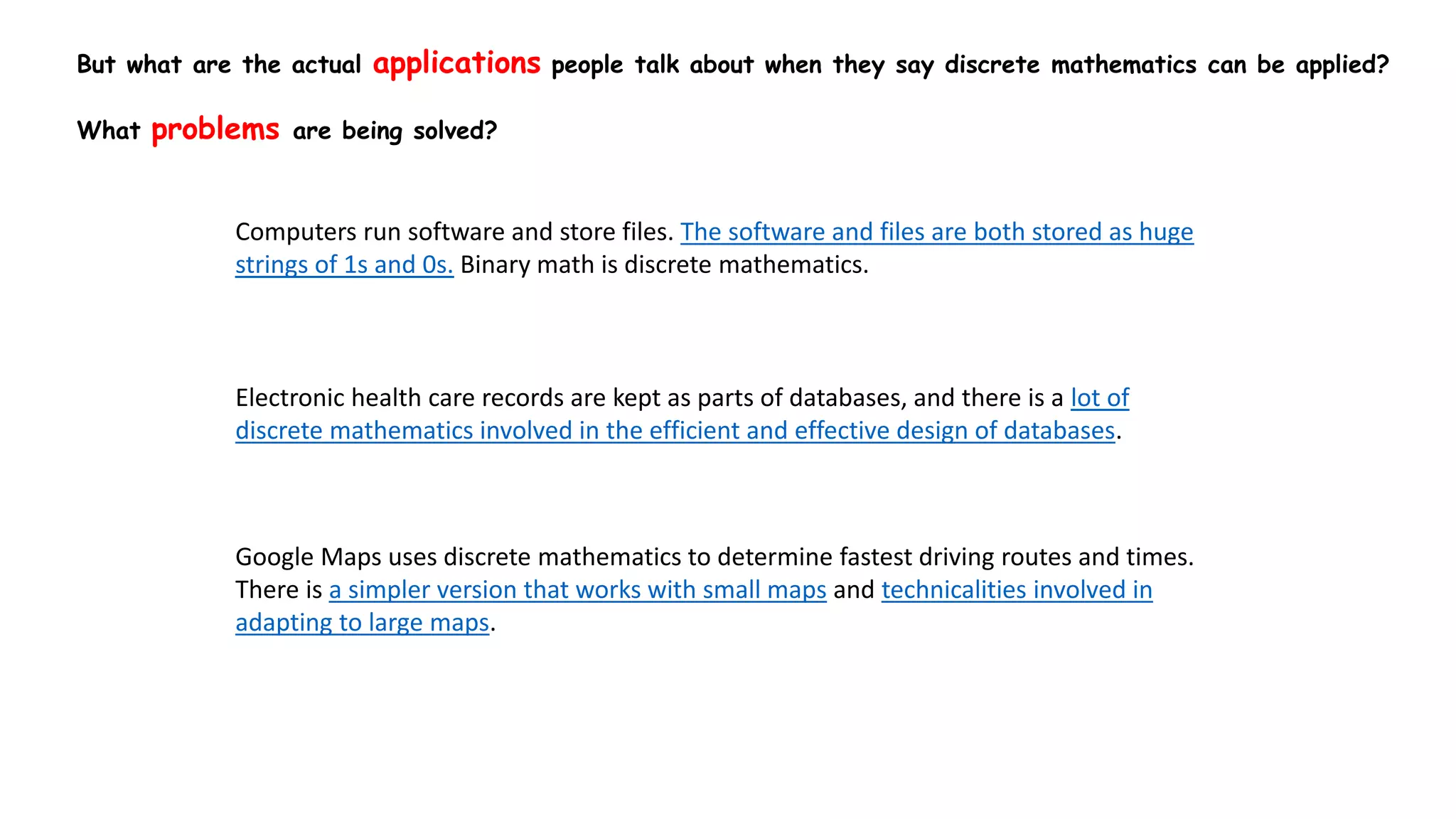
Discrete mathematics is the study of mathematical structures that are discrete rather than continuous. It has many applications in computer science, as computers use discrete structures to represent and manipulate data. Some key topics in discrete mathematics include logic and proofs, number theory, counting, and graph theory. These topics help with problem solving, algorithms, data structures, cryptography, and the design of efficient computer systems and networks. Examples of problems solved with discrete mathematics include the fastest sorting algorithms, map coloring, efficient data transmission, electronic health records, and Google Maps routing.

1. DISCRETE MATHEMATICAL STRUCTURES
17CS36
By
Sharmila Chidaravalli
Asst. Prof.
Dept. of ISE
Global Academy of Technology

2. Introduction
What is Discrete Mathematics?
Why Study DMS?
Applications of DMS

3. Discrete Mathematics
Number of students in your class
Particular value
Height of the students in the class
Continuous Value, vary from student to student
Digital : Discrete
Analog : Continuous
What?
Discrete math is not the name of the branch of mathematics like number theory,algebra,calculus
etc.Rather it’s a description of branches of math that all have the common feature that they
are “discrete” rather than “continuous”.

4. Why Study DMS???

5. Computers use discrete structures to represent and manipulate data.
Computer Science is not Programming
Computer Science is not Software Engineering
Edsger Dijkstra: “Computer Science is no more about computers than Astronomy is about telescopes.”
Computer Science is about problem solving.
Better Understanding of Digital Computers 1
0

6. Mathematics is at the heart of problem solving
Defining a problem requires mathematical rigor
Use and analysis of models, data structures, algorithms requires a solid foundation of mathematics
To justify why a particular way of solving a problem is correct or efficient (i.e., better than
another way) requires analysis with a well-defined mathematical model.
Generally :Logic Making and Problem –Solving Capabilities

7. Why Discrete Mathematics?
Design efficient computer systems.
• How did Google manage to build a fast search engine?
• What is the foundation of internet security?
algorithms, data structures, database,
parallel computing, distributed systems,
cryptography, computer networks…
Logic, number theory, counting, graph theory…

8. Topic 1: Logic and Proofs
Logic: propositional logic, first order logic
Proof: induction, contradiction
How do computers think?
Artificial intelligence, database, circuit, algorithms

9. Topic 2: Number Theory
• Number sequence
• (Extended) Euclidean algorithm
• Prime number, modular arithmetic, Chinese remainder theorem
• Cryptography, RSA protocol
Cryptography, coding theory, data structures

10. Topic 3: Counting
• Sets and Functions
• Combinations, Permutations, Binomial theorem
• Counting by mapping, pigeonhole principle
• Recursions
Probability, algorithms, data structures
A B
C

11. Topic 3: Counting
How many steps are needed to sort n numbers?
Algorithm 1 (Bubble Sort):
Every iteration moves the i-th smallest number to the i-th position
Algorithm 2 (Merge Sort):
Which algorithm runs faster?

12. Topic 4: Graph Theory
• Graphs, Relations
• Degree sequence, Eulerian graphs, isomorphism
• Trees
• Matching
• Coloring
Computer networks, circuit design, data structures

13. Topic 4: Graph Theory
How to color a map?
How to send data efficiently?

15. But what are the actual applications people talk about when they say discrete mathematics can be applied?
What problems are being solved?
Computers run software and store files. The software and files are both stored as huge
strings of 1s and 0s. Binary math is discrete mathematics.
Electronic health care records are kept as parts of databases, and there is a lot of
discrete mathematics involved in the efficient and effective design of databases.
Google Maps uses discrete mathematics to determine fastest driving routes and times.
There is a simpler version that works with small maps and technicalities involved in
adapting to large maps.

16. Encryption and decryption are part of cryptography, which is part of
discrete mathematics.
Wiring a computer network using the least amount of cable is
a minimum-weight spanning tree problem.
Designing password criteria is a counting problem: Is the space of passwords
chosen large enough that a hacker can't break into accounts just by trying all
the possibilities? How long do passwords need to be in order to resist such
attacks? (find out here!)
Area codes: How do we know when we need more area codes
to cover the phone numbers in a region? This is a basic
combinatorics problem.
http://www.mathily.org/dm-rw.html

17. Text Book
1. Ralph P. Grimaldi: Discrete and Combinatorial Mathematics, , 5th Edition, Pearson Education.
2004.
Reference Book
1. Basavaraj S Anami and Venakanna S Madalli: Discrete Mathematics – A Concept based approach,
Universities Press, 2016
2. Kenneth H. Rosen: Discrete Mathematics and its Applications, 6th Edition, McGraw Hill, 2007.
3. Jayant Ganguly: A Treatise on Discrete Mathematical Structures, Sanguine-Pearson, 2010.
4. D.S. Malik and M.K. Sen: Discrete Mathematical Structures: Theory and Applications, Thomson, 2004.
5. Thomas Koshy: Discrete Mathematics with Applications, Elsevier, 2005, Reprint 2008.