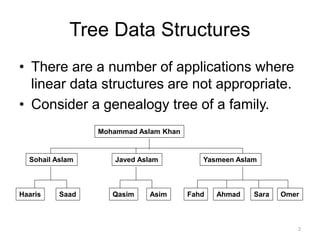
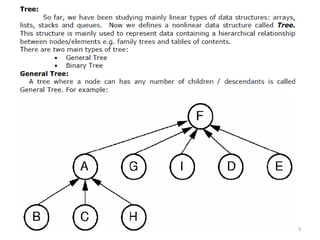
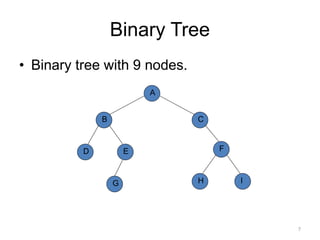
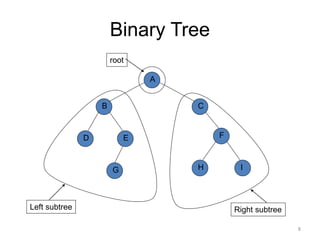
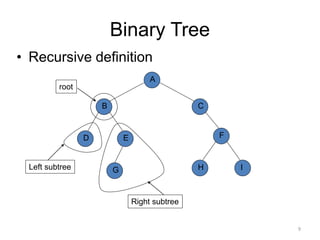
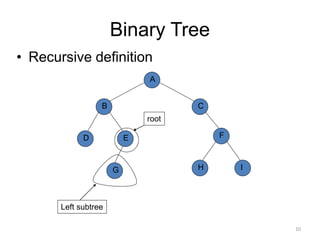
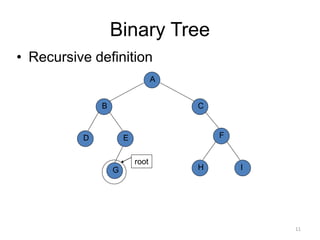
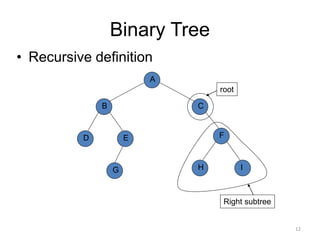
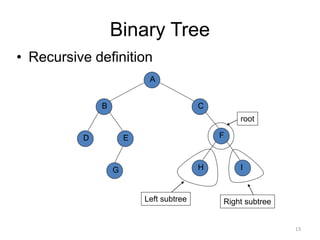
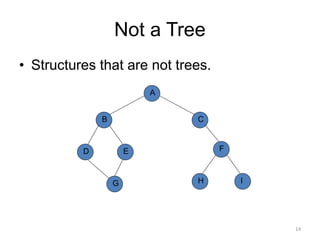
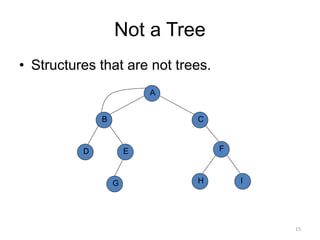
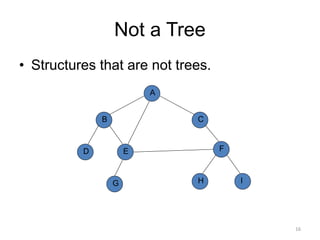
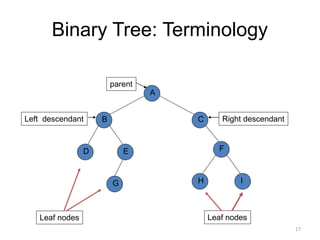
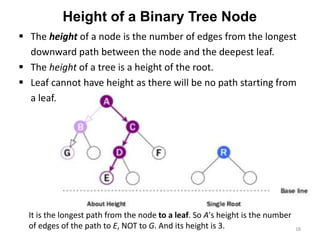
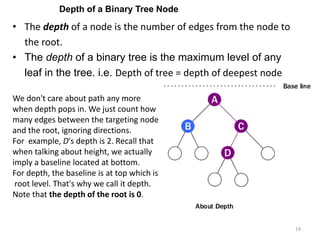
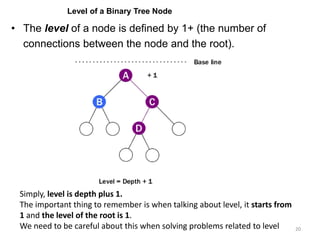
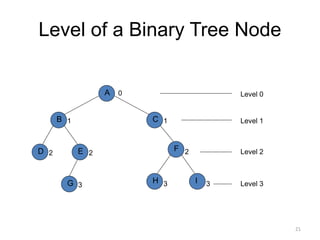
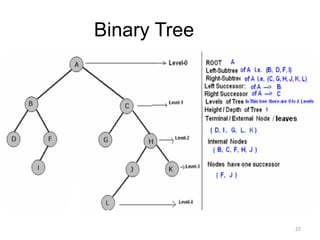
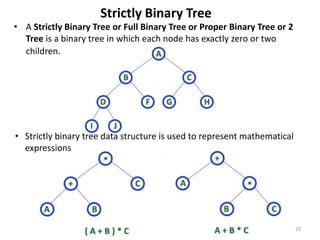
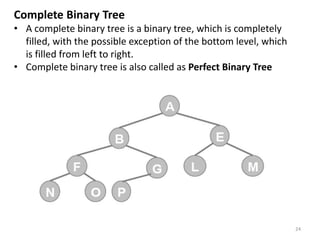
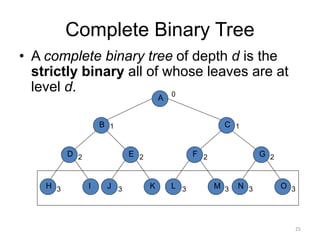
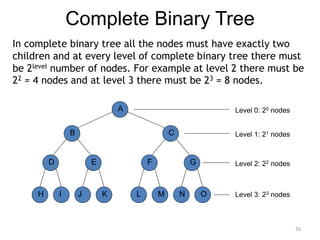
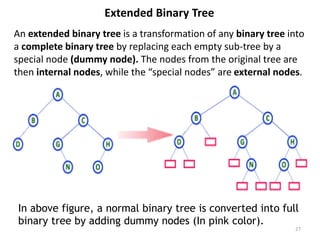
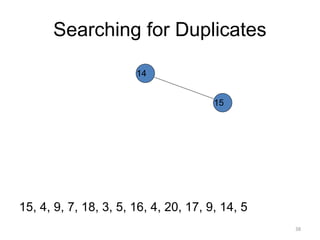
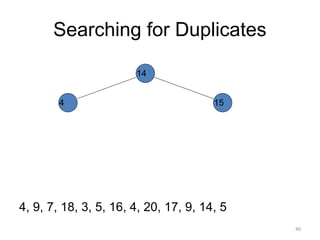
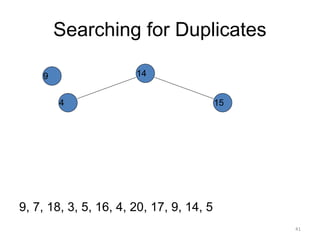
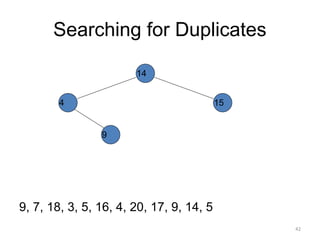
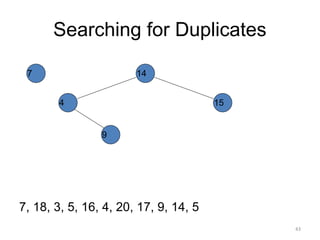
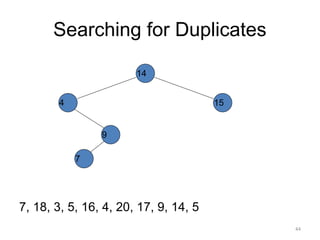
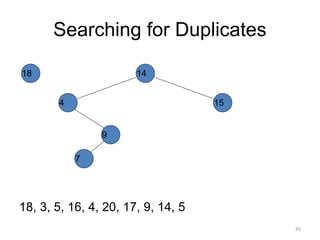
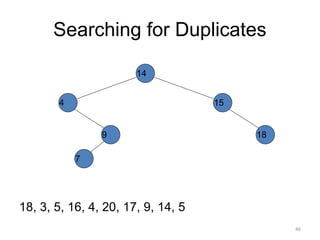
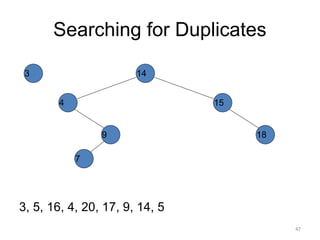
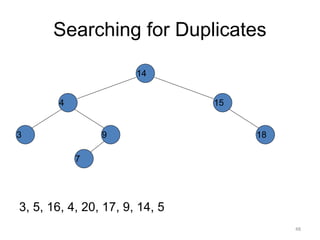
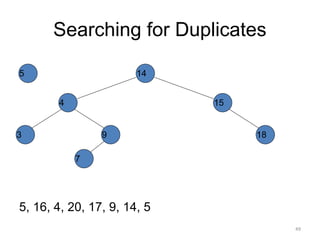
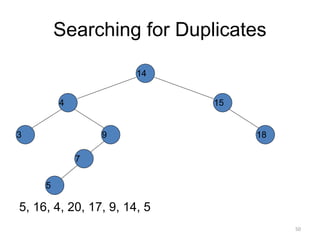
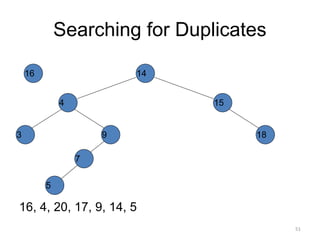
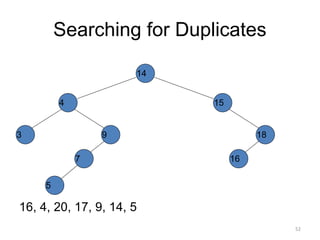
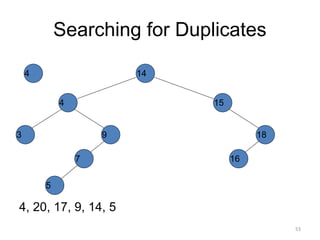
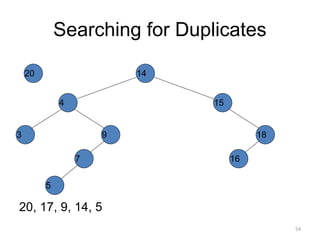
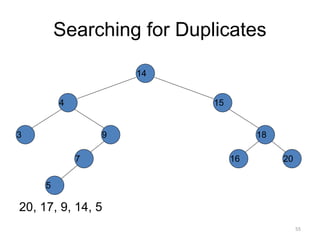
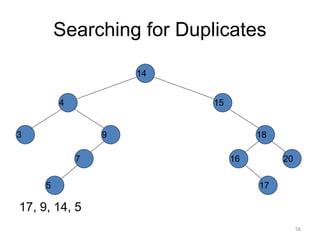
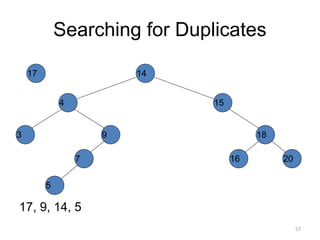
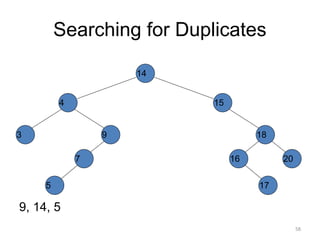
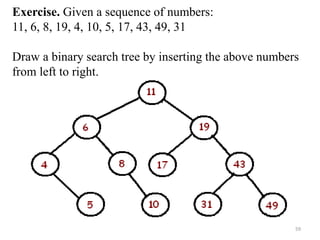
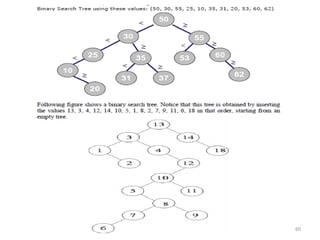
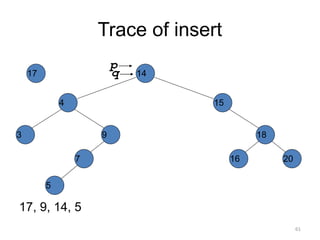
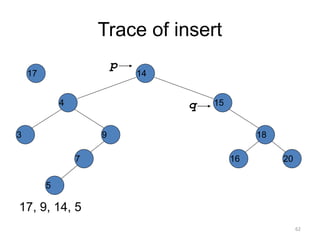
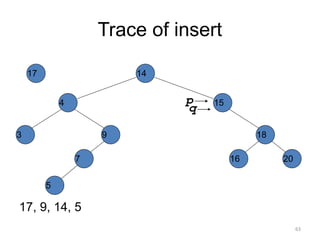
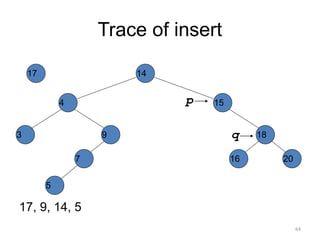
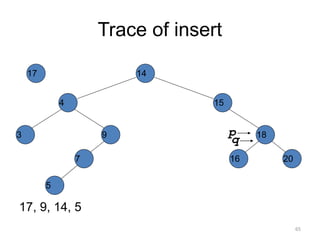
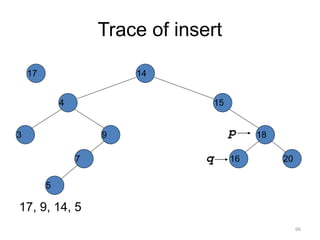
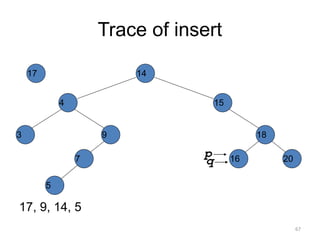
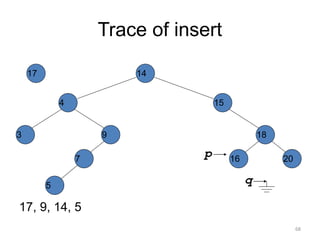
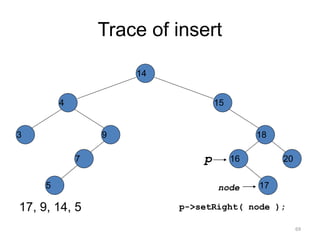
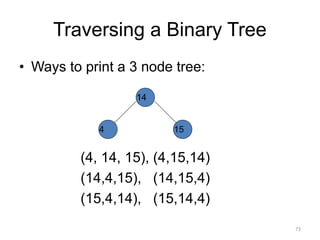
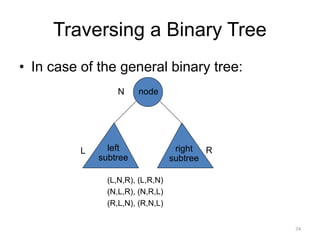
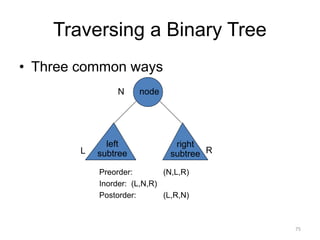
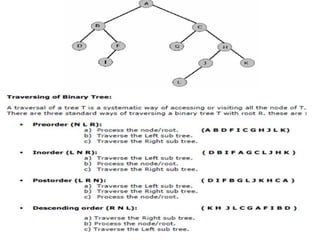
The document discusses binary trees and their traversal. It begins by defining binary trees as trees where each node has at most two children. It then discusses different binary tree terminology like left and right subtrees, root, internal and leaf nodes. Different types of binary trees are also covered like full/strict binary trees and complete binary trees. Various binary tree operations and applications are described like searching for duplicates in a list using a binary search tree. Tracing insertion of nodes in a binary search tree is also demonstrated through an example.

1. Data Structures & Algorithm
CSC-102
Lecture 5
Binary Trees Traversing
Lecturer: Syeda Nazia Ashraf
1

2. Tree Data Structures
• There are a number of applications where
linear data structures are not appropriate.
• Consider a genealogy tree of a family.
Mohammad Aslam Khan
Sohail Aslam Javed Aslam Yasmeen Aslam
Saad
Haaris Qasim Asim Fahd Ahmad Sara Omer
2

3. 3

4. Tree Data Structure
• A linear linked list will not be able to
capture the tree-like relationship with
ease.
• Shortly, we will see that for applications
that require searching, linear data
structures are not suitable.
• We will focus our attention on binary trees.
4

5. Binary Tree
• A tree in which every node can have a maximum of
two children is called as Binary Tree.
• In a binary tree, every node can have either 0
children or 1 child or 2 children but not more than 2
children. A
B
D
H
C
E F
G I
J
K
5

6. Binary Tree
• A binary tree is a finite set of elements
that is either empty or is partitioned into
three disjoint subsets.
• The first subset contains a single element
called the root of the tree.
• The other two subsets are themselves
binary trees called the left and right
subtrees.
• Each element of a binary tree is called a
node of the tree.
6

7. Binary Tree
• Binary tree with 9 nodes.
A
B
D
H
C
E F
G I
7

8. Binary Tree
A
B
D
H
C
E F
G I
Left subtree
root
Right subtree
8

9. Binary Tree
• Recursive definition
A
B
D
H
C
E F
G I
Left subtree
root
Right subtree
9

10. Binary Tree
• Recursive definition
A
B
D
H
C
E F
G I
Left subtree
root
10

11. Binary Tree
• Recursive definition
A
B
D
H
C
E F
G I
root
11

12. Binary Tree
• Recursive definition
A
B
D
H
C
E F
G I
root
Right subtree
12

13. Binary Tree
• Recursive definition
A
B
D
H
C
E F
G I
root
Right subtree
Left subtree
13

14. Not a Tree
• Structures that are not trees.
A
B
D
H
C
E F
G I
14

15. Not a Tree
• Structures that are not trees.
A
B
D
H
C
E F
G I
15

16. Not a Tree
• Structures that are not trees.
A
B
D
H
C
E F
G I
16

17. Binary Tree: Terminology
A
B
D
H
C
E F
G I
parent
Left descendant Right descendant
Leaf nodes Leaf nodes
17

18. Height of a Binary Tree Node
▪ The height of a node is the number of edges from the longest
downward path between the node and the deepest leaf.
▪ The height of a tree is a height of the root.
▪ Leaf cannot have height as there will be no path starting from
a leaf.
18
It is the longest path from the node to a leaf. So A's height is the number
of edges of the path to E, NOT to G. And its height is 3.

19. 19
• The depth of a node is the number of edges from the node to
the root.
• The depth of a binary tree is the maximum level of any
leaf in the tree. i.e. Depth of tree = depth of deepest node
We don't care about path any more
when depth pops in. We just count how
many edges between the targeting node
and the root, ignoring directions.
For example, D's depth is 2. Recall that
when talking about height, we actually
imply a baseline located at bottom.
For depth, the baseline is at top which is
root level. That's why we call it depth.
Note that the depth of the root is 0.
Depth of a Binary Tree Node

20. 20
• The level of a node is defined by 1+ (the number of
connections between the node and the root).
Level of a Binary Tree Node
Simply, level is depth plus 1.
The important thing to remember is when talking about level, it starts from
1 and the level of the root is 1.
We need to be careful about this when solving problems related to level

21. Level of a Binary Tree Node
A
B
D
H
C
E F
G I
1
0
1
2 2 2
3 3 3
Level 0
Level 1
Level 2
Level 3
21

22. Binary Tree
22

23. 23
• A Strictly Binary Tree or Full Binary Tree or Proper Binary Tree or 2
Tree is a binary tree in which each node has exactly zero or two
children.
Strictly Binary Tree
• Strictly binary tree data structure is used to represent mathematical
expressions

24. 24
Complete Binary Tree
• A complete binary tree is a binary tree, which is completely
filled, with the possible exception of the bottom level, which
is filled from left to right.
• Complete binary tree is also called as Perfect Binary Tree

25. Complete Binary Tree
• A complete binary tree of depth d is the
strictly binary all of whose leaves are at
level d.
A
B
N
C
G
O
1
0
1
2
3 3
L
F
M
2
3 3
H
D
I
2
3 J
E
K
2
3
25

26. Complete Binary Tree
A
B
Level 0: 20 nodes
H
D
I
E
J K
C
L
F
M
G
N O
Level 1: 21 nodes
Level 2: 22 nodes
Level 3: 23 nodes
26
In complete binary tree all the nodes must have exactly two
children and at every level of complete binary tree there must
be 2level number of nodes. For example at level 2 there must be
22 = 4 nodes and at level 3 there must be 23 = 8 nodes.

27. 27
An extended binary tree is a transformation of any binary tree into
a complete binary tree by replacing each empty sub-tree by a
special node (dummy node). The nodes from the original tree are
then internal nodes, while the “special nodes” are external nodes.
In above figure, a normal binary tree is converted into full
binary tree by adding dummy nodes (In pink color).
Extended Binary Tree

28. Operations on Binary Tree
• There are a number of operations that can
be defined for a binary tree.
• If p is pointing to a node in an existing tree
then
▪ left(p) returns pointer to the left subtree
▪ right(p) returns pointer to right subtree
▪ parent(p) returns the father of p
▪ brother(p) returns brother of p.
▪ info(p) returns content of the node.
28

29. Operations on Binary Tree
• In order to construct a binary tree, the
following can be useful:
• setLeft(p,x) creates the left child node of p.
The child node contains the info ‘x’.
• setRight(p,x) creates the right child node
of p. The child node contains the info ‘x’.
29

30. Binary Search Tree
• A binary tree with the property: that items
in the left subtree are smaller than the root
and items are larger or equal in the right
subtree is called a binary search tree
(BST).
• The tree we built for searching for
duplicate numbers was a binary search
tree.
• BST and its variations play an important
role in searching algorithms.
30

31. Applications of Binary Trees
• A binary tree is a useful data structure
when two-way decisions must be made at
each point in a process.
• For example, suppose we wanted to find
all duplicates in a list of numbers:
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
31

32. Applications of Binary Trees
• One way of finding duplicates is to
compare each number with all those that
precede it.
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
32

33. Searching for Duplicates
• If the list of numbers is large and is
growing, this procedure involves a large
number of comparisons.
• A linked list could handle the growth but
the comparisons would still be large.
• The number of comparisons can be
drastically reduced by using a binary tree.
• The tree grows dynamically like the linked
list.
33

34. Searching for Duplicates
• The binary tree is built in a special way.
• The first number in the list is placed in a
node that is designated as the root of a
binary tree.
• Initially, both left and right subtrees of the
root are empty.
• We take the next number and compare it
with the number placed in the root.
• If it is the same then we have a duplicate.
34

35. Searching for Duplicates
• Otherwise, we create a new tree node and
put the new number in it.
• The new node is made the left child of the
root node if the second number is less
than the one in the root.
• The new node is made the right child if the
number is greater than the one in the root.
35

36. Searching for Duplicates
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
36

37. Searching for Duplicates
15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
37

38. Searching for Duplicates
15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
38

39. Searching for Duplicates
4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
39

40. Searching for Duplicates
4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
40

41. Searching for Duplicates
9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
41

42. Searching for Duplicates
9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
42

43. Searching for Duplicates
7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
43

44. Searching for Duplicates
7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
44

45. Searching for Duplicates
18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
45

46. Searching for Duplicates
18, 3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
46

47. Searching for Duplicates
3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
47

48. Searching for Duplicates
3, 5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
48

49. Searching for Duplicates
5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
49

50. Searching for Duplicates
5, 16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
50

51. Searching for Duplicates
16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
16
51

52. Searching for Duplicates
16, 4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
16
52

53. Searching for Duplicates
4, 20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
16
4
53

54. Searching for Duplicates
20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
16
20
54

55. Searching for Duplicates
20, 17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
55

56. Searching for Duplicates
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
56

57. Searching for Duplicates
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
57

58. Searching for Duplicates
9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
58

59. 59
Exercise. Given a sequence of numbers:
11, 6, 8, 19, 4, 10, 5, 17, 43, 49, 31
Draw a binary search tree by inserting the above numbers
from left to right.

60. 60

61. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
61

62. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
62

63. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
63

64. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
64

65. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
65

66. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
66

67. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
67

68. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
q
68

69. Trace of insert
17, 9, 14, 5
14
15
4
9
7
18
3
5
16 20
17
p
p->setRight( node );
node
69

70. Cost of Search
• If the binary tree is built out of n numbers,
how many comparisons are needed to find
out if a number x is in the tree?
• The depth of the complete binary tree built
using ‘n’ nodes will be log2(n+1) – 1.
• For example, for n=100,000, log2(100001)
is less than 20; the tree would be 20 levels
deep.
70

71. Cost of Search
• If the tree is complete binary or nearly
complete, searching through 100,000
numbers will require a maximum of 20
comparisons.
• Or in general, approximately log2(n).
• Compare this with a linked list of 100,000
numbers. The comparisons required could
be a maximum of n.
71

72. Traversing a Binary Tree
• Suppose we have a binary tree, ordered
(BST) or unordered.
• We want to print all the values stored in
the nodes of the tree.
• In what order should we print them?
72

73. Traversing a Binary Tree
• Ways to print a 3 node tree:
14
15
4
(4, 14, 15), (4,15,14)
(14,4,15), (14,15,4)
(15,4,14), (15,14,4)
73

74. Traversing a Binary Tree
• In case of the general binary tree:
node
(L,N,R), (L,R,N)
(N,L,R), (N,R,L)
(R,L,N), (R,N,L)
left
subtree
right
subtree
L
N
R
74

75. Traversing a Binary Tree
• Three common ways
node
Preorder: (N,L,R)
Inorder: (L,N,R)
Postorder: (L,R,N)
left
subtree
right
subtree
L
N
R
75

76. 76