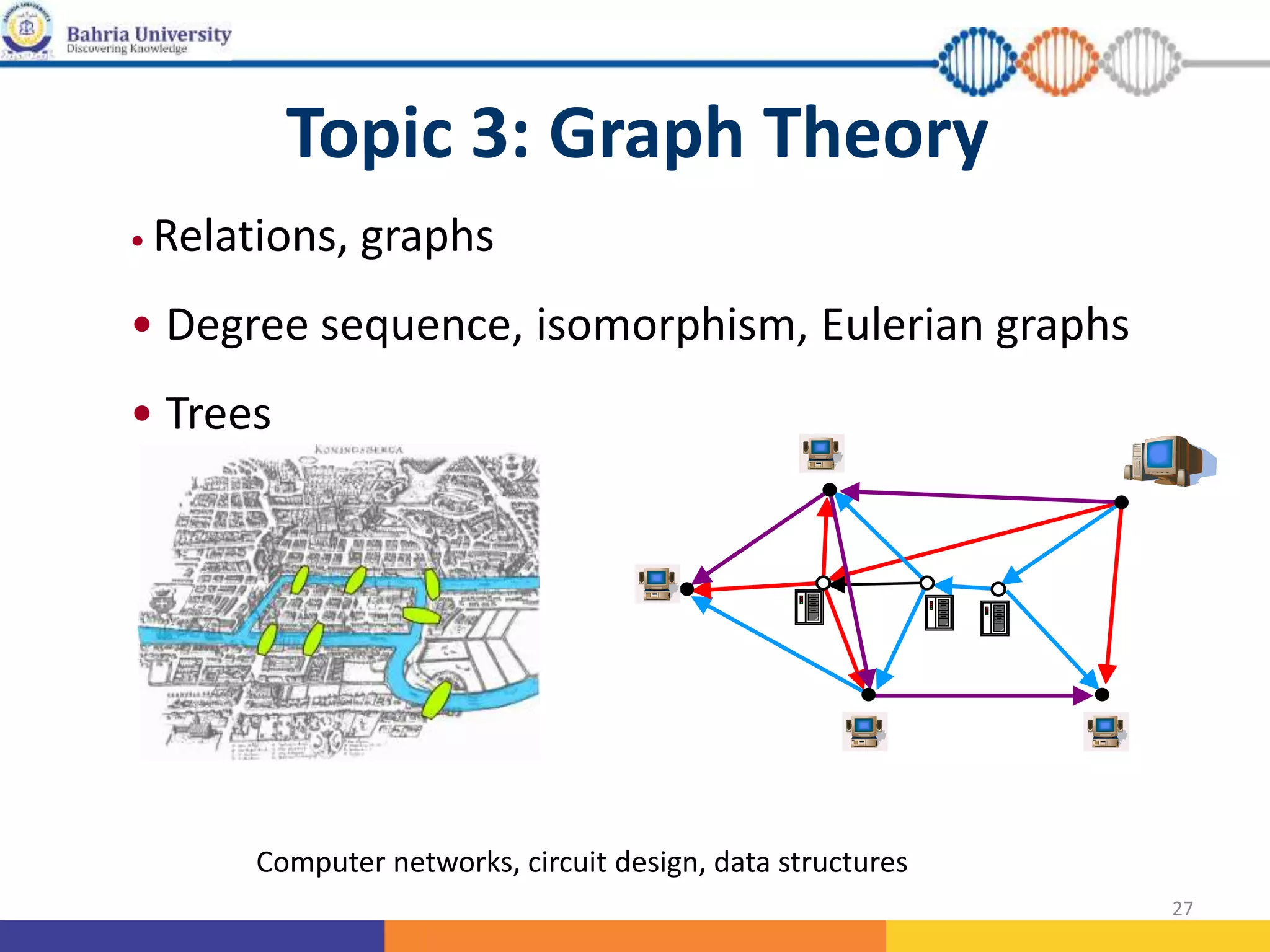
This document provides information about a Discrete Mathematics course. It outlines the course objectives, which are to provide students with basic discrete mathematics knowledge and skills in mathematical reasoning, problem solving, and understanding abstract structures. The course learning outcomes include understanding logic, proofs, sets, counting principles, relations, functions, graphs, and trees. The course code, title, credit hours, books, and assessment breakdown are also noted. The document concludes with an introduction to the topics that will be covered, including logic and proofs, counting, graph theory, and number theory.

1. 1

2. Todays Topics
Course Objectives
Outcomes
Reference Books
Marks distribution
Overview of main Topics
Introduction
2

3. Course Objectives
The main objective of this course is to provide
students with the basic knowledge of discrete
mathematics.
Other objectives are as follows:
• understand mathematical reasoning, logically
and mathematically
• improve problem-solving skills of enumerating
objects using combinatorial analysis
• know the abstract mathematical structures
used to represent discrete objects and
relationships between these objects
3

4. Course Learning Outcomes
Upon completion of the course, Students will be able to:
• Write an argument using logical notation and determine if the
argument is or is not valid.
• Demonstrate the ability to write and evaluate a proof or outline
the basic structure of and give examples of each proof
technique described.
• Understand the basic principles of sets and operations in sets.
• Prove basic set equalities.
• Apply counting principles to determine probabilities.
• Demonstrate an understanding of relations and functions and
be able to determine their properties.
• Demonstrate different traversal methods for trees and graphs.
• Model problems in Computer Science using graphs and trees.
4

5. Course Code: GSC-221
Course Title: Discrete Mathematics
Credit Hours: 3
Abbreviation: DM
Prerequisite: -
Type of Course: Core
Course Description:
Propositional statements, predicate logic and its truth values,
quantifiers, methods of proofs, composition, Sequences, types of
sequences, Elementary number theory, mathematical Induction,
Recursive definition, recursively defined sets and structures, Basic
counting rules, pigeon hole principle, permutation, combination,
Relations, reflexive, symmetry, transitive, equivalence relations,
Graphs, terminologies, graph models, types of graphs, representation
About Theory Course
5

6. Final
50%
Midterm
20%
Asgns
20%
Quizzes
10%
Scoring
Quizzes 10%
Assignments (Theoretical) 20%
Midterm Examination 20%
Final Examination 50%
Total 100%
Course Assessment
6

7. Books
• “DISCRETE MATHEMATICS AND ITS
APPLICATIONS” BY Kenneth H
Rosen. 7TH ED
• “DISCRETE MATHEMATICS WITH
APPLICATION” by Susanna S Epp.
4th ED
• “DISCRETE MATHEMATICS” by
Richard Johnson Baugh. 7th ED
7

8. Reference Books
• “DISCRETE MATHEMATICAL STRUCTURES” by
Kolman, busby & Ross. 4th ED
• “DISCRETE AND COMBINATORIAL
MATHEMATICS: AN APPLIED
INTRODUCTION” by Ralph P. Grimaldi.
• “LOGIC AND DISCRETE MATHEMATICS: A
COMPUTER SCIENCE PERSPECTIVE ” by
Winifred Grassman
8

9. Copying someone else’s work (partial or
complete) and submitting it as if it were one’s
own
Zero tolerance forplagiarism
Plagiarism

10. What we learn Next !!
Why DM?
What is DM?
History
Uses DM
Applications
10

11. Introduction to Discrete
Mathematics
11
Chapter 1: “The foundations: Logic and Proof”
Book: DISCRETE MATHEMATICS AND ITS
APPLICATIONS” BY Kenneth H Rosen. 7TH ED

12. Mathematics
12

13. Discrete Mathematics
13

14. • Discrete mathematics deals with objects
that come in discrete bundles, such as
integers, graphs and statements in logics
• e.g.,1 or 2 books
• Topics include probability, set theory
etc.
• Continuous mathematics deals with objects that vary
continuously,such as real numbers-vary smoothly
• e.g.,3.42 inches from a wall.
• Topic include calculus
• Think of digital watches versus analog watches
(ones where the second hand loops around
continuously withoutstopping)
Discrete Mathematics

15. Founder
Montes Archimedes is known
as the Father of Mathematics.
Mathematics is one of the
ancient sciences developed in
time immemorial
15
Paul Erdos is known as the father
of discrete mathematics.
In 1980s Discrete Mathematics
was introduce as a computer
science support course.

16. Why Discrete Mathematics?
16

17. Uses of discrete mathematics in computer
science
17

18. Cryptography The field of cryptography, which is the study of
how to create security structures and passwords for computers
and other electronic systems, is based entirely on discrete
mathematics.
 This is partly because computers send information in discrete --
or separate and distinct -- bits. Number theory, one important
part of discrete math, allows cryptographers to create and break
numerical passwords. Because of the quantity of money and the
amount of confidential information involved, cryptographers must
first have a solid background in number theory to show they can
provide secure passwords and encryption methods.
Why Study Discrete
Mathematics/Structures

19. Relational Databases Relational databases play a part in almost
every organization that must keep track of employees, clients or
resources.
A relational database connects the traits of a certain piece of
information.
For example, in a database containing client information, the
relational aspect of this database allows the computer system to
know how to link the client’s name, address, phone number and
other pertinent information. This is all done through the discrete
math concept of sets.
Sets allow information to be grouped and put in order. Since each
piece of information and each trait belonging to that piece of
information is discrete, the organization of such information in a
database requires discrete mathematical methods.
Why Study Discrete
Mathematics/Structures

20. Computer Algorithms: Algorithms are the rules by which a
computer operates.
• These rules are created through the laws of discrete
mathematics.
• A computer programmer uses discrete math to design efficient
algorithms.
• This design includes applying discrete math to determine the
number of steps an algorithm needs to complete, which implies
the speed of the algorithm. Because of discrete mathematical
applications in algorithms, today’s computers run faster than
ever before.
Why Study Discrete
Mathematics/Structures

21. Image Processing Image processing is a method to convert an
image into digital form and perform some operations on it
• In order to get an enhanced image or to extract some useful
information from it. It convert image as two dimensional
signals
Graph Theory Google Maps uses discrete mathematics to
determine fastest driving routes and times.
• There is a simpler version that works with small maps and
technicalities involved in adapting to large maps.
• Used in Data Mining and Networking as well.
Why Study Discrete
Mathematics/Structures

22. Why Discrete Mathematics?
• How many ways are there to choose a valid password on a computer
system?
• What is the probability of winning a lottery?
• Is there a link between two computers in a network?
• How can I identify spam e-mail messages?
• How can I encrypt a message so that no unintended recipient can read it?
• What is the shortest path between two cities using a transportation
system?
• How can a list of integers be sorted so that the integers are in increasing
order?
• How many steps are required to do such a sorting?
• How can it be proved that a sorting algorithm correctly sorts a list?
• How can a circuit that adds two integers be designed?
• How many valid Internet addresses are there? 22

23. Applications
Design efficient computer systems.
•How did Google manage to build a fast search engine?
•What is the foundation of internet security?
algorithms, data structures, database,
parallel computing, distributed systems,
cryptography, computer networks…
Logic, sets/functions, counting, graph theory…
23

24. Topic 1: Logic and Proofs
Logic: propositional logic, first order logic
Proof: induction, contradiction
How do computers think?
Artificial intelligence, database, circuit, algorithms
24

25. Topic 2: Counting
• Sets
• Combinations, Permutations, Binomial theorem
• Functions
• Counting by mapping, pigeonhole principle
• Recursions, generating functions
Probability, algorithms, data structures
25

26. Topic 2: Counting
How many steps are needed to sort n numbers?
26

27. Topic 3: Graph Theory
• Relations, graphs
• Degree sequence, isomorphism, Eulerian graphs
• Trees
Computer networks, circuit design, data structures
27

28. Topic 4: Number Theory
• Number sequence
• Euclidean algorithm
• Prime number
• Modular arithmetic
Cryptography, coding theory, data structures
28

29. 29