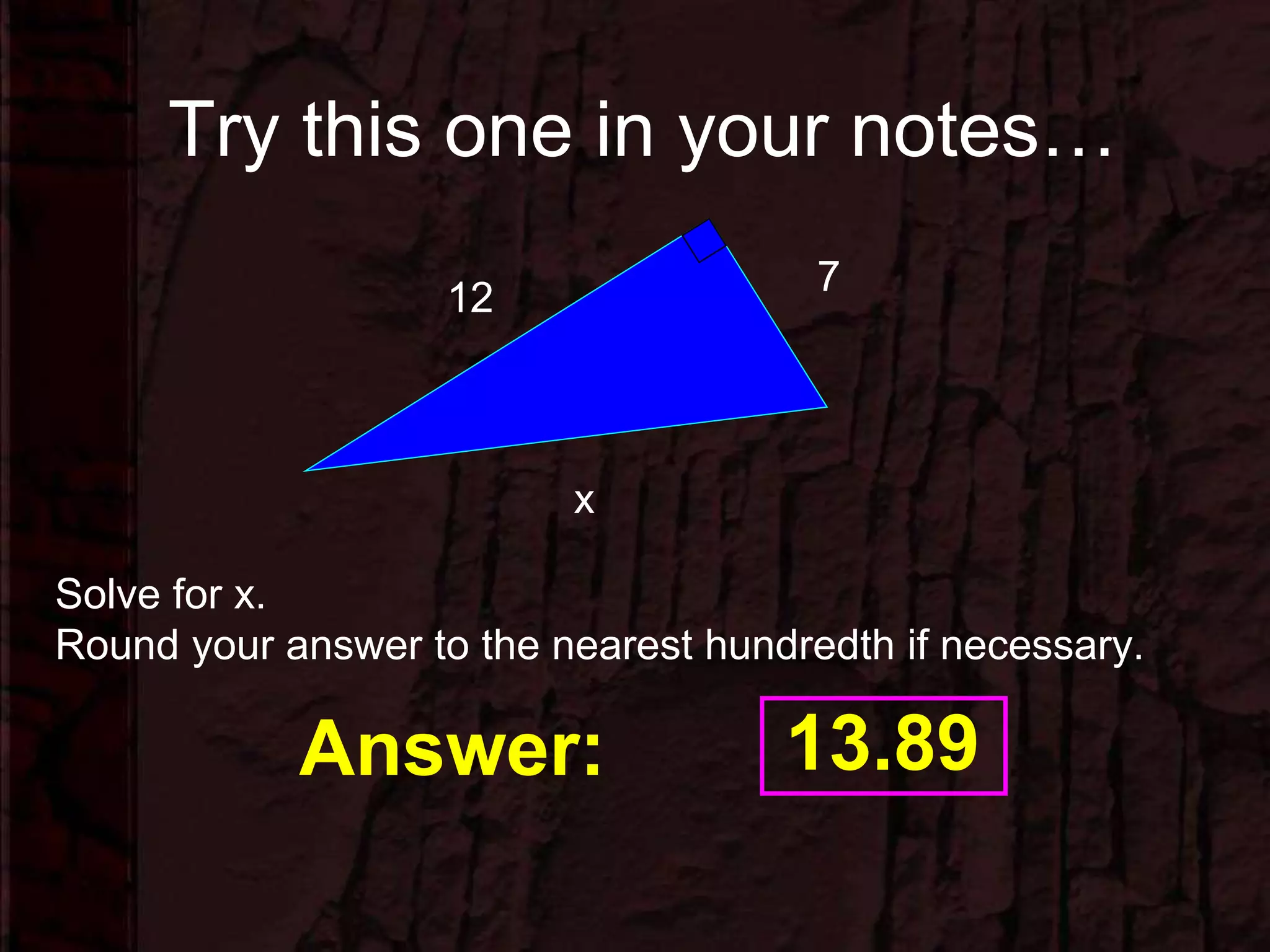
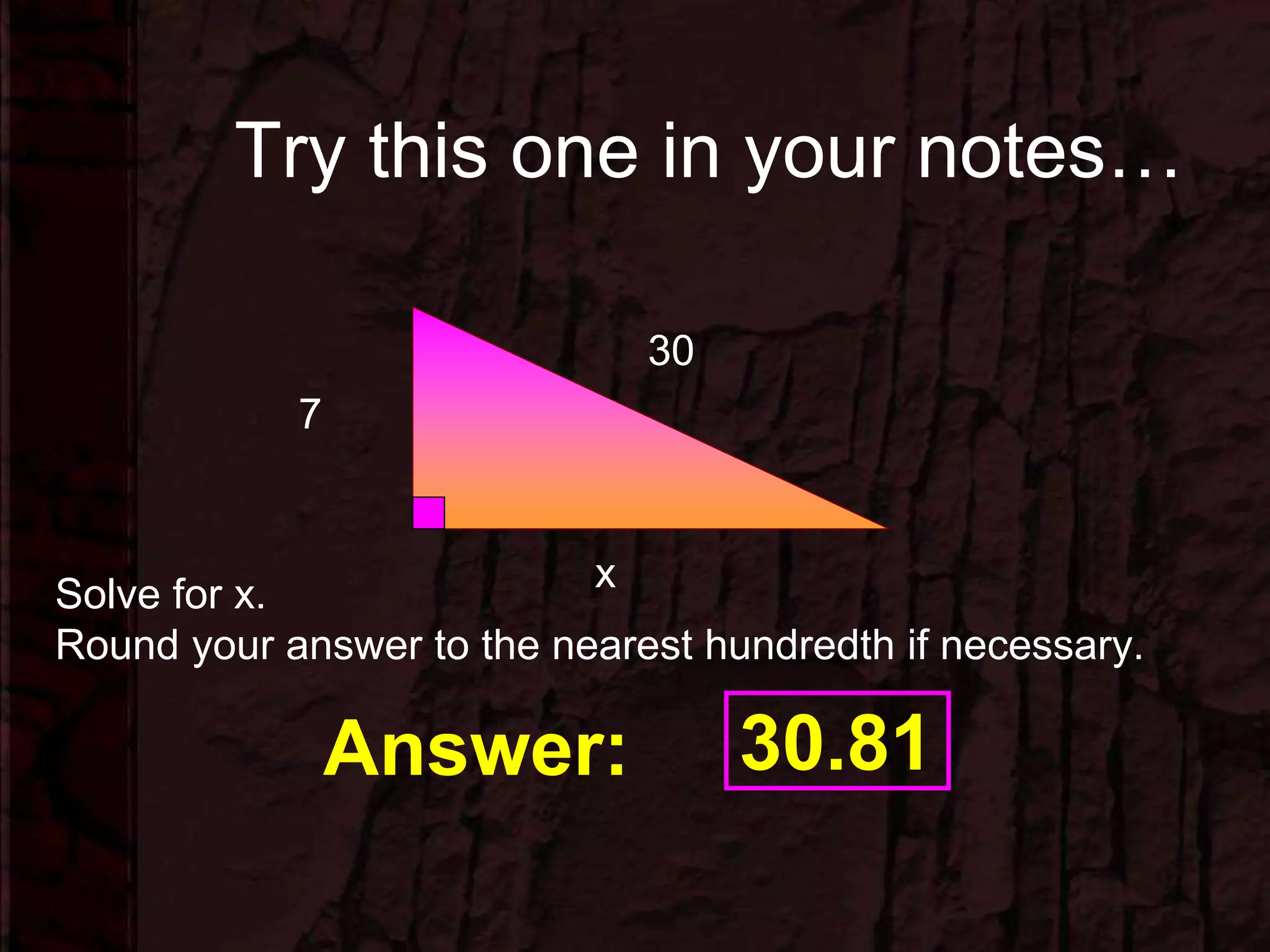
This document provides instruction on using the Pythagorean theorem to solve for missing sides of right triangles. It defines the Pythagorean theorem as a2 + b2 = c2, where c is the hypotenuse. It presents two examples of using the theorem, noting that when two sides are given you square them and either add or subtract depending on whether the hypotenuse is known. Students are provided practice problems to solve for missing sides using the steps of writing the formula, substituting values, and solving the resulting equation for the unknown variable.

1. Pythagorean Theorem
Apply the Pythagorean Theorem to
determine unknown side lengths in right
triangles in real-world and mathematical
problems in two and three dimensions.

2. Today’s Objective
Today, we are going to learn how to use
the Pythagorean Theorem to solve for a
missing length of a right triangle.

3. Pythagorean Theorem
• What is the Pythagorean Theorem in
symbol form?
a2 + b2 = c2
• Which of these variables represent the
hypotenuse?
c
• Once you have figured out which is C,
does it matter which leg is A and which
is B?
no

4. Steps to Solve for a Missing
Side of a Triangle using the
Pythagorean Theorem
Step 1: Write the formula.
Step 2: Substitute known values for the variables.
Step 3: Solve the equation for the missing variable.

5. Example 1
Step 1: Write the formula
c
8 ft
15 ft
Find
c
a2 + b2 = c2
82 + 152 = c2Step 2: Substitute known values
Which number goes where?
• You need to identify the hypotenuse. It’s the one opposite of the
right angle.
• Does it matter whether we use a = 8 or 15? No.
Let’s use a = 8 and b = 15.
• The hypotenuse is always going to be the c in the formula. Since we
do not know the value of c, it stays as c in the formula.

6. Example 1
Step 1: Write the formula
x
8 ft
15 ft
Find
x
a2 + b2 = c2
82 + 152 = c2Step 2: Substitute known value
64 + 225 = c2
289 = c2
We are not done yet…
We have found c2, but
not just plain c.
Step 3: Solve for the missing
variable, in this case c.
289 = c2
17 = c

7. Try this one in your notes…..
x
5 ft
12 ft
Find x

8. Di
52 + 122 = x2
25 + 144 = x2
169 = x2
Answer x = 13
Did your work
look like this?

9. Example #2
x14 in
6 in
Find x.
Round to the nearest
hundredth.
Step 1: Write out the formula a2 + b2 = c2
a2 + 62 = 142Step 2: Substitute known values
Which number goes where?
This time we are given the hypotenuse.
Does it matter whether we use a = 6 or b = 6?
Let’s use b = 6.
So, c = 14
No

10. Example #2
x14 in
6 in
Find x.
Round to the nearest
hundredth.
Step 1: Write out the formula a2 + b2 = c2
a2 + 62 = 142
Step 2: Substitute known values
Step 3: Solve for the missing
variable, in this case a.
a2 + 36 = 196
Can we just add the two numbers and take the
square root? No, they are not on the same
side of the equals sign.
– 36 – 36
a2 = 160
a2 = 160
a = 12.64911
x = 12.65

11. What is the difference between
the 2 examples?
• Both have you squaring the given sides.
• Both have you using the square root at the
end.
• The only difference is in the middle.
– Example 1 has you adding the numbers
– Example 2 has you subtracting the smaller from
the larger.

12. What does this mean?
• When you have two sides of a right triangle, you
can find the third using the Pythagorean Theorem.
• Square both of the measurements you have.
• Add or subtract the two numbers depending on
whether or not you have the hypotenuse. (Subtract
if you have it, add if you don’t)
• Find the square root of the result and you have
your missing side!

13. Try this one in your notes…
15
20
x
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 25

14. Try this one in your notes…
7
12
x
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 13.89

15. Try this one in your notes…
3
x5
Answer: 4
Solve for x.
Round your answer to the nearest hundredth if necessary.

16. Try this one in your notes…
7
x
30
Answer: 30.81
Solve for x.
Round your answer to the nearest hundredth if necessary.

17. Try this one in your notes…
ab
c
Answer: D
If the hypotenuse of this triangle is 10 and a is 6 which
equation would you use to find b?
a) 6 + b = 10
b) 36 + b = 100
c) b2 – 36 = 100
d) 36 + b2 = 100

18. Please email me or call
me if you have any
difficulties working the
practice problems.