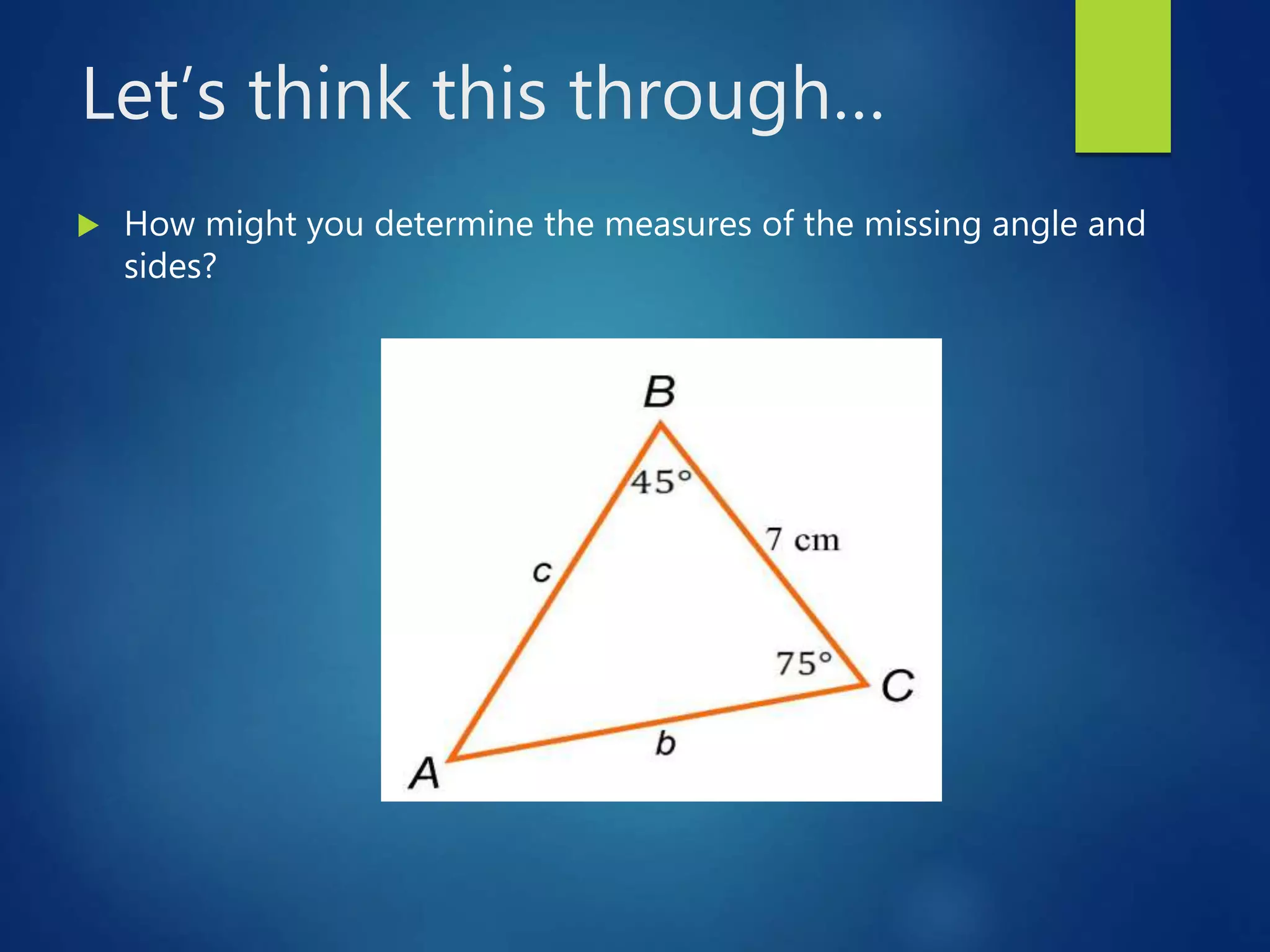
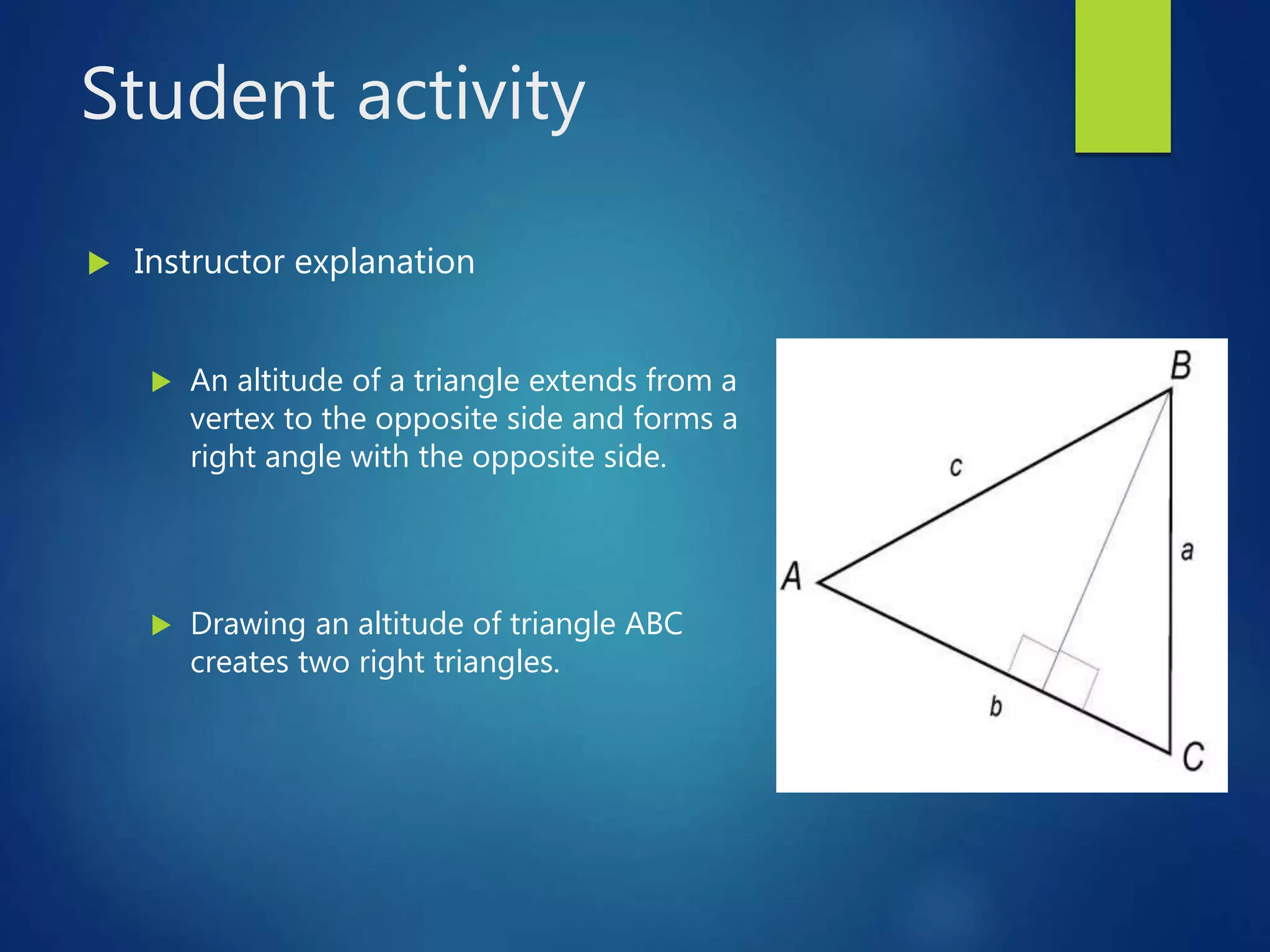
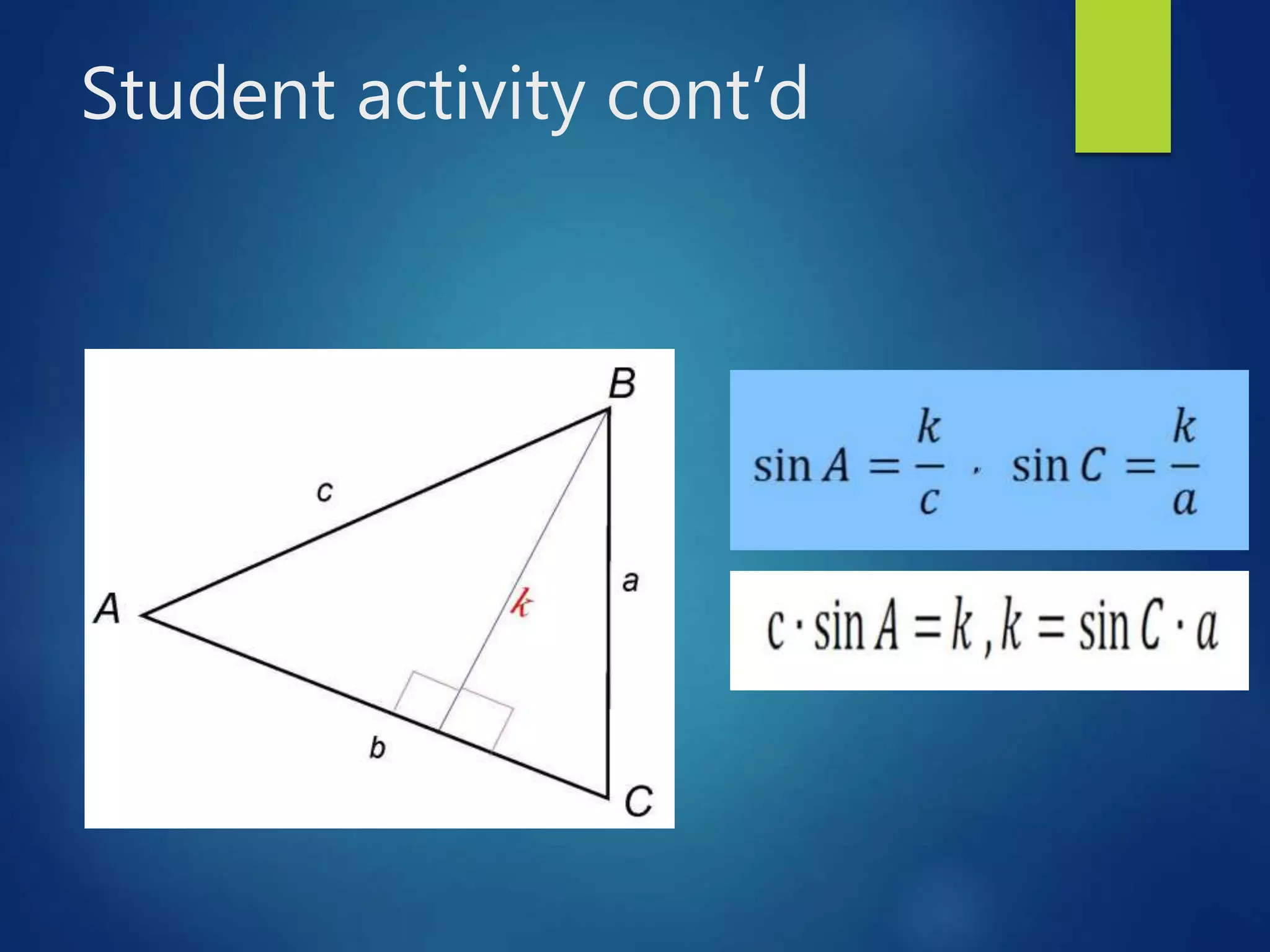
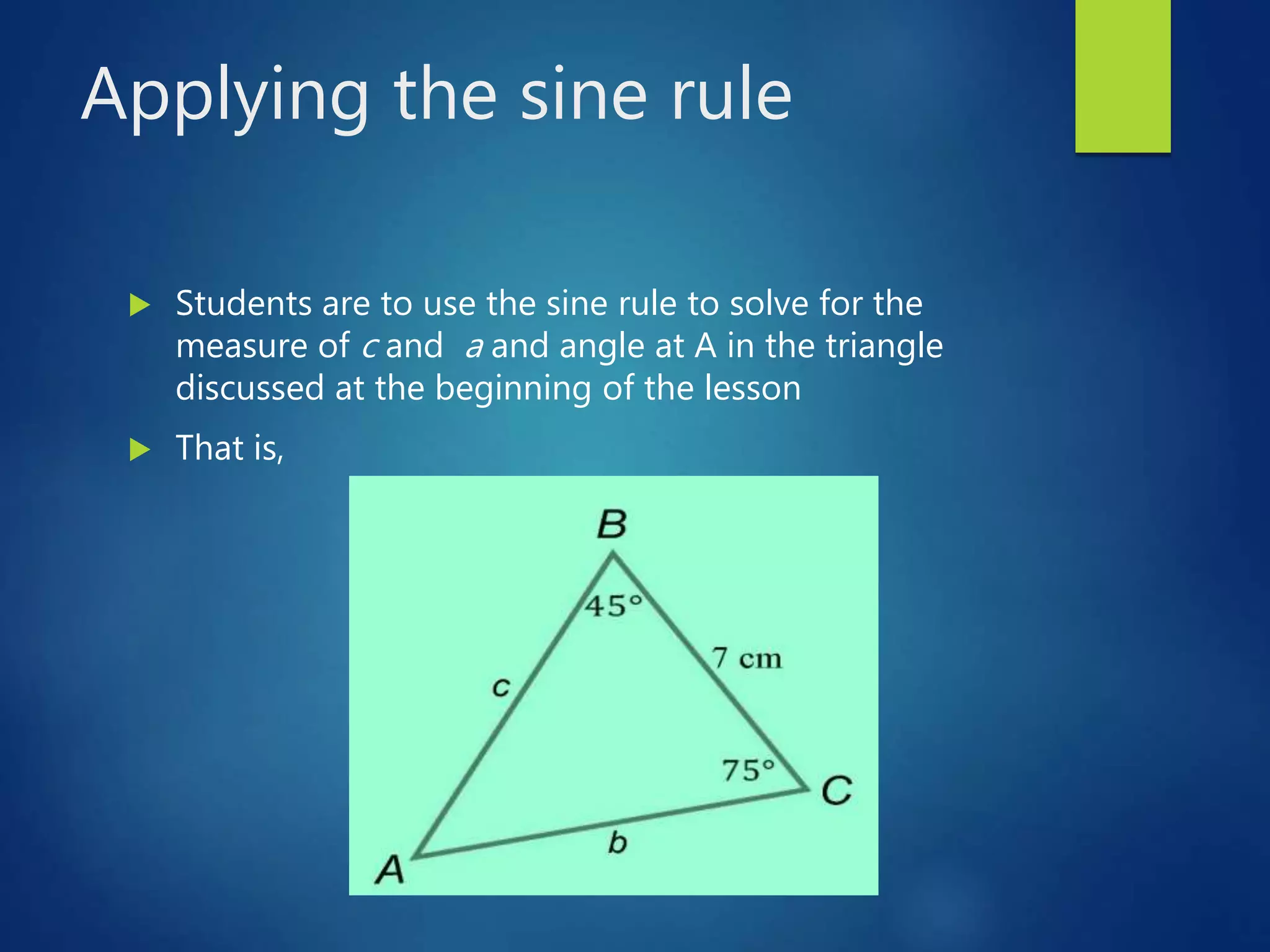
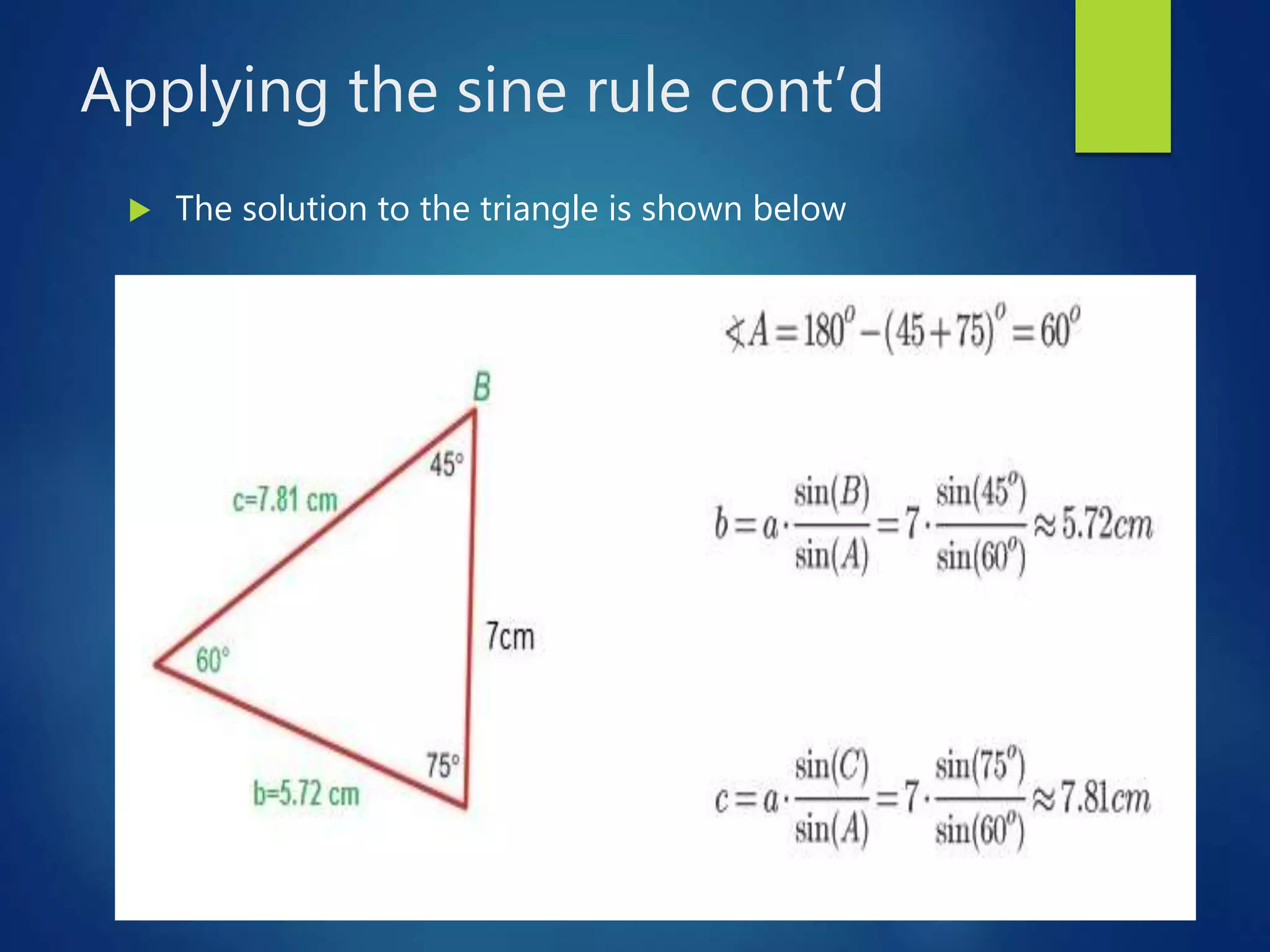
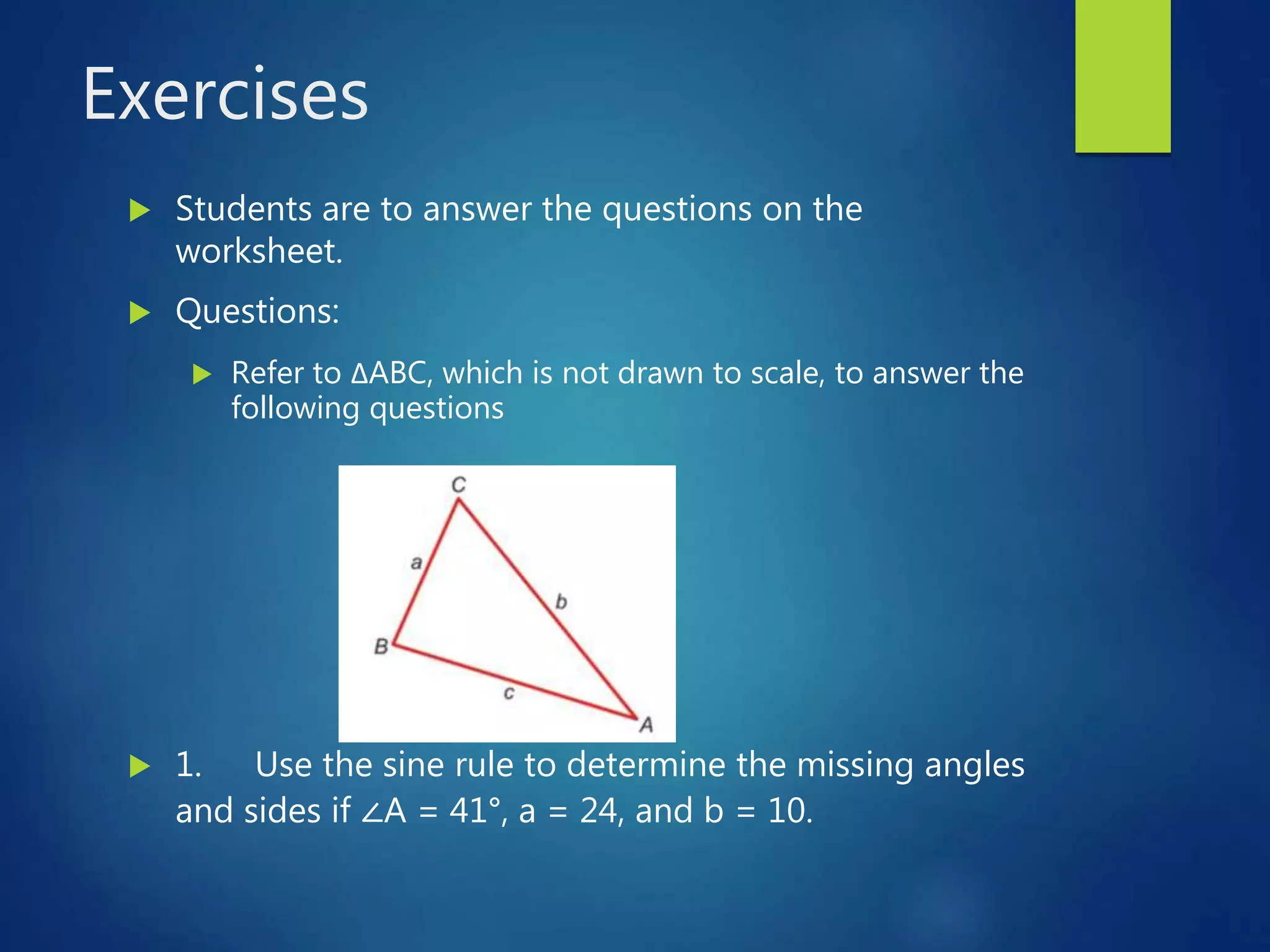
This document presents a lesson on deriving and applying the sine rule to solve for unknown angles and sides of triangles. It begins with discussing whether a unique triangle can be determined given certain angle and side measures. It then derives the sine rule by drawing altitudes in a triangle to form right triangles and using trigonometric relationships. Students practice using the sine rule to solve problems and check their work. The lesson emphasizes that the sine rule can be used to solve for missing values in triangles when one angle and two sides or all three sides are known.

1. Didactic Lesson
TRIGONOMETRY

2. Let’s think this through…
 Is there a unique triangle with the given angle and side measures?
Why?

3. Let’s think this through…
 How might you determine the measures of the missing angle and
sides?

4. Discussion
 The triangle is unique
 AAS is one method for proving that triangles are
congruent.
 Therefore, if two angles and a side are known, the
triangle is unique

5. Discussion cont’d
 Since the sum of the three angles in every triangle
is 180°, subtract the two angle measures from 180° to
determine the measure of the third angle.
 Finding the side lengths is more difficult…
 Finding a method for determining the side lengths (or
angles) of a unique triangle is the purpose of this
lesson.

6. Lesson Objectives
 Use right triangle trigonometry to develop
the sine rule
 Use the sine rule to solve problems.

7. Student activity
 Instructor explanation
 An altitude of a triangle extends from a
vertex to the opposite side and forms a
right angle with the opposite side.
 Drawing an altitude of triangle ABC
creates two right triangles.

8. Student activity cont’d
 Instructor explanation
 Since two right triangles are created, right triangle
trigonometry can be used to describe the relationships
between the angles and sides of each triangle.
 Because triangle ABC shares angles and sides with the
two right triangles, the relationships between the angles
and sides of the right triangles can be used to describe
the relationships between the angles and sides of
triangle ABC.

9. Student activity cont’d

10. Equations deduced
 𝑐. 𝑠𝑖𝑛𝐴 = 𝑎 ∙ 𝑠𝑖𝑛𝐶

𝑎
𝑠𝑖𝑛𝐴
=
𝑐
𝑠𝑖𝑛𝐶
−−− −(1)

11. Student activity (part 2)
 Instructor facilitation
 Students are to follow questions 7 to 13 and derive an equation for
the oblique triangle ABC
 Students then discusses their results with the instructor
 𝑐 ∙ 𝑠𝑖𝑛𝐵 = 𝑏 ∙ 𝑠𝑖𝑛𝐶

𝑏
𝑠𝑖𝑛𝐵
=
𝑐
𝑠𝑖𝑛𝐶
--------(2)

12. Student Activity cont’d
 Connecting equations
 Relating equation (1) and (2)

𝑎
𝑠𝑖𝑛𝐴
=
𝑏
𝑠𝑖𝑛𝐵
=
𝑐
𝑠𝑖𝑛𝐶
Sine Rule

13. Applying the sine rule
 Students are to use the sine rule to solve for the
measure of c and a and angle at A in the triangle
discussed at the beginning of the lesson
 That is,

14. Applying the sine rule cont’d
 The solution to the triangle is shown below

15. Exercises
 Students are to answer the questions on the
worksheet.
 Questions:
 Refer to ΔABC, which is not drawn to scale, to answer the
following questions
 1. Use the sine rule to determine the missing angles
and sides if ∠A = 41°, a = 24, and b = 10.

16. Exercises
 2. Use the sine rule to determine the missing angles
and sides if ∠A = 32°, a = 6.5 and b = 9.2.
 3. Use the law of sines to determine the missing
angles and sides if ∠B = 58°, a = 5, and b = 3.4.

17. Solutions to Exercise
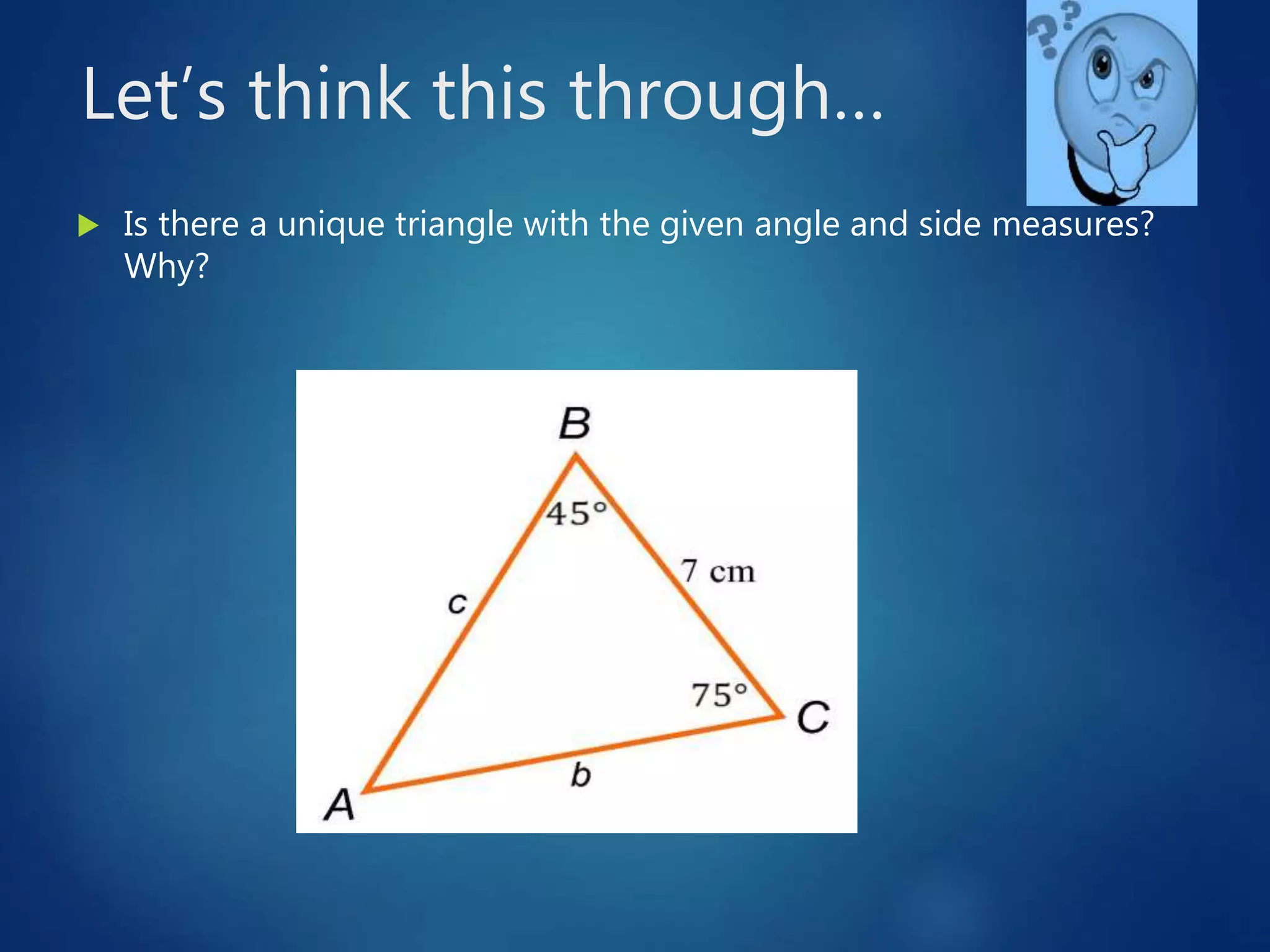
 [There is only one possible triangle. Although two
values, 15.86° and 164.14°, result for the measure of
∠B, the second answer is impossible. Therefore, ∠b =
15.86, ∠C = 123.14°, and c = 30.63]
 There are two possible triangles, because the measure
of ∠B could be either 48.59° or 131.41°. If ∠B = 48.59°,
then ∠C = 99.41° and c = 12.1. If ∠B = 131.41°, then
∠C = 16.59° and c = 3.5.
 There are no solutions, because the law of sines would
yield that sin A = (5 × sin 58°) / 3.4 = 1.2471, which is
impossible.]

18. Conclusion
 Instructor describes the importance of the sine rule, in
that it can be used to solve problems involving
non-right triangles.
 Instructor also emphasize that the sine rule cannot
solve all problems involving non-right triangles.
 E.g. If two angles and a side or two sides and a
non-included angle of a triangle are known, the law of
sines can be used to determine the missing angles and
sides of the triangle.

19. THANK YOU