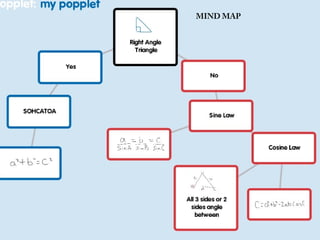
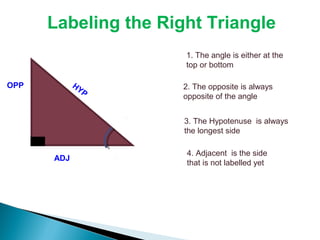
1. SOHCAHTOA is a mnemonic used to remember the definitions of the trigonometric ratios sine, cosine, and tangent in right triangles. 2. A right triangle has one 90 degree angle. The side opposite the right angle is called the hypotenuse. The other two sides are called the opposite and adjacent sides in relation to a given acute angle. 3. The trig ratios are defined as: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.

2. MIND MAP

3. SOHCAHTOA
1. You use Sin when you
have the opposite and
SOH = 0 Sin hypotenuse
H
2. You use Cos when you
have the adjacent and
hypotenuse
CAH = A Cos
H 3. You use Tan when you have the
opposite and the adjacent
TOA = O Tan
A

4. Labeling the Right Triangle
1. The angle is either at the
top or bottom
OPP HY 2. The opposite is always
P
opposite of the angle
3. The Hypotenuse is always
the longest side
4. Adjacent is the side
ADJ
that is not labelled yet

5. Trigonometry: The branch of mathematics concerned with the properties of triangles and calculations based on these
properties.
Acute Triangle : A triangle which all interior angles are acute angles
Obtuse Triangle : A triangle in which one of the angles is an obtuse angle that is an angle greater than 90 o and less than 180o
Right Triangle: A triangle with one right angle
Primary Trig Ratio : The basic ratios of trigonometry sine, cosine, tangent
Sine : is one of the primary trig ratios in a right angle triangle for opposite over hypotenuse
Sine Law : in any of triangle ABC with sides abc opposite angles A,B,C respectively
Cosine : is one of the primary trig ratios in a right angle triangle for adjacent over hypotenuse
Cosine Law: an equation used when a triangle does not have a right angle all 3 sides or 2 sides angle between
Law
Pythagorean theorem: in a right angle triangle the square of the length of the hypotenuse is equal to the sun of the square of
the squares of the lengths of the other two sides
Tangent: one of the primary trig ratios in a right angle triangle the ratio of the length of the side opposite angle to the length of
the adjacent side
Hypotenuse: In a right angle triangle the side opposite the right angle
Angle of Elevation: An angle measured from the horizontal plane upward from an observer's eye to a given point above the
plane
Angle of Depression : The angle measured below the horizontal that an observer must look to see an object that is lower than
the observer
Bearings: A bearing is an angle, measured clockwise from the north direction

6. An airplane is approaching a runway at an angle
of descent of 30o
What is the altitude of the airplane when it is 15
km along its flight path from the runway
H
yp
• Label The Triangle
15 • Decide which Trig
OPP km
Ratio will be used
• Sin, Cos, Tan
30o
Adj

7. 1. Use Tan because
where already have
H Hypotenuse and we
OPP yp want to find the
15km opposite
30o Tan 30o = O
2. Calculate Tan of 30
Adj A then cross multiply
Tan 30o = x 3. Multiply 0.5773
15 by 15
4. Gives you
0.5773 = x 8.67cm
15
Therefore, The altitude is
X=8.67cm 8.67com

8. Louise is a naturalist studying the effect of acid rain on fish population in
different lakes. As part of her research she needs to know the length of lake
Lebarge. Louise makes the measurements shown. How Long is the Lake.
A a = b = c Sin 320 x 340 = Sin 960c
96o
Sin A Sin B Sin C 0.5299 x 340 = 0.99452c
c b
180.17254 = 0.99452c
0.99452 0.99452
340 = b = c
520 32o 181. 2cm = c
B 340 cm C Sin 96 Sin 52 Sin 32
a Therefore, Lake Lebarge is
340 = c 181.2 cm long.
Sin 96 Sin 32 3. Multiply 0.5299 with 340 and
0.99452 with c
4. Divide both side by 0.99452
1. Fill in the correct information in the equation
2. Cross Multiply the 340 with sin of 32
and sin 96 with c

9. Angle S = 560
Length a = 14 cm
Length t = 25 cm
A Farmer is building a fence around his chicken pen
Find the perimeter of the Triangle SAT with the given lengths
and angles 1. Fill in all the angles
S2 = a2 + t2 – 2at Cos S and lengths
2. Do 14 squared and
S S2 = 142 + 252 – 2(14) (25) Cos 56 25 squared then
multiply -2 by 14 and 25
560 S2 = 196 + 625 – 700 Cos 56 3. Do Cos of 56o and
S2 = 196 + 625 – 700 0.5591 multiply it by 700
25cm 14cm
4. Add 196 and 625 then
S = 196 + 625 – 391.37
2
subtract 391.37
t a Square root 429.63 to give
S = 429. 63 you 20.7
S= 20.7 5. Add all the sides together to
give you the perimeter of 59.73
T
A s P=s+s+s
20cm
P= 25 + 14 + 20.7 Therefore, the perimeter of the
P = 59.73 triangle is 59.73

10. BY: Shehribane
Haziri