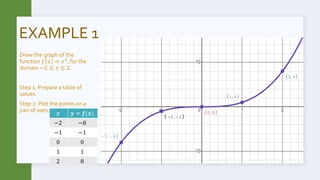
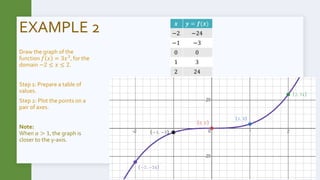
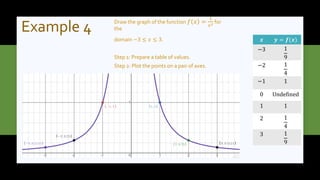
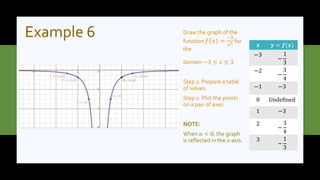
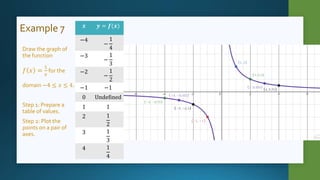
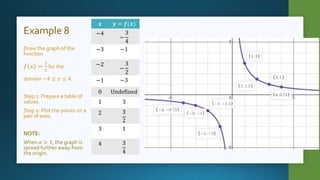
This document discusses non-linear functions of the form y=ax^n, where a is a constant and n is -1, -2, or 3. It provides examples of drawing graphs of cubic, square, and inverse functions by preparing tables of values and plotting points. The key effects of changing the constant a are noted - when a>1, the graph is spread further from the origin for squares and cubes or closer to the y-axis for cubes; when a<0, the graph is reflected across the x-axis for squares or y-axis for cubes and inverses. Step-by-step worked examples are given to illustrate graphing these types of functions.

1. GRAPHOF
NON-LINEARFUNCTIONS
𝒚 = 𝒂𝒙𝒏

2. 𝑦 = 𝑎𝑥𝑛
𝑛 = −1, −2, +3
𝑎 is a constant.
 𝑦 =
𝑎
𝑥
 𝑦 =
𝑎
𝑥2
 𝑦 = 𝑎𝑥3

3. LET’S DRAW SOME
GRAPHS!

4. 𝒚 = 𝒂𝒙𝟑
, 𝒂 is a constant.

5. EXAMPLE 1
Draw the graph of the
function 𝑓 𝑥 = 𝑥3
, for the
domain −2 ≤ 𝑥 ≤ 2.
Step 1: Prepare a table of
values.
Step 2: Plot the points on a
pair of axes.
𝒙 𝒚 = 𝒇(𝒙)
−2 −8
−1 −1
0 0
1 1
2 8

6. EXAMPLE 2
Draw the graph of the
function 𝑓 𝑥 = 3𝑥3, for the
domain −2 ≤ 𝑥 ≤ 2.
Step 1: Prepare a table of
values.
Step 2: Plot the points on a
pair of axes.
Note:
When 𝑎 > 1, the graph is
closer to the y-axis.
𝒙 𝒚 = 𝒇(𝒙)
−2 −24
−1 −3
0 0
1 3
2 24

7. EXAMPLE 3
Draw the graph of the
function 𝑓 𝑥 = −2𝑥3
,
for the domain −2 ≤
𝑥 ≤ 2.
Step 1: Prepare a table of
values.
Step 2: Plot the points on
a pair of axes.
𝒙 𝒚 = 𝒇(𝒙)
−2 16
−1 2
0 0
1 −2
2 −16
Note:
When 𝑎 < 0, the graph is reflected in the y-axis.

8. 𝒚 = 𝒂𝒙−𝟐
=
𝒂
𝒙𝟐 , 𝒂 is a constant.

9. Example 4 Draw the graph of the function 𝑓 𝑥 =
1
𝑥2 for
the
domain −3 ≤ 𝑥 ≤ 3.
Step 1: Prepare a table of values.
Step 2: Plot the points on a pair of axes.
𝒙 𝒚 = 𝒇(𝒙)
−3 1
9
−2 1
4
−1 1
0 Undefined
1 1
2 1
4
3 1
9

10. Example 5
Draw the graph of the function 𝑓 𝑥 =
2
𝑥2 for the domain −3 ≤ 𝑥 ≤ 3.
Step 1: Prepare a table of values.
Step 2: Plot the points on a pair of axes.
NOTE:
When 𝑎 > 1, the graph is spread further away from the origin.
𝒙 𝒚 = 𝒇(𝒙)
−3 2
9
−2 1
2
−1 2
0 Undefined
1 2
2 1
2
3 2
9

11. Example 6 Draw the graph of the
function 𝑓 𝑥 =
−3
𝑥2 for
the
domain −3 ≤ 𝑥 ≤ 3.
Step 1: Prepare a table
of values.
Step 2: Plot the points
on a pair of axes.
NOTE:
When 𝑎 < 0, the graph
is reflected in the x-axis.
𝒙 𝒚 = 𝒇(𝒙)
−3
−
1
3
−2
−
3
4
−1 −3
0 Undefined
1 −3
2
−
3
4
3
−
1
3

12. 𝒚 = 𝒂𝒙−𝟏
=
𝒂
𝒙
, 𝒂 is a constant.

13. Example 7
Draw the graph of
the function
𝑓 𝑥 =
1
𝑥
for the
domain −4 ≤ 𝑥 ≤ 4.
Step 1: Prepare a
table of values.
Step 2: Plot the
points on a pair of
axes.
𝒙 𝒚 = 𝒇(𝒙)
−4
−
1
4
−3
−
1
3
−2
−
1
2
−1 −1
0 Undefined
1 1
2 1
2
3 1
3
4 1
4

14. Example 8
Draw the graph of the
function
𝑓 𝑥 =
3
𝑥
for the
domain −4 ≤ 𝑥 ≤ 4.
Step 1: Prepare a table of
values.
Step 2: Plot the points on a
pair of axes.
NOTE:
When 𝑎 > 1, the graph is
spread further away from
the origin.
𝒙 𝒚 = 𝒇(𝒙)
−4
−
3
4
−3 −1
−2
−
3
2
−1 −3
0 Undefined
1 3
2 3
2
3 1
4 3
4

15. Example 9
Draw the graph of the
function
𝑓 𝑥 =
−2
𝑥
for the
domain −4 ≤ 𝑥 ≤ 4.
Step 1: Prepare a table of
values.
Step 2: Plot the points on a
pair of axes.
NOTE:
When 𝑎 < 0, the graph is
reflected in the y-axis.
𝒙 𝒚 = 𝒇(𝒙)
−4 1
2
−3 2
3
−2 1
−1 2
0 Undefined
1 −2
2 −1
3
−
2
3
4
−
1
2

16. The End.