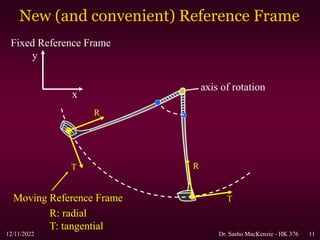
This document provides an overview of angular kinematics concepts including angular displacement, velocity, acceleration, centripetal acceleration, and tangential acceleration. Examples are presented to demonstrate how to calculate these quantities for objects moving in circular motion, including a runner running a curved track segment and cyclists rounding a turn. Key relationships between linear and angular motion are also summarized, such as how linear velocity depends on angular velocity and radius.

1. 12/11/2022 Dr. Sasho MacKenzie - HK 376 1
Angular Kinematics
Angular motion occurs when all points
on an object move in circular paths
about the same fixed axis.
Chapter 6 in the text

2. 12/11/2022 Dr. Sasho MacKenzie - HK 376 2
KINEMATICS
LINEAR ANGULAR
Scalars
Distance
Speed
Vectors
Displacement
Velocity
Acceleration
Previous Class

3. 12/11/2022 Dr. Sasho MacKenzie - HK 376 3
What is an angle?
• An angle is formed by the intersection of
two lines.
• The symbol for angle is  (Theta).
• Angles can be measured in degrees or
radians (rads). 1 rad = 180/Pi = 57.3

4. 12/11/2022 Dr. Sasho MacKenzie - HK 376 4
Angular Displacement

Angular displacement (rads)
Angular displacement is the change in angular position
experienced by a rotating line. A vector quantity.
radius
r
L


radius
length
c
ar


Arc length

5. 12/11/2022 Dr. Sasho MacKenzie - HK 376 5
Direction of an angular vector
• Not like linear vectors. Angular vectors are
perpendicular to the plane of motion.
• Must use right hand rule
– Curl fingers of rt. hand in the direction of rotation.
– The direction of your extended thumb is the
direction of the angular displacement vector.
• A counterclockwise finger curl means the
thumb is pointing in the positive direction

6. 12/11/2022 Dr. Sasho MacKenzie - HK 376 6
Link between Linear Distance
and Angular Displacement
• Radius is the link between linear and
angular kinematics
• If the angular displacement is measured in
radians, then the linear distance (arc
length) is equal to the angular
displacement times the radius.
• L = *r

7. 12/11/2022 Dr. Sasho MacKenzie - HK 376 7
Angular Velocity
• The rate of change of angular displacement.
• Average angular velocity equals angular
displacement divided time.
• The symbol is  (omega).
• Angular velocity is a vector found using the
rt. hand rule.
t






8. 12/11/2022 Dr. Sasho MacKenzie - HK 376 8
Angular Distance and Angular Speed
• Angular distance and angular speed
define a magnitude of rotation but no
direction as they are scalar quantities.

9. 12/11/2022 Dr. Sasho MacKenzie - HK 376 9
Link between Linear and
Angular Velocity
• The link is radius.
• All points on a golf club undergo the same
angular displacement and therefore the
same angular velocity.
• But they trace out different arc lengths
based on their radius, therefore their linear
velocities must be different.

10. 12/11/2022 Dr. Sasho MacKenzie - HK 376 10
Points on Golf Club
The clubhead moves a longer
distance (arc length) in the same
time. Therefore, it must have a
higher linear velocity.
The longer the
club, the faster
the linear
velocity of the
head.
VT
axis of rotation
The instantaneous linear velocity (VT) is equal to
the instantaneous angular velocity times the
radius. VT , the instantaneous speed, is at a
tangent to the clubhead path.
r
VT 


11. 12/11/2022 Dr. Sasho MacKenzie - HK 376 11
New (and convenient) Reference Frame
x
y
Fixed Reference Frame
axis of rotation
R
T R
T
Moving Reference Frame
R: radial
T: tangential

12. 12/11/2022 Dr. Sasho MacKenzie - HK 376 12
Angular Acceleration
• The rate of change of angular velocity.
• Average angular acceleration equals the
change in angular velocity divided by time.
• The symbol is , (alpha)
• Angular acceleration is a vector found
using the rt. hand rule.
t






13. 12/11/2022 Dr. Sasho MacKenzie - HK 376 13
Angular Acceleration
• Angular acceleration occurs when
something spins faster and faster or slower
and slower, or when the object’s axis of
spin changes direction.

14. Track Example
12/11/2022 Dr. Sasho MacKenzie - HK 376 14
Usain Bolt runs the curve of this 200 m in 11 s. Assume he ran on the
inside line of lane 1, which makes a semicircle (r = 36.5 m) for the first
part of the race. His speed after the curve was 11.5 m/s.
36.5 m
1. What distance was run on the curve?
2. What was his angular displacement ?
3. What was his average angular velocity?
4. What was his average angular acceleration?
N
W E
S
Start
Finish
Circle Circumference = 2r; Circle Diameter = 2r; r is radius

15. 12/11/2022 Dr. Sasho MacKenzie - HK 376 15
Figure Skater Examples
1. While spinning in the air, a figure skater completes 400
degrees of rotation. What was the skater’s angular
displacement covered in radians? What was the
skater’s angular distance covered in radians?
2. If a figure skater has an initial angular velocity of 12
radians/second and undergoes an angular acceleration
of 10 radians/second/second for 0.5 seconds, what is
the skater’s final angular velocity?

16. 12/11/2022 Dr. Sasho MacKenzie - HK 376 16
Linear Acceleration and Rotation
When an object has angular motion, it is often
easier to express linear acceleration relative to a
reference frame that moves with the object.
So, instead of describing acceleration in the fixed X
and Y directions, we consider…
• Centripetal (radial) acceleration
– Calculated using angular velocity
• Tangential acceleration
– Calculated using angular acceleration

17. 12/11/2022 Dr. Sasho MacKenzie - HK 376 17
Centripetal Acceleration
• The component of linear acceleration directed
towards the axis of rotation (center of the
circle).
• Associated with the change in direction of an
object moving in a circle. Changes the
direction of the velocity vector (arrow).
r
v
a T
R
2
 r
aR
2



18. 12/11/2022 Dr. Sasho MacKenzie - HK 376 18
Centripetal Acceleration and VT
r

Vi
Vf
Vf = Vi + V
Vi
V
Vf
Resultant
Vector
Caused by radial
acceleration
aR
(VT)
(VT)

19. 12/11/2022 Dr. Sasho MacKenzie - HK 376 19
Tangential Acceleration
• The component of linear acceleration tangent to
the circular path (perpendicular to the radius).
• Associated with the speeding up of an object
moving in a circle. Increases the length of the
tangential velocity arrow.
• Equal to the angular acceleration times the
radius.
r
aT 


20. 12/11/2022 Dr. Sasho MacKenzie - HK 376 20
Constant Angular Motion
 = 0, therefore  is constant
at = 0, therefore Vt is constant
r = 2 m
 = 360 º (6.28 rad)
t = 3 s
For this example, instantaneous values
are the same as average values!

21. 12/11/2022 Dr. Sasho MacKenzie - HK 376 21
Accelerated Angular Motion
True or False
1. Between A and B,  is > 0?
2. Between D and A,  is > 0?
3. Omega () is always  0?
r = 2 m
 = 360 º (6.28 rad)
t = 3 s
Instantaneous values are
different than average values!
A
D
B
C
T
F
T

22. 12/11/2022 Dr. Sasho MacKenzie - HK 376 22
Visual Comparison
A
Which has/have the…
1. greatest ?
2. greatest Vt?
3. greatest aR?
4. smallest magnitude of at?
B C
B
C
C
A and C

23. 12/11/2022 Dr. Sasho MacKenzie - HK 376 23
Angular Kinematics Summary
Angular Displacement
Angular Velocity
Angular Acceleration
Centripetal Acceleration
Tangential Acceleration
Linear
Angular

24. Track Example #2
12/11/2022 Dr. Sasho MacKenzie - HK 376 24
At 4 s into his 200 m race, Bolt is running with a speed of 7 m/s. At 9 s,
his speed is at 10 m/s. Assume he is running on the inside line of lane 1,
which makes a semicircle (r = 36.5 m).
36.5 m
1. What’s his radial acceleration at 4 s?
2. What’s his radial acceleration at 9 s?
3. What’s his angular velocity at 4 s?
4. What’s his angular velocity at 9 s?
5. What’s his average angular acceleration
between 4 s and 9 s?
6. What’s his average tangential acceleration
between 4 s and 9 s?
N
W E
S
Start
Finish
t = 4s
t = 9 s

25. 12/11/2022 Dr. Sasho MacKenzie - HK 376 25
Example Problem
• The cyclists shown on the next page are rounding a turn
at the bottom of a hill. The path they follow in doing this
is a gentle curve that becomes progressively sharper as
they near the corner. The radius of the path followed by
one of these riders is 20 m at one point in the initial
gentle part of the turn, and then decreases to a
minimum value of 17 m, 1.5 s later. Her tangential
velocity at these two instants are 12 m/s and 11.5 m/s
respectively. What is her radial acceleration at the two
points? What is her average tangential acceleration
between the two points?

26. 12/11/2022 Dr. Sasho MacKenzie - HK 376 26
Biking On a Curve