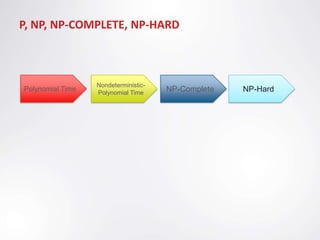
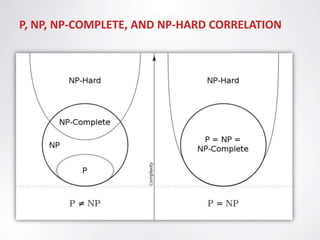
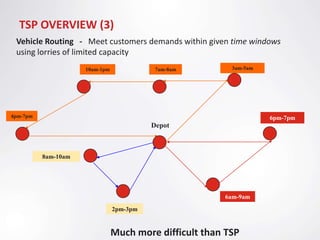
The document discusses the Travelling Salesman Problem (TSP), which aims to find the shortest route to visit each city in a list exactly once and return to the origin city. It describes TSP as an NP-hard problem, belonging to the complexity class NP-complete. The document provides background on TSP, explaining it cannot be solved in polynomial time using techniques like linear programming. While an efficient solution to the general TSP has not been found, there are approximation algorithms that provide near-optimal solutions.

1. Travelling Salesman Problem
Chapter 1 & 2
Raditya W Erlangga (G651120714)
Jemy Arieswanto (G651120664)
Amalia Rahmawati (G651120634)
Bogor, February 16th 2013

2. AGENDA
• Introduction
• NP-Complete Overview
• TSP
•Q&A

3. TRAVELLING SALESMAN
PROBLEM
Find the shortest possible route
that visits each city exactly once
and returns to the origin city
SECURITY UPDATE
<ISC SA or IR Number>
<Date>

4. P, NP, NP-COMPLETE, NP-HARD
Nondeterministic-
Polynomial Time Polynomial Time NP-Complete NP-Hard

5. P (POLYNOMIAL TIME)
» P is the set of all decision problems which can be solved in polynomial
time by a deterministic Turing machine. Since it can be solved in
polynomial time, it can also be verified in polynomial time
» E.g:
• Linear Programming -> determining a way to achieve the best
outcome (such as maximum profit or lowest cost) in a given
mathematical model
• finding Maximum Matching -> graph matching

6. NP (NON-DETERMINISTIC POLYNOMIAL)
» NP is the set of all decision problems (question with yes-or-no answer)
for which the 'yes'-answers can be verified in polynomial time (O(nk)
where n is the problem size, and k is a constant) by a deterministic
Turing machine. Polynomial time is sometimes used as the definition of
fast or quickly
» P is a subset of NP
» E.g:
• TSP

7. NP-COMPLETE
» A problem x that is in NP is also in NP-Complete if and only if every
other problem in NP can be quickly (ie. in polynomial time)
transformed into x. In other words:
• x is in NP, and
• Every problem in NP is reducible to x
» So what makes NP-Complete so interesting is that if any one of the NP-
Complete problems was to be solved quickly then all NP problems can
be solved quickly
» E.g:
• TSP

8. NP-HARD
» NP-Hard are problems that are at least as hard as the hardest problems
in NP. Note that NP-Complete problems are also NP-hard. However not
all NP-hard problems are NP (or even a decision problem), despite
having 'NP' as a prefix. That is the NP in NP-hard does not mean 'non-
deterministic polynomial time’
» E.g:
• TSP

9. P, NP, NP-COMPLETE, AND NP-HARD CORRELATION

10. TSP IS NP-HARD
U$ 1m
IF P = NP IS SOLVED
Millenium Prize
Problem
AND CREDITS FROM
SCIENTISTS AROUND
THE WORLD
source: http://www.claymath.org/millennium/P_vs_NP/

11. TSP HISTORY
» 1920: Karl Menger introduced the concept to colleagues in Vienna
» 1930: Intensive discussion in math community in Princeton University
» 1940: Merrill Meeks Flood publicized TSP to mass
» 1948: Flood presented TSP to RAND Corp. RAND is a non-profit
organization that focuses in intellectual research and development
within the US
» 1950: Linear Programming was becoming a vital force in computing
solutions to combinatorial optimization problems. The US Airforce
needed the method to optimize solutions of their combinatorial
transportation problem
» 1960’s: The TSP could not be solved in polynomial time using Linear
Programming techniques

12. TSP has never been
solved
by scientists and experts so far

13. TSP OVERVIEW (1)
» Find the shortest possible route that visits each city exactly once and
returns to the origin city -> Hamiltonian cycle
» Posed such computational complexity that any programmable efforts
to solve such problems would grow superpolynomially with the
problem size
» Can be used in :
• transportation: school bus routes, service calls, delivering meals
• manufacturing: an industrial robot that drills holes in printed
circuit boards
• VLSI (microchip) layout
• communication: planning new telecommunication networks

14. TSP OVERVIEW (2)
» One way to solve TSP is to use exhaustive search to find all possible
combinations of the next city to visit
» However, the method is costly, since the number of possible tours of a map
with n cities is (n − 1)! / 2
#cities #tours
5 12
6 60
7 360
8 2,520
9 20,160
10 181,440
» 25 cities will require:
310,224,200,866,619,719,680,000

15. TSP OVERVIEW (3)
Vehicle Routing - Meet customers demands within given time windows
using lorries of limited capacity
10am-1pm 7am-8am 3am-5am
4pm-7pm 6pm-7pm
Depot
8am-10am
6am-9am
2pm-3pm
Much more difficult than TSP

16. TSP OVERVIEW (4)
» Until this very day, an efficient solution to the general case TSP, or even
to any of its NP-hard variations, has not been found
» However, there are approximation solutions to solve the TSP:
• Polynomial Time Approximation Scheme (PTAS)
• Christofides Algorithm
• Double MST Algorithm
• Arora’s Algorithm
• Mitchell’s Algorithm

17. QUESTIONS?

18. THANK YOU