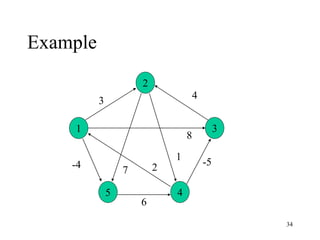
The document discusses various shortest path algorithms, including Dijkstra's and Bellman-Ford, for finding shortest paths in graphs. It explains the concepts of single-source shortest path problems and variations such as single-pair and all-pairs shortest paths, along with methods for graphs with negative weights. Additionally, it outlines the Floyd-Warshall algorithm and its matrix multiplication approach for computing all-pairs shortest paths.

1. 8/3/2020
SHORTEST PATH PROBLEM
Er. Pooja Saini
(spst.08@gmail.com)
Ambala College of Engineering and Applied Research, Ambala

2. 8/3/2020
SINGLE-SOURCE SHORTEST PATH

3. 8/3/2020
Introduction
Weight of path p = v1  v2  …  vk is
1
1
1
( ) ( , )
k
i i
i
w p w v v



 

4. 8/3/2020
Shortest Path
Shortest Path = Path of minimum weight
δ(u,v)= min{ω(p) : u v}; if there is a path from u to v,
 otherwise.
p

5. 8/3/2020
Shortest-Path Variants
• Shortest-Path problems
– Single-source shortest-paths problem: Find the shortest path from s
to each vertex v.
– Single-destination shortest-paths problem: Find a shortest path to a
given destination vertex t from each vertex v.
– Single-pair shortest-path problem: Find a shortest path from u to v
for given vertices u and v.
– All-pairs shortest-paths problem: Find a shortest path from u to v
for every pair of vertices u and v.

6. 8/3/2020
Relaxation
RELAX(u, v)
if d[v] > d[u]+w(u,v) then
d[v] ← d[u]+w(u,v)
π[v] ← u
5
u v
vu
2
2
9
5 7
Relax(u,v)
5
u v
vu
2
2
6
5 6

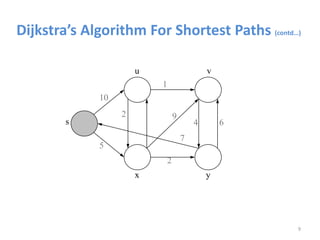
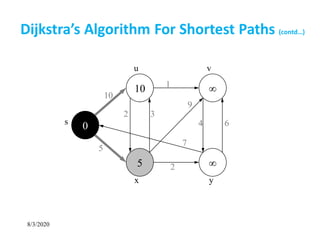
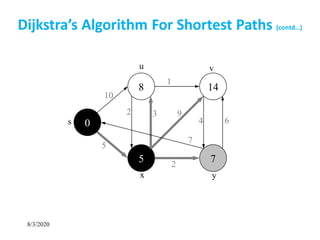
7. 8/3/2020
• Non-negative edge weight
• Use Q = priority queue keyed on d[v] values
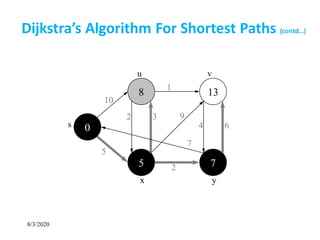
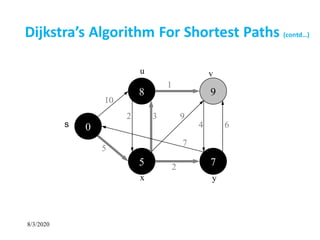
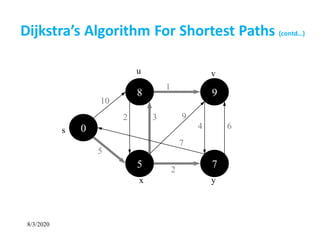
Dijkstra’s Algorithm For Shortest Paths

8. 8
• Graph G, weight function w, root s
relaxing
edges
Dijkstra’s Algorithm For Shortest Paths

9. 9
s
u v
yx
10
5
1
2 9
4 6
7
2
Dijkstra’s Algorithm For Shortest Paths (contd…)

10. 8/3/2020
3
 
 
0s
u v
yx
10
5
1
2 9
4 6
7
2
Dijkstra’s Algorithm For Shortest Paths (contd…)

11. 8/3/2020
2
10 
5 
0s
u v
yx
10
5
1
3
9
4 6
7
2

12. 8/3/2020
2
8 14
5 7
0s
yx
10
5
1
3 9
4 6
7
2
u v

13. 8/3/2020
10
8 13
5 7
0s
u v
yx
5
1
2 3 9
4 6
7
2

14. 8/3/2020
8
u v
9
5 7
0
yx
10
5
1
2 3 9
4 6
7
2
s

15. 8/3/2020
u
5
8 9
5 7
0
v
yx
10
1
2 3 9
4 6
7
2
s

16. 8/3/2020
Observe :
• Each vertex is extracted from Q and inserted into S
exactly once
• Each edge is relaxed exactly once
• S = set of vertices whose final shortest paths have already
been determined
 i.e. , S = {v  V: d[v] = δ(s, v) ≠ ∞ }
Dijkstra’s Algorithm For Shortest Paths

17. 8/3/2020
Bellman-Ford Algorithm for Single
Source Shortest Paths
• More general than Dijkstra’s algorithm
- Edge-weights can be negative.
• Detects the existence of negative-weight cycle(s)
reachable from s.

18. 8/3/2020
Negative-weight edges
• No problem, as long as no negative-weight cycles are
reachable from the source
• Otherwise, we can just keep going around it, and
get w(s, v) = −∞ for all v on the cycle.

19. 8/3/2020
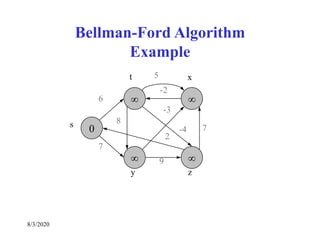
BELMAN-FORD( G, w, s )
INIT( G, s )
for i ←1 to |V|-1 do
for each edge (u, v)  E do
RELAX( u, v )
for each edge ( u, v )  E do
if d[v] > d[u]+w(u,v) then
return FALSE > neg-weight cycle
return TRUE
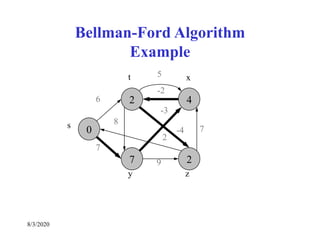
Bellman-Ford Algorithm for Single
Source Shortest Paths

20. 8/3/2020
Bellman-Ford Algorithm
Example
5
 
 
0s
zy
6
7
8
-3
7
2
9
-2
xt
-4

21. 8/3/2020
Bellman-Ford Algorithm
Example
2 4
7 2
0s
zy
6
7
8
-3
7
2
9
-2
xt
-4
5

22. 8/3/2020
Single-Source Shortest Paths in DAGs
• Shortest paths are always well-defined in dags
 no cycles => no negative-weight cycles even if
there are negative-weight edges

23. 8/3/2020
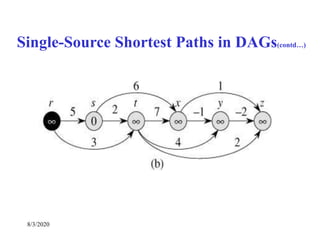
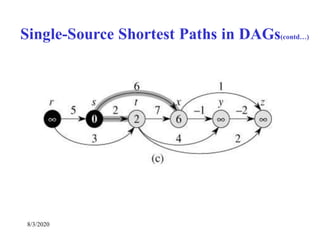
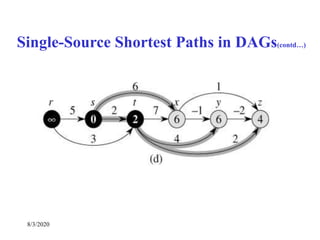
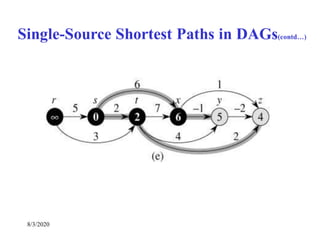
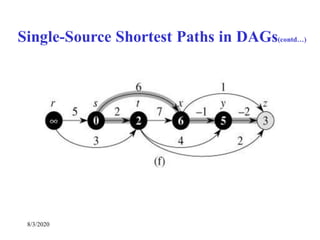
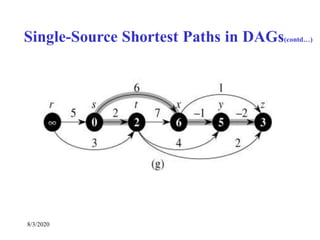
Single-Source Shortest Paths in DAGs
DAG-SHORTEST PATHS(G, s)
TOPOLOGICALLY-SORT the vertices of G
INIT(G, s)
for each vertex u taken in topologically sorted order do
for each v  Adj[u] do
RELAX(u, v)

24. 8/3/2020
Single-Source Shortest Paths in DAGs(contd…)

25. 8/3/2020

26. 8/3/2020
Single-Source Shortest Paths in DAGs(contd…)

27. 8/3/2020

28. 8/3/2020

29. 8/3/2020

30. 8/3/2020
EXTEND-SHORTEST-PATHS(D,W)
n = rows[D]
let D' = (d'ij) be an n * n matrix
for i = 1 to n do
for j = 1 to n do
d'ij = ∞
for k = 1 to n do
d'ij = min(d'ij, dik + wkj)
return D'
Shortest Path and Matrix Multiplication

31. 8/3/2020
SLOW-ALL-PAIRS-SHORTEST-PATHS(W)
n = rows[W]
D(1) = W
for m = 2 to n – 1
D(m) = EXTEND-SHORTEST-PATHS(D(m-1),W)
return D(n-1)

32. 32
• Let dij
(k) be the weight of a shortest path from vertex i to
vertex j with all intermediate vertices in the set {1,2,…,k}.
A recursive definition is given by
• dij
(k)= wij if k=0,
• min(dij
(k-1),dik
(k-1)+dkj
(k-1)) if k 1.
• The matrix D(n)=(dij
(n)) gives the final answer-dij
(n)=
for all i,j V-because all intermediate vertices are in the
set {1,2,…,n}.
 
),( ji


33. 33
• FLOYD-WARSHALL(W)
n rows[W]
D(0) W
for k 1 to n
do for i 1 to n
do for j 1 to n
dij
(k) min(dij
(k-1),dik
(k-1)+dkj
(k-1))
return D(n)







34. 34
Example
1
5 4
3
2
3 4
7
-4
8
1 -5
2
6

35. 35





















06
052
04
710
4830
D(0)=
















NILNILNILNIL
NILNILNIL
NILNILNILNIL
NILNILNIL
NILNIL
5
44
3
22
111
(0)=
D(1)=
(1)=





















06
20552
04
710
4830


















NILNILNILNIL
NIL
NILNILNILNIL
NILNILNIL
NILNIL
5
1414
3
22
111

36. 36





















06
20552
11504
710
44830
D(2)=
















NILNILNILNIL
NIL
NILNIL
NILNILNIL
NIL
5
1414
223
22
1211
(2)=
D(3)=
(3)=





















06
20512
11504
710
44830


















NILNILNILNIL
NIL
NILNIL
NILNILNIL
NIL
5
1434
223
22
1211

37. 37



















06158
20512
35047
11403
44130
D(4)=
















NIL
NIL
NIL
NIL
NIL
5434
1434
1234
1244
1241
(4)=
D(5)=
(5)=



















06158
20512
35047
11403
42310


















NIL
NIL
NIL
NIL
NIL
5434
1434
1234
1244
1543