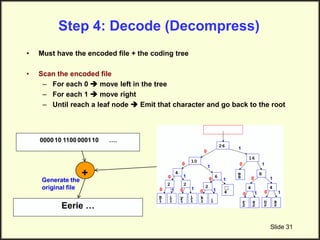
Huffman coding is an efficient lossless data compression technique that reduces file sizes by encoding characters based on their frequency of occurrence, achieving between 20%-90% compression. It involves creating a binary tree where more common characters receive shorter codes and less common characters receive longer codes, ensuring unique decoding. The process includes scanning for character frequencies, building a Huffman tree, encoding the original file using the tree, and decoding it back to its original form.

1. Greedy Algorithms
(Huffman Coding)
Slide 1

2. Huffman Coding
• A technique to compress data effectively
– Usually between 20%-90% compression
• Lossless compression
– No information is lost
– When decompress, you get the original file
Slide 2
Original file
Compressed file
Huffman coding

3. Huffman Coding: Applications
• Saving space
– Store compressed files instead of original files
• Transmitting files or data
– Send compressed data to save transmission time and power
• Encryption and decryption
– Cannot read the compressed file without knowing the “key”
Slide 3
Original file
Compressed file
Huffman coding

4. Main Idea: Frequency-Based Encoding
• Assume in this file only 6 characters appear
– E, A, C, T, K, N
• The frequencies are: Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
• Option I (No Compression)
– Each character = 1 Byte (8 bits)
– Total file size = 14,700 * 8 = 117,600 bits
• Option 2 (Fixed size compression)
– We have 6 characters, so we need
3 bits to encode them
– Total file size = 14,700 * 3 = 44,100 bits
Character Fixed Encoding
E 000
A 001
C 010
T 100
K 110
N 111

5. Main Idea: Frequency-Based Encoding
(Cont’d)
• Assume in this file only 6 characters appear
– E, A, C, T, K, N
• The frequencies are: Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
• Option 3 (Huffman compression)
– Variable-length compression
– Assign shorter codes to more frequent characters and
longer codes to less frequent characters
– Total file size:
Char. HuffmanEncoding
E 0
A 10
C 110
T 1110
K 11110
N 11111
(10,000 x 1) + (4,000 x 2) + (300 x 3) + (200 x 4) + (100 x
5) + (100 x 5) = 20,700 bits

6. Huffman Coding
• A variable-length coding for characters
– More frequent characters  shorter codes
– Less frequent characters  longer codes
• It is not like ASCII coding where all characters have the
same coding length (8 bits)
• Two main questions
– How to assign codes (Encoding process)?
– How to decode (from the compressed file, generate the
original file) (Decoding process)?
Slide 6

7. Decoding for fixed-length codes is
much easier
Slide 7
Character Fixed-length
Encoding
E 000
A 001
C 010
T 100
K 110
N 111
010001100110111000
010 001 100 110 111 000
Divide into 3’s
C A T K N E
Decode

8. Decoding for variable-length codes is
not that easy…
Slide 8
Character Variable-length
Encoding
E 0
A 00
C 001
… …
… …
… …
000001
It means what???
EEEC EAC AEC
Huffman encoding guarantees to avoid this
uncertainty …Always have a single decoding

9. Huffman Algorithm
• Step 1: Get Frequencies
– Scan the file to be compressed and count the occurrence of
each character
– Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
– Build a Huffman-code tree (binary tree)
– Traverse the tree to assign codes
• Step 3: Encode (Compress)
– Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
– Huffman tree is the key to decompress the file
Slide 9

10. Step 1: Get Frequencies
Slide 10
Eerie eyes seen near lake.
Char Freq. Char Freq. Char Freq.
E 1 y 1 k 1
e 8 s 2 . 1
r 2 n 2
i 1 a 2
space 4 l 1
Input File:

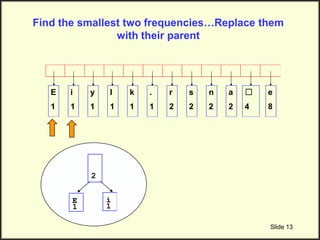
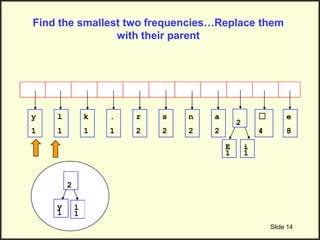
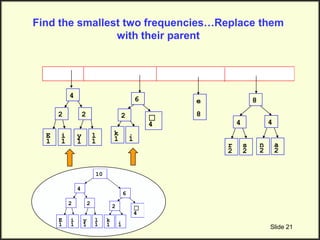
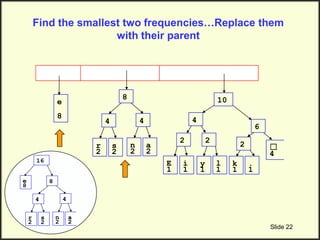
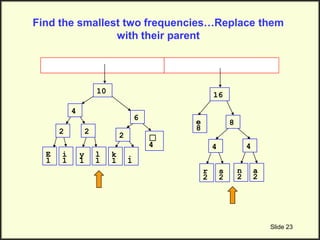
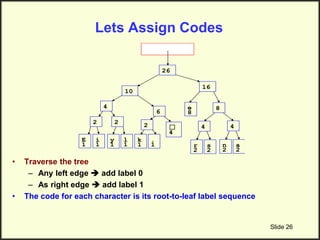
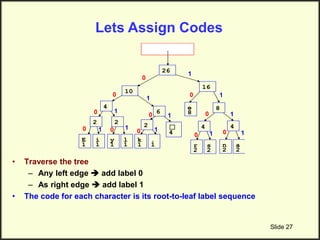
11. Step 2: Build Huffman Tree & Assign Codes
• It is a binary tree in which each character is a leaf node
– Initially each node is a separate root
• At each step
– Select two roots with smallest frequency and connect them to
a new parent (Break ties arbitrary) [The greedy choice]
– The parent will get the sum of frequencies of the two child
nodes
• Repeat until you have one root
Slide 11

12. Example
Slide 12
Char Freq. Char Freq. Char Freq.
E 1 y 1 k 1
e 8 s 2 . 1
r 2 n 2
i 1 a 2
space 4 l 1
E
1
i
1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
Each char. has a
leaf node with its
frequency

13. Find the smallest two frequencies…Replace them
with their parent
Slide 13
E
1
i
1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
E
1
i
1
2

14. Slide 14
E
1
i
1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
2
Find the smallest two frequencies…Replace them
with their parent
y
1
l
1
2

15. Slide 15
E
1
i
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
2
y
1
l
1
2
Find the smallest two frequencies…Replace them
with their parent
k
1
.
1
2

16. Slide 16
E
1
i
1
r
2
s
2
n
2
a
2
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
Find the smallest two frequencies…Replace them
with their parent
r
2
s
2
4

17. Slide 17
E
1
i
1
n
2
a
2
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
Find the smallest two frequencies…Replace them
with their parent
n
2
a
2
4

18. Slide 18
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
Find the smallest two frequencies…Replace them
with their parent
E
1
i
1
2
y
1
l
1
2
4

19. Slide 19
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4 4
Find the smallest two frequencies…Replace them
with their parent
☐
4
k
1
.
1
2
6

20. Slide 20
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4 4 6
Find the smallest two frequencies…Replace them
with their parent
r
2
s
2
4
n
2
a
2
4
8

21. Slide 21
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6 8
Find the smallest two frequencies…Replace them
with their parent
E
1
i
1
☐
4
2
y
1
l
1
2
k
1
.
1
2
4
6
10

22. Slide 22
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4 4
6
8 10
Find the smallest two frequencies…Replace them
with their parent
e
8
r
2
s
2
4
n
2
a
2
4
8
16

23. Slide 23
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6
8
10 16
Find the smallest two frequencies…Replace them
with their parent

24. Slide 24
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6
8
10
16
26
Now we have a single root…This is the Huffman Tree

25. Lets Analyze Huffman Tree
Slide 25
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6
8
10
16
26
• All characters are at the leaf nodes
• The number at the root = # of characters in the file
• High-frequency chars (E.g., “e”) are near the root
• Low-frequency chars are far from the root

26. Lets Assign Codes
• Traverse the tree
– Any left edge  add label 0
– As right edge  add label 1
• The code for each character is its root-to-leaf label sequence
Slide 26
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6
8
10
16
26

27. Slide 27
E
1
i
1
☐
4
e
8
2
y
1
l
1
2
k
1
.
1
2
r
2
s
2
4
n
2
a
2
4
4
6
8
10
16
26
0
1
0
0
0
0
0
0 0
1
1
1
1
1
1
1
1
0
0
0
1 1
• Traverse the tree
– Any left edge  add label 0
– As right edge  add label 1
• The code for each character is its root-to-leaf label sequence
Lets Assign Codes

28. Slide 28
• Traverse the tree
– Any left edge  add label 0
– As right edge  add label 1
• The code for each character is its root-to-leaf label sequence
Lets Assign Codes
Char Code
E 0000
i 0001
y 0010
l 0011
k 0100
. 0101
space☐ 011
e 10
r 1100
s 1101
n 1110
a 1111
Coding Table

29. Huffman Algorithm
• Step 1: Get Frequencies
– Scan the file to be compressed and count the occurrence of
each character
– Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
– Build a Huffman-code tree (binary tree)
– Traverse the tree to assign codes
• Step 3: Encode (Compress)
– Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
– Huffman tree is the key to decompess the file
Slide 29

30. Generate the
encoded file
Step 3: Encode (Compress) The File
Slide 30
Eerie eyes seen near lake.
Input File:
Char Code
E 0000
i 0001
y 0010
l 0011
k 0100
. 0101
space☐ 011
e 10
r 1100
s 1101
n 1110
a 1111
Coding Table
+
000010 1100 000110 ….
Notice that no code is prefix to any other code 
Ensures the decoding will be unique (Unlike Slide 8)

31. Step 4: Decode (Decompress)
• Must have the encoded file + the coding tree
• Scan the encoded file
– For each 0  move left in the tree
– For each 1  move right
– Until reach a leaf node  Emit that character and go back to the root
Slide 31
000010 1100 000110 ….
+
Eerie …
Generate the
original file

32. Huffman Algorithm
• Step 1: Get Frequencies
– Scan the file to be compressed and count the occurrence of
each character
– Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
– Build a Huffman-code tree (binary tree)
– Traverse the tree to assign codes
• Step 3: Encode (Compress)
– Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
– Huffman tree is the key to decompess the file
Slide 32