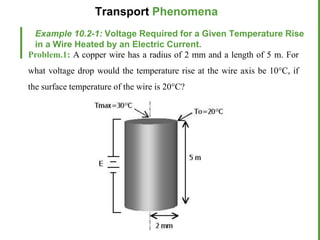
Mujeeb UR Rahman is a chemical engineering student at Mehran University of Engineering & Technology in Pakistan who can be found on SlideShare, ResearchGate, and Academia. The document provides an example of calculating the voltage required to cause a 10°C temperature rise in a copper wire heated by an electric current. It then asks the reader to repeat the analysis assuming the heat flux at the wall is given by Newton's law of cooling using the known heat transfer coefficient and ambient air temperature. The solution proceeds similarly but uses Newton's law of cooling to determine the second integration constant and gives the final temperature profile in terms of the surface temperature and ambient air temperature.

1. 1
Transport Phenomena
Numerical (Shell Energy Balances and
Temperature Distributions in Solids and
Laminar Flow)

2. 2
HELLO!
I’m Mujeeb UR
Rahman
Chemical Engineering student @Mehran
University of Engineering & Technology
Jamshoro, Pakistan.
You can find me at SlideShare
@MujeebURRahman38
ResearchGate @Mujeeb UR Rahman, Academia @Mujeeb UR
Rahman

3. Example 10.2-1: Voltage Required for a Given Temperature Rise
in a Wire Heated by an Electric Current.
Problem.1: A copper wire has a radius of 2 mm and a length of 5 m. For
what voltage drop would the temperature rise at the wire axis be 10°C, if
the surface temperature of the wire is 20°C?
Transport Phenomena

4. 𝑆𝑒 =
𝐼2
𝑘𝑒
(1)
𝑇𝑚𝑎𝑥 − 𝑇𝑜 =
𝑆𝑒𝑅2
4𝑘
(2)
Gives…
𝑇𝑚𝑎𝑥 − 𝑇𝑜 =
𝐼2𝑅2
4𝑘𝑘𝑒
𝐼 = 𝑘𝑒
𝐸
𝐿
Solution:
Transport Phenomena
Combining Eq. 1 and 2
The current density is related to the voltage drop E over a length L by

5. 𝑇𝑚𝑎𝑥 − 𝑇𝑜 =
𝑘𝑒
𝐸
𝐿
2
𝑅2
4𝑘𝑘𝑒
𝑇𝑚𝑎𝑥 − 𝑇𝑜 = 𝑘𝑒
2
𝐸2
𝐿2
𝑅2
4𝑘𝑘𝑒
𝑇𝑚𝑎𝑥 − 𝑇𝑜 =
𝐸2
𝑅2
4𝐿2
𝑘𝑒
𝑘
Transport Phenomena
Hence
From which
𝐸 = 2
𝐿
𝑅
𝑘
𝑘𝑒𝑇𝑜
𝑇𝑜 𝑇𝑚𝑎𝑥 − 𝑇𝑜

6. For copper, the Lorenz number of d§59.5 is k/keTo = 2.23× 10−8𝑣𝑜𝑙𝑡2/𝐾2.
Therefore, the voltage drop needed to cause a 10°C temperature rise is
6
R:=2*mm; L:=5*m;T0:=293*K; Tmax:=T0+10*K; Given data with units
R =2 mm
K = 5 m
To = 293 K
Tmax = 303 K
𝐸 = 2
5000 𝑚𝑚
2 𝑚𝑚
2.23 × 10−8 𝑣𝑜𝑙𝑡/𝐾 293 303 − 293 𝐾
= (5000)(1.49× 10−8)(54.1) = 40 volts
Putting values in Eq.
Transport Phenomena

7. Problem.2: Repeat the analysis in §10.2, assuming that To is not known,
but that instead the heat flux at the wall is given by Newton's "law of
cooling. Assume that the heat transfer coefficient h and the ambient air
temperature Tair are known.
Transport Phenomena
Solution I:
The solution proceeds as before through Eq. 𝑇 = −
𝑆𝑒𝑟2
4𝑘
+ 𝐶2 …(1), but the
second integration constant is determined from Eq. Newton’s Law of
Cooling: 𝑞 = ℎ 𝑇𝑜 − 𝑇𝑎𝑖𝑟 … (2)
𝐵. 𝐶. 2′: 𝑎𝑡 𝑟 = 𝑅, −𝑘
𝑑𝑇
𝑑𝑟
= ℎ 𝑇 − 𝑇𝑎𝑖𝑟 …(3)
Substituting Eq. (1) into Eq. (3) 𝑔𝑖𝑣𝑒𝑠 𝐶2 = 𝑆𝑒𝑅/2ℎ + 𝑆𝑒𝑅2/4𝑘 + 𝑇𝑎𝑖𝑟
and the temperature profile is then

8. From the surface temperature of the wire is found to be 𝑇𝑎𝑖𝑟 +
𝑆𝑒𝑅
2ℎ
.
𝑇 − 𝑇𝑎𝑖𝑟 =
𝑆𝑒𝑅2
4𝑘
1 −
𝑟
𝑅
2
+
𝑆𝑒𝑅
2ℎ
…(4)
Solution II:
Another method makes use of the result obtained previously in
Eq: 𝑇 − 𝑇𝑜 =
𝑆𝑒𝑅2
4𝑘
1 −
𝑟
𝑅
2
…(5). Although To is not known in the present
problem, we can nonetheless use the result. From Eqs. (2) and
Eq. 𝒬 𝑟=𝑅 = 2𝜋𝑅𝐿 ∙ 𝑞𝑟 𝑟=𝑅 = 2𝜋𝑅𝐿 ∙
𝑆𝑒𝑅
2
= 𝜋𝑅2𝐿 ∙ 𝑆𝑒 …(6) we can get the
temperature difference.
Transport Phenomena

9. Subtraction of Eq.7 from Eq.5 enables us to eliminate the unknown To and
gives Eq. 4
𝑇𝑜 − 𝑇𝑎𝑖𝑟 =
𝜋𝑅2𝐿𝑆𝑒
ℎ(2𝜋𝑅𝐿)
=
𝑆𝑒𝑅
2ℎ
… (7)
𝑇 − 𝑇𝑎𝑖𝑟 =
𝑆𝑒𝑅2
4𝑘
1 −
𝑟
𝑅
2
+
𝑆𝑒𝑅
2ℎ
…(4)
Transport Phenomena

10. Thanks!
10
Transport Phenomena