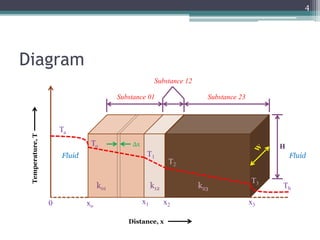
This document discusses heat conduction through composite walls made of layers of different materials. It shows that the resistances to heat transfer of each layer can be combined into a total resistance. Specifically, it: 1) Derives equations for the heat transfer through each individual layer using Fourier's Law. 2) Integrates these equations over the thickness of each layer. 3) Combines the equations and applies boundary conditions at the surfaces to arrive at an expression relating the overall heat transfer to individual layer resistances. 4) Presents the famous formula showing that the overall heat transfer coefficient is equal to the additivity of individual layer resistances.

1. Heat Conduction through
Composite Walls
1

2. Significance
• In industrial heat transfer
problems one is often
concerned with conduction
through walls made up of
layers of various materials,
each with its own
characteristic thermal
conductivity
2

3. Objective
• To show how the various resistances to heat transfer are
combined into a total resistance
3

4. Diagram
Fluid Fluid
Distance, x
Temperature,
T
0 xo
x1 x2 x3
To
T1
T2
T3
Ta
ko1 k12 k23
Δx H
Substance 01
Substance 12
Substance 23
Tb
4

5. Nomenclature
• Three materials of different thicknesses, x1 – xo, x2 – x1, and x3 – x2
• Thermal conductivities k01, k12, and k23
• Ta = Ambient Temperature
• Tb = Fluid Temperature
• The heat transfer at the boundaries x = xo and x = x3, is given by Newton's
"law of cooling" with heat transfer coefficients h0 and h3
5

6. Energy Balance
• For a slab of volume WHΔx:
Heat entering at x = qx|xWH
Heat leaving at x + Δx = qx|x+ Δx WH
6

7. Energy Balance
• For Region 01:
qx|xWH - qx|x+ Δx WH = 0
• Dividing by WHΔx:
• Taking limit Δx→0,
7

8. Integration
• Integrating the previous equation:
• qo = Heat flux at the plane x = xo
• Similarly, for regions 12 and 23:
• With continuity conditions on qx at interfaces, so that the heat flux
is constant and the same for all three slabs
8

9. Applying Fourier’s Law
• Region 01:
• Region 12:
• Region 23:
9

10. Integration over the entire thickness
• We now assume that ko1, k12, and k23, are constants. Then we
integrate each equation over the entire thickness of the relevant slab
of material to get
• Region 01:
• Region 12:
(Eq-1)
(Eq-2)
10

11. Integration over the entire thickness
• Region 23:
• In addition we have the two statements regarding the heat transfer
at the surfaces according to Newton's law of cooling
• At Surface 0:
• At Surface 3:
(Eq-3)
(Eq-4)
(Eq-5)
11

12. Simplification
• Adding Eq-1 through Eq-5
12

13. Final Expression
13

14. General Expression
• Sometimes this result is rewritten in a form reminiscent of Newton's law of
cooling, either in terms of the heat flux qo (J/m2-s) or the heat flow Qo
(J/s):
• The quantity U, called the "overall heat transfer coefficient," is given
then by the following famous formula for the "additivity of resistances“
• Here we have generalized the formula to a system with n slabs of material
14

15. 15