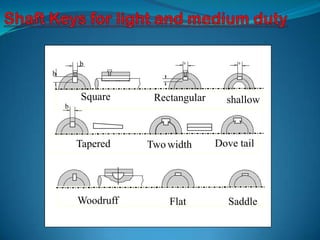
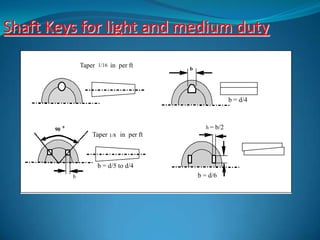
The document discusses different types of shaft keys, how they transmit torque, and their design. It describes various key shapes, sizes, and tapers for different duty levels. Formulas are provided for calculating the crushing strength and shear strength of keys based on the torque transmitted, key dimensions, and material properties. An example problem demonstrates selecting a suitable square key size for a given shaft and torque requirement by analyzing both crushing strength and shear strength.

2.  transmit torque
 keys prevent relative motion,
 Rotary
 axial.
 In some construction they allow
axial motion

3. According to shape
 Straight,
 Tapered,
 Rectangular,
 Square,
 Round,
 Dovetail.
according to their intended duty as:
 Light duty keys
 Medium duty
 Heavy duty

4. b b b
h
Square Rectangular shallow
b
Tapered Two width Dove tail
Woodruff Flat Saddle

5. Shaft Keys for light and medium duty
Taper 1/16 in per ft b
b = d/4
90
0 h= b/2
Taper 1/8 in per ft
b = d/5 to d/4
b b = d/6

6. Pulley shaft assembly
Pressure
distribution

7. Crushing strength:
 The hub is more rigid than the shaft,
The shaft will be twisted , the hub will remain
undistorted.
The pressure along the key will vary
Minimum at the free end
Maximum on the other side.
Maximum pressure : P1
The minimum pressure :P2
h
2
At L the pressure : P.  D
 At Lo the pressure equals 1P
P
to zero P2

L
L2
L0 = 2.25 D
Fig. (5.4)

8. Crushing strength Continue
 The pressure can be expressed by:
 P  P1  L tan  h
2
 Where
 D
( P1  P 2 ) P1 P1
tan    P
L2 L0 P2

L
L2
L 0 = 2 .2 5 D
F ig. (5 .4 )

9. Torque transmitted
 Considering Small length of key (dL)
h
2
dl
 D
P1
P
P2

L
L2
L 0 = 2 .2 5 D
F ig. (5 .4 )
dT  P  dL  1 D
2

10. Integrating between the limits L = 0 to L2
yields: T  1 P DL  1 DL 2 tan 
2 1 2 4 2
The pressure /unit length = b
the crushing stress the area of unit
length, (Sb 0.5h 1) then, h
P1  0 . 5 S b h
Experiments showed that length of key greater than
2.25D is not effective. The pressure at L=2.25D equals zero
and hence, P1 Sbh
tan   
L0 4 .5 D
The torque transmitted can be expressed by,
T  1 S b hDL 2  1 2
4 18
S b hL 2

11. Shear strength
The pressure on the key can be represented by a
diagram
h
2
P 1 = Ss b
where Ss is the
 D
P1
maximum shear at the P
P2
end of the key and

L
hence
L2
P Sb L 0 = 2 .2 5 D
tan   1
 s
L0 2 . 25 D F ig. (5 .4 )
The torque transmitted can be expressed by:
T  S S bDL 2  S S bL
1 1 2
2 9 2

12. Design stages:
 Based on the diameter of the shaft the standard
dimensions of a square can be determined from
table (5.1a) or table (5.1b)
 Solve for crushing strength (Obtain key length)
 It is a second order equation
 L> 2.25 D, rejected
 L< 0 one key is not enough
 L< D then take L = D.
 Check for Shear strength

13. Example:
Find suitable dimensions of a square key to fit
into 3 inch diameter shaft. The shaft transmits
7
16
95 hp at a speed of 200 rpm. The key is made of
steel SAE 1010. Take safety factor of 2.5 and stress
concentration factor k’ = 1.6

14. Solution:
 Torque = Power/ angular speed
 Torque = 63030hp
N
 Torque = 63030 x 95
200
 Torque = 29939 Lb-in
 From table (5.1b), for a shaft with a diameter of inch
7 7
 Key size : x
8 8

15. Crushing strength
 For steel SAE1010: Ss 20000 psi and Se 31000 psi
,(from table 5.2)
 Hence Sb = 2 x 31000 = 62000 psi
 Taking factor of safety = 2.5 and k’ = 1.6
 Sb = 62000/(1.6x2.5) = 15500 psi
 Crushing strength
T  1 S b hDL 
21
4 2 18 S b hL 2
29939  1 15500 x 0 . 875 x 3 . 437 L 2  18 15500 x 0 . 875 L 2
1 2
4
29939  11653.6 L 2  753.5 L 2
2

 L = 3.26 or L = 12.21
 The first root is the answer; the second one
contradicts the condition that L2 < 2.25 D.
therefore the proper length of the key is 3.5

16.  Check for shear from the equation:
T
SS 
L 2 b ( 0 . 5 D  0 . 11 L 2 )
29939
SS 
3 . 5 x 0 . 875 ( 0 . 5 x 3 . 437  0 . 113 . 5 )
 Ss = 7331 psi
 Factor of safety in shear = 20000
 2.73
7331
O.K.

17. Thank You