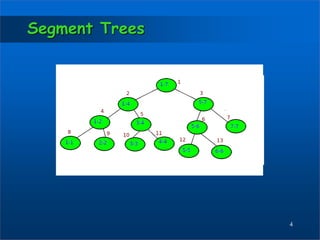
The document discusses segment trees, which allow querying which stored intervals contain a given point. It presents the basic functions of segment trees - initialization, querying, and updating. Initialization builds the tree by dividing segments into halves and storing sums at each node. Querying returns the sum in a range by checking if a segment is fully within, outside of, or partially within the range. Updating modifies values by adding to all relevant nodes. Segment trees enable efficient range minimum/maximum queries and have numerous applications.

1. Segment Tree
1

2. Presented BY:
 Shohanur Rahman
 ID# 1321368042
 CSE 225 (Data Structure)
 North South University
 Email: shohan.nsu.cse@gmail.com
2

3. Segment Tree
Definition:
In computer science, a segment tree is
a tree data structure for storing intervals,
or segments. It allows querying which of
the stored segments contain a given point.
It can be implemented as a
dynamic structure.
3

4. Segment Trees
4

5. Sample Problem:
 You are given n (1<=n<=100000) integers
& 100000 query. Each query you have to
change a value of an element Or you
have to given the minimum value of a
range.
5

6. Function Of segment Tree
6

7. Initial Functions:
We start with a segment arr[1 . . . n].
and every time we divide the current
segment into two halves(if it has not yet
become a segment of length 1), and then
call the same procedure on both halves,
and for each such segment we store the
sum in corresponding node.
7

8. Initial Functions:

9. Initial Functions( in tree look):
9

10. Initial Functions(Algorithm):
#define mx 100001
int arr[mx];
int tree[mx*3];
void init(int node,int b,int e)
{
if(b==e)
{
tree[node]=arr[b];
return;
}
int Left=node*2;
int Right=node*2+1;
int mid=(b+e)/2;
init(Left,b,mid);
init(Right,mid+1,e);
tree[node]=tree[Left]+tree[Right];
} 10

11. Query Functions:
11

12. Query Functions:
 Once the tree is initialized, how to get
the sum using the initialized segment
tree.Now,we use Query function.Here 3
types of cases can be happening.
12

13. Query Functions:
13

14. Query Functions:
case A:
if(b>=i&&e<=j);then the segment is :Releavent
segment.
case B:
if (i > e || j < b);means current segment is
outside of i-j,then its valuless.
case C:
if case A and case B are not true and some of
the parts is included in i-j , then we need to
break the segment and take some of the parts.
14

15. Query Functions(Algorithm):
int query(int node,int b,int e,int i,int j)
{
if (i > e || j < b) return 0;
if (b >= i && e <= j) return tree[node];
int Left=node*2;
int Right=node*2+1;
int mid=(b+e)/2;
int p1=query(Left,b,mid,i,j);
int p2=query(Right,mid+1,e,i,j);
return p1+p2;
}
15

16. Update Function:
 Like tree initialization and query operations,
update can also be done recursively. We are
given an index which needs to update.
Let new value be the value to be added. We
start from root of the segment tree, and
add new value to all nodes which have given
index in their range. If a node doesn’t have
given index in its range, we don’t make any
changes to that node.
16

17. Update Function:
17

18. Update Function(Algorithm):
void update(int node,int b,int e,int i,int newvalue) {
if (i > e || i < b) return;
if (b >= i && e <= i) {
tree[node]=newvalue;
return;
}
int Left=node*2;
int Right=node*2+1;
int mid=(b+e)/2;
update(Left,b,mid,i,newvalue);
update(Right,mid+1,e,i,newvalue);
tree[node]=tree[Left]+tree[Right];
} 18

19. Time Complexity:
Function Name: Time:
1.Initial Function O(n log n)
2.Query Function O(log n)
3.Update Function O(log n)
19

20. Applications:
 Using segment trees we get an <O(N),
O(log N)> algorithm. Segment trees are
very powerful, not only because they can be
used for RMQ(Range Minimum Query). They
are a very flexible data structure, can
solve even the dynamic version of RMQ
problem, and have numerous applications in
range searching problems.
20

21. 21

22. Time to run code……..
22

23. Thank You !
23