The document discusses heap trees, including their definition, representation, operations, and applications. It defines a heap tree as a complete binary tree where the value of each parent node is greater than or equal to its children (for max heaps) or less than or equal (for min heaps). Heap trees can be represented using an array. Common operations are insertion, deletion, and merging. Key applications include sorting algorithms like heapsort and implementing priority queues.

1. Heap tree
in
Data structure By,
Janani.J
I.Msc IT
V.V.Vannaiperumal college for women,

2. Objectives…
╸ Heap tree Definition
╸ Max heap tree
╸ Min heap tree
╸ Representation of a heap tree
╸ Operations of a heap tree
╸ Application of heap tree
2

3. 1.Heap tree
Definition…..

4. HEAP TREE
Definition
A Heap is a complete binary tree.
Suppose H is a complete binary tree.It will be termed heap
tree if it satisfies the following properties:
For each node N in H,the value at N is
greater than or equal to the value of each of the children of N
Or, in other words,N has a value which is
greater than or equal to the value of every successor of N.
There are two types of the heap:
Min Heap
Max heap
4

5. 5
TABLET
PROJECT
Show and explain your web,
app or software projects
using these gadget
templates.

6. 2.Max heap tree

7. 7
Max heap tree
╸ The value of the parent node
should be greater than or equal to
either of its children.
╸ Or
╸ In other words, the max heap can
be defined as for every node I; the
value of node I is less than or
equal to its parent value except
the root node. Mathematically, it
can be defined as:
A[Parent(i)] >= A[i]

8. 3.Min heap tree…

9. 9
Min heap tree
╸ The value of the parent node
should be less than or equal to
either of its children.
╸ Or
╸ In other words, the min-heap can
be defined as, for every node I, the
value of node I is greater than or
equal to its parent value except
the root node. Mathematically, it
can be defined as
A[Parent(i)] <= A[i]

10. 4.Represtation of
a heap tree…

11. Representative of a heap tree
11
╸ A binary heap is typically represented as array. The
representation is done as:
The root element will be at A[0].
Below table shows indexes of other nodes for the ith node,
i.e., A[i]:
A[(i-1)/2] Returns the parent node
A[(2*i)+1] Returns the left child node
A[(2*i)+2] Returns the right child node
The traversal method use to achieve Array representation is
Level Order

12. 5.Operations of a
heap tree….

13. Insertion
Merging
Deletion
13
The major operation required to be
performed on a heap tree are:

14. Insertion of a heap tree
14
╸ Insertion into a heap must maintain both the
complete binary tree structure and the heap order
property.
╸ Its value is compared with its parent’s value,and to
be a Max heap, parent’s value > child’s value is
satisfied, hence the interchange as well as any
further comparison are not required.
╸ Thiis can continue between two nodes on paths
from the newly inserted node to the root node till
We get a parent whose value is greater than its
child or we reach till the root.

15. Algorithm InsertMaxHeap
Input: ITEM, the data to be interested; the strength of node
Output:ITEM,is inserted into the heap tree.
Data structure: Array A[1……SIZE] storage the heap tree;N being t
the tree.
Steps:
1. If(N≥SIZE)then
2. Print”Heap tree is saturated: Insertion is void”
3. Exit
4. Else
5. N=N+1
6. A[N]=ITEM
7. i=N
8. p=I div 2.
9. While (p>0)and(A[p]<A[I]) do
10. temp=A[I] 15

16. 11. A[I]=A[p]
12. A[p]=temp
13. I=p
14. p=p div 2
15. EndWhile
16.EndIf
17.Stop
16

17. 17
Deletion of a heap tree
The principle can be stated as follows:
• Read the root node into a temporary storage
say,ITEM.
• Replace the root node by the last node in
the heap tree.Then reheap the as stated
below:
• Let the newly modifier root node be the
current node.Compare Its value with the value
of its two children.
• Continue reheap if the current node is not an
empty node.

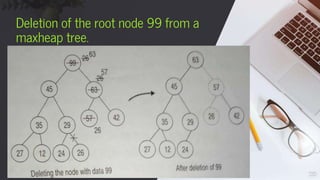
18. Algorithm DeleteMaxHeap
Input: A heap tree with elements.
Output:ITEM,is being the data deleted and the remaining tree after de
Data structure: Array A[1……SIZE] storage the heap tree;N is the numb
Steps:
1. If(N=0)then
2. Print”Heap tree is exhausted:Deletion is not possible”
3. Exit
4. Endif
5. ITEM=A[1]
6. A[1]=A[N]
7. N=N-1
8. Flag=FALSE,I=1
9. While (flag=FALSE)and(i<N) do
10. lchild=2*I,rchild=2*I+1
11. . If(lchild≤N)then
12. x=A[lchilld]
13. Else
18

19. Algorithm DeleteMaxHeap
16. If(rchild≤N)then
17. x=A[rchilld]
18. Else
19. x=-∞
20. EndIf
21. If(A[I]>x) and (A[I]>y) then
22.. Flag=TRUE
23.. Else
24. If(x>y)and (A[i]>x)
25. Swap(A[I],A[lchild])
26. I=lchild
27.. Else
. If(y>x)and (A[i]>y)
Swap(A[I],A[rchild])
I=rchild
28.. EndIf
29.. EndIf
30.. EndIf
31.. EndWhile
32.Stop
19

20. Deletion of the root node 99 from a
maxheap tree.
20
Vestibulum nec congue
tempus
02
03
01

21. Merging two heap trees
The merging operation consists of two steps:
Continue steps 1 and 2 while H2 is not empty
1. Delete the root node,say x,from H2.
2.Insert the node x into H1 satisfying the
property of H1.
21

22. 6.Application of
heap tree….

23. There are two main application of heap trees:
Sorting
Priority queue implementation
Sorting using a heap trees
This actually consists of the following steps:
Step1: Build a heap tree with the given set of data.
Step 2: Delete the root node from the heap.
Rebuild the heap after the deletion.
Place the deleted node in the output
Step 3: Continue step2 until the heap tree is empty.
Application of heap trees
23

24. IN TWO OR THREE COLUMNS
Yellow
Is the color of gold,
butter and ripe
lemons. In the
spectrum of visible
light, yellow is
found between
green and orange.
Blue
Is the colour of the
clear sky and the
deep sea. It is
located between
violet and green on
the optical
spectrum.
Red
Is the color of
blood, and because
of this it has
historically been
associated with
sacrifice, danger
and courage.
24

25. AND TABLES TO COMPARE DATA
A B C
Yellow 10 20 7
Blue 30 15 10
Orange 5 24 16
25

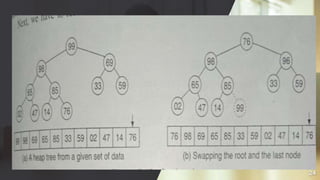
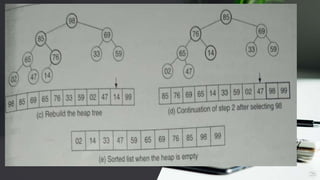
26. Algorithm HeapSort
Input: A set of N input data.
Output: sorted data in ascending order.
Data structure: An Array A where the data will be stored.
Steps:
1. BuildMaxHeap(A)
2. I=N
3. While (I>1) do
4. swap(A[1],A[I])
5. i=i-1
6. j=1
7. While (j<I)do
8. lchild=2*j
9. rchilld=2*j+1
10. If(A[j]<A[lchild]) and (A[lchild]>A[rchilld]) then
11. Swap(A[j],A[lchild])
12. j=lchild
26

27. Algorithm HeapSort
13.. Else
14. If(A[j]<A[rchild]) and (A[rchild]>A[lchilld]) th
15. Swap(A[j],A[rchild])
j=rchild
16.. Else
17. Break ();
18. EndIf
19. EndIf
20. EndWhile
21.EndWhile
22.Stop
27

28. Priority queue implementation using
a heap tree
╸ Priority queue can be implemented using a circular
array,a linkedlist, etc.
╸ Another simplified implementation is possible using a
heap tree; the heap, however, can be represented
using an array.
╸ This implementation is therefore free from the
complexities of the circular array and the linked list
but get advantage of simplicity of the array.
28

29. THANK
you…
:
29