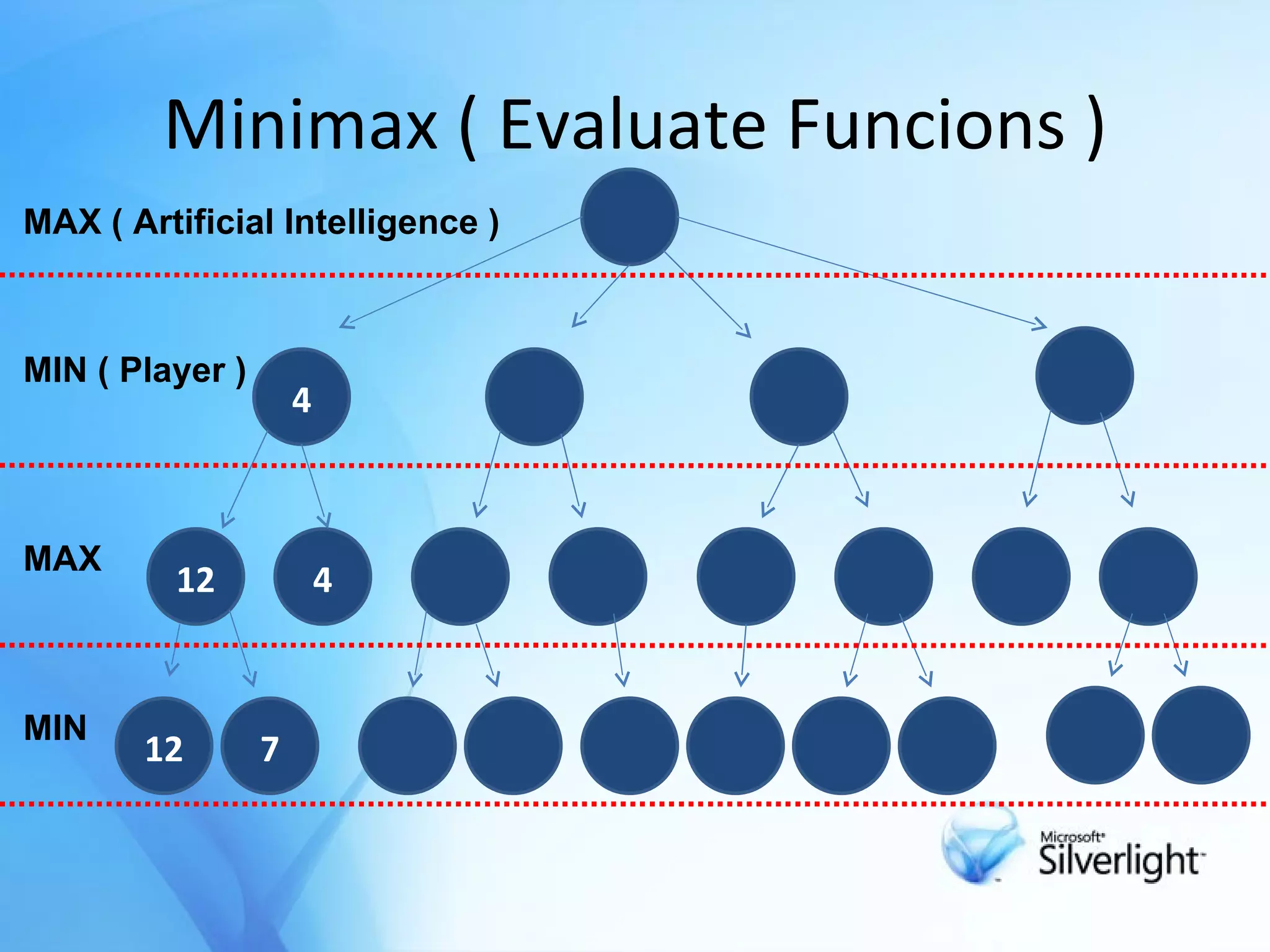
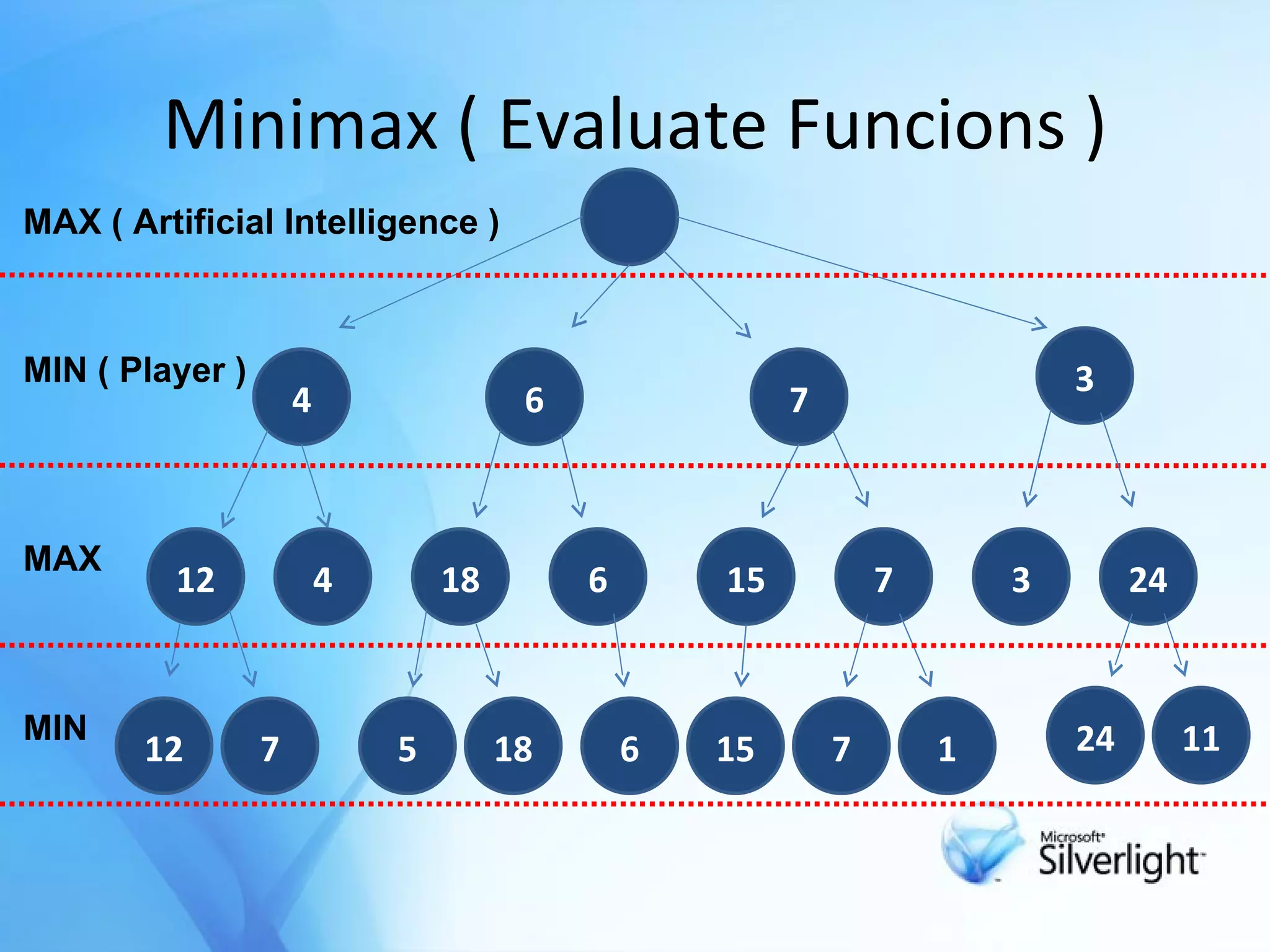
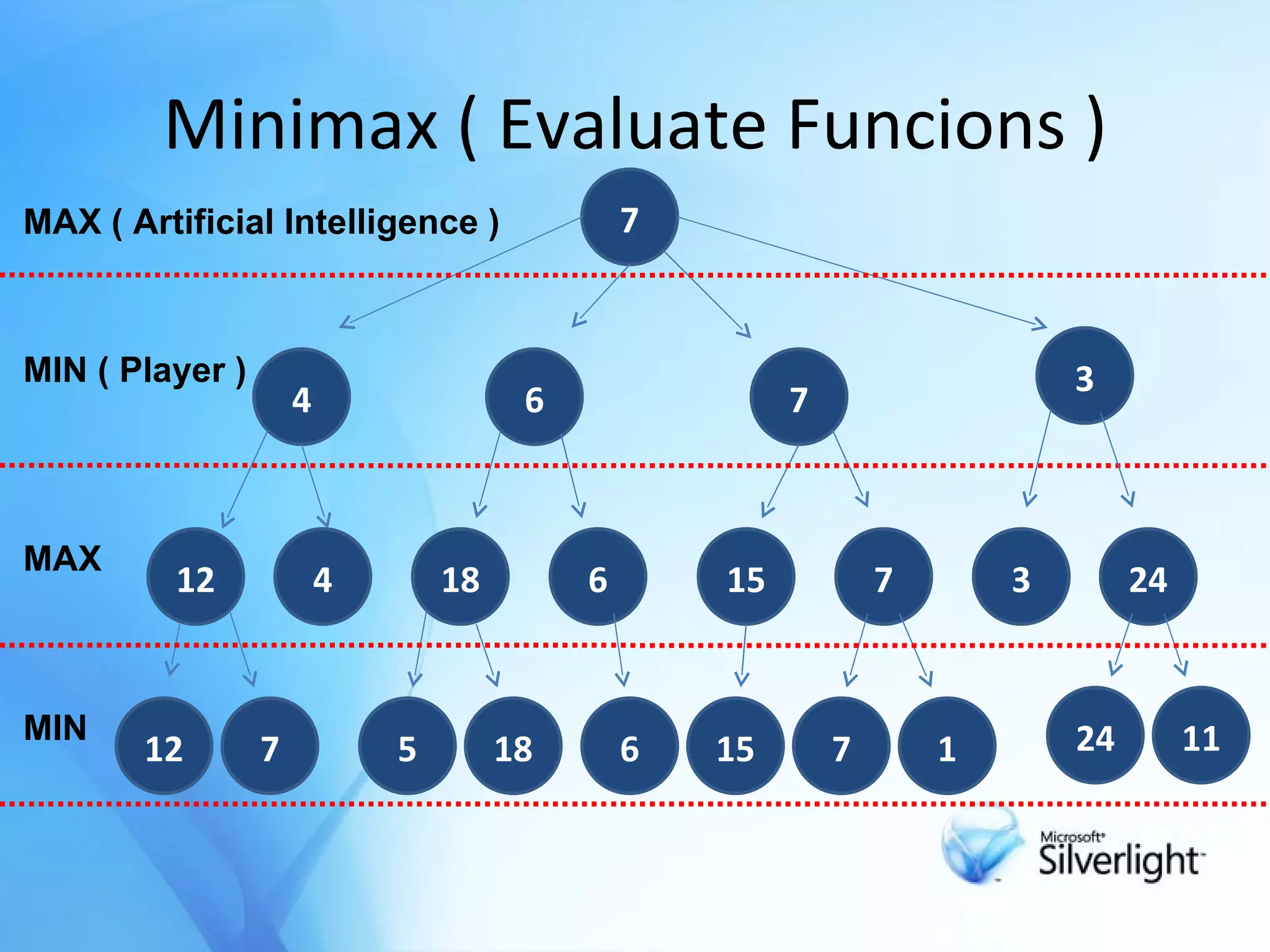
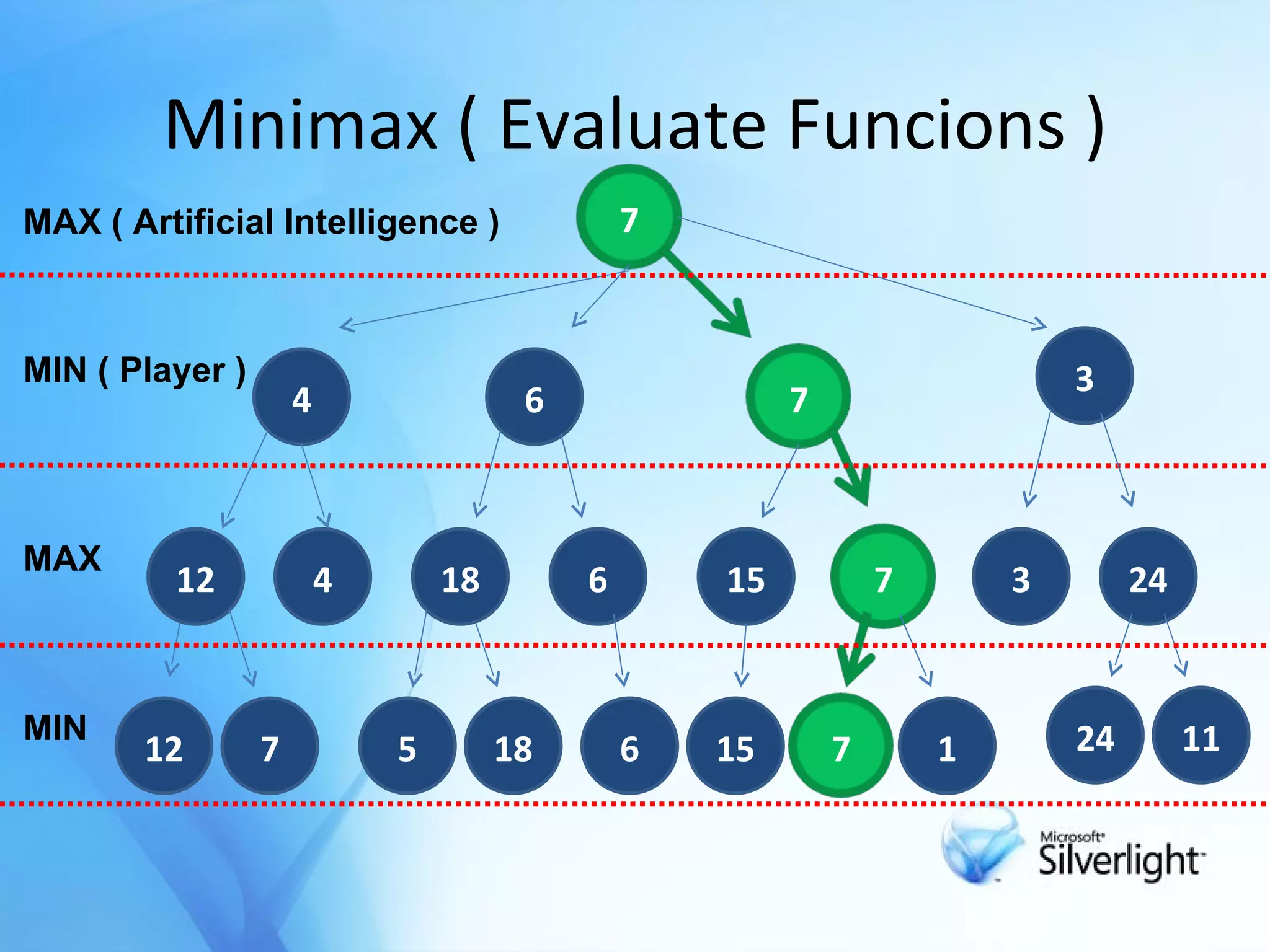
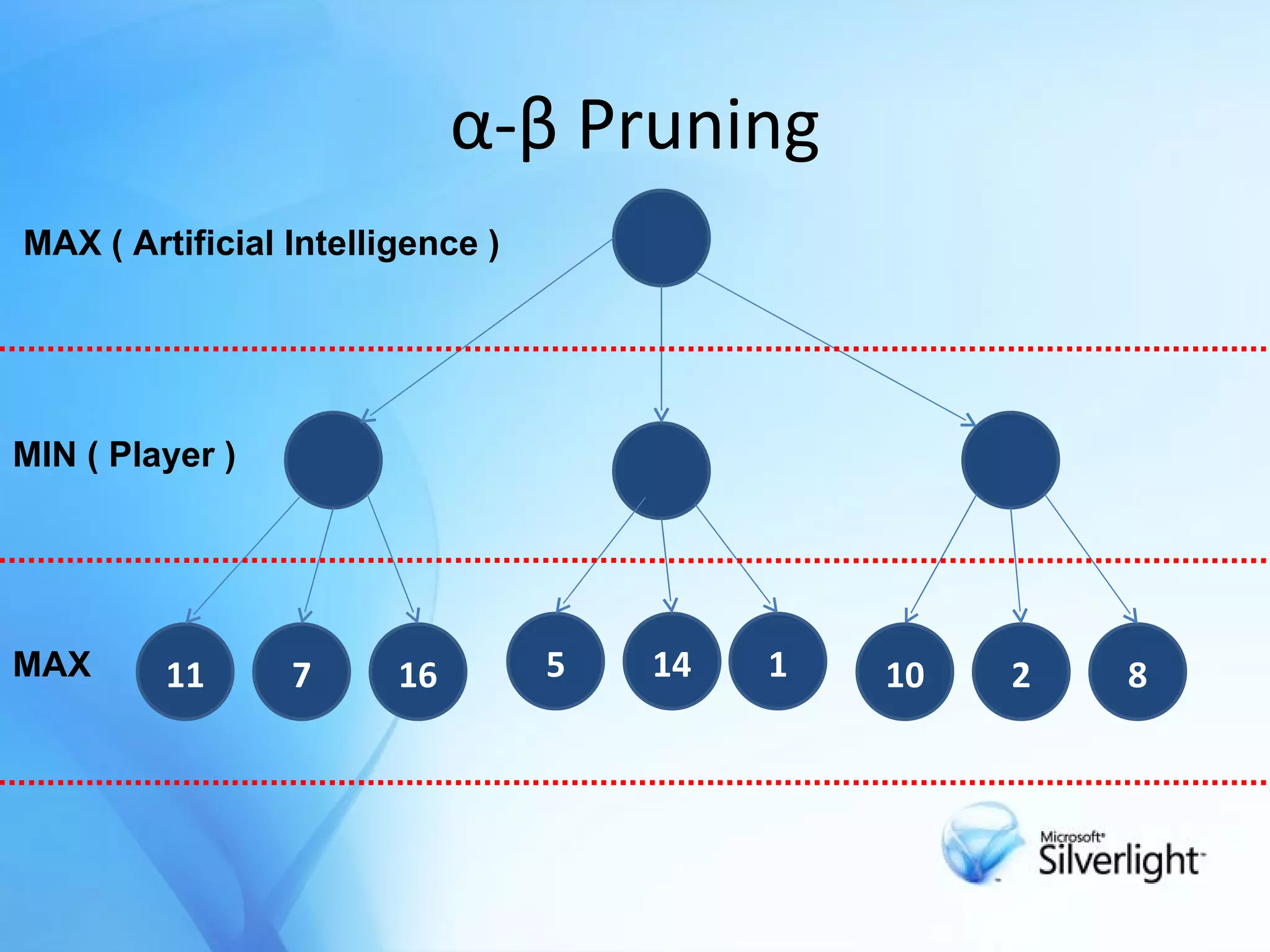
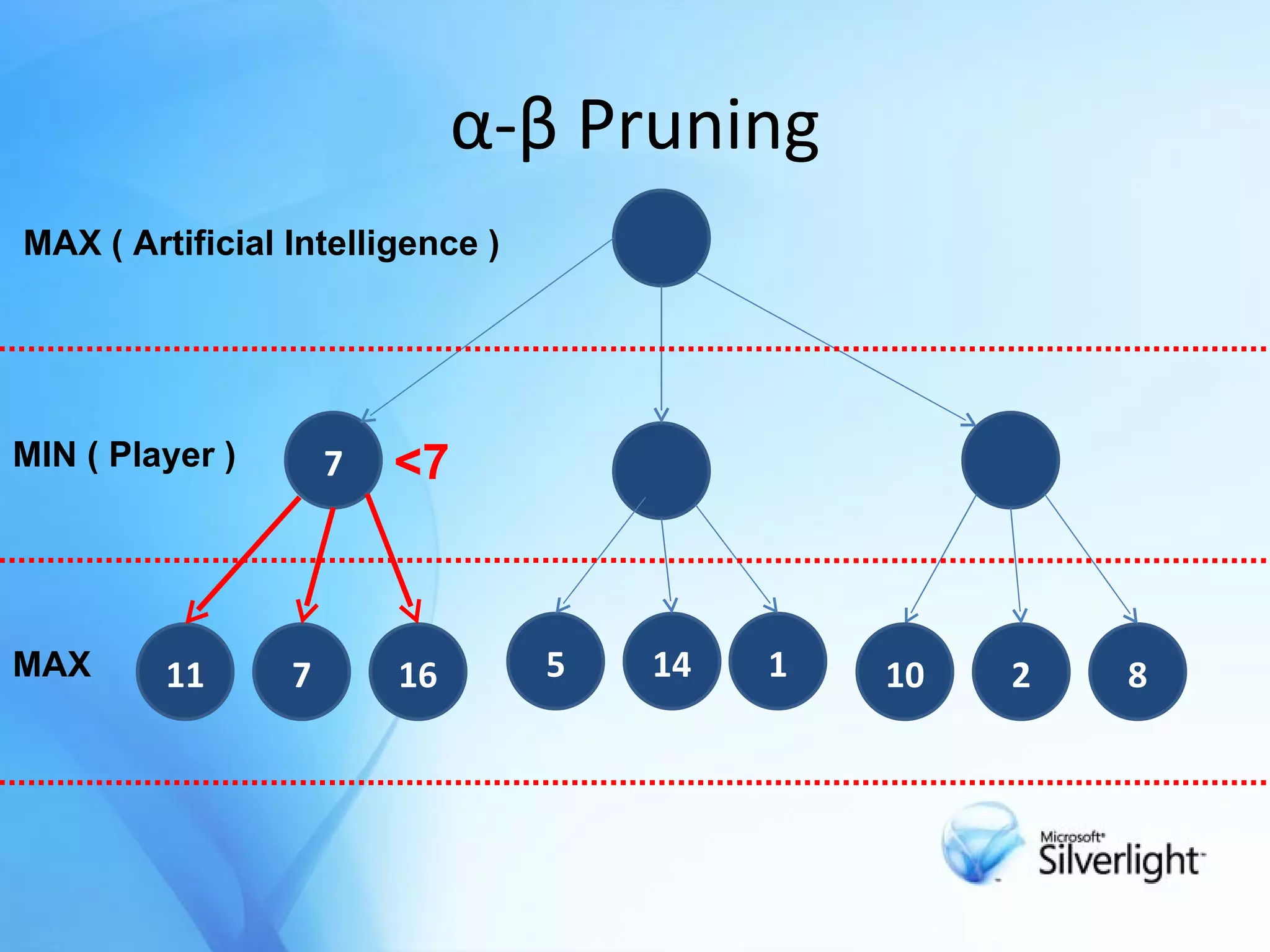
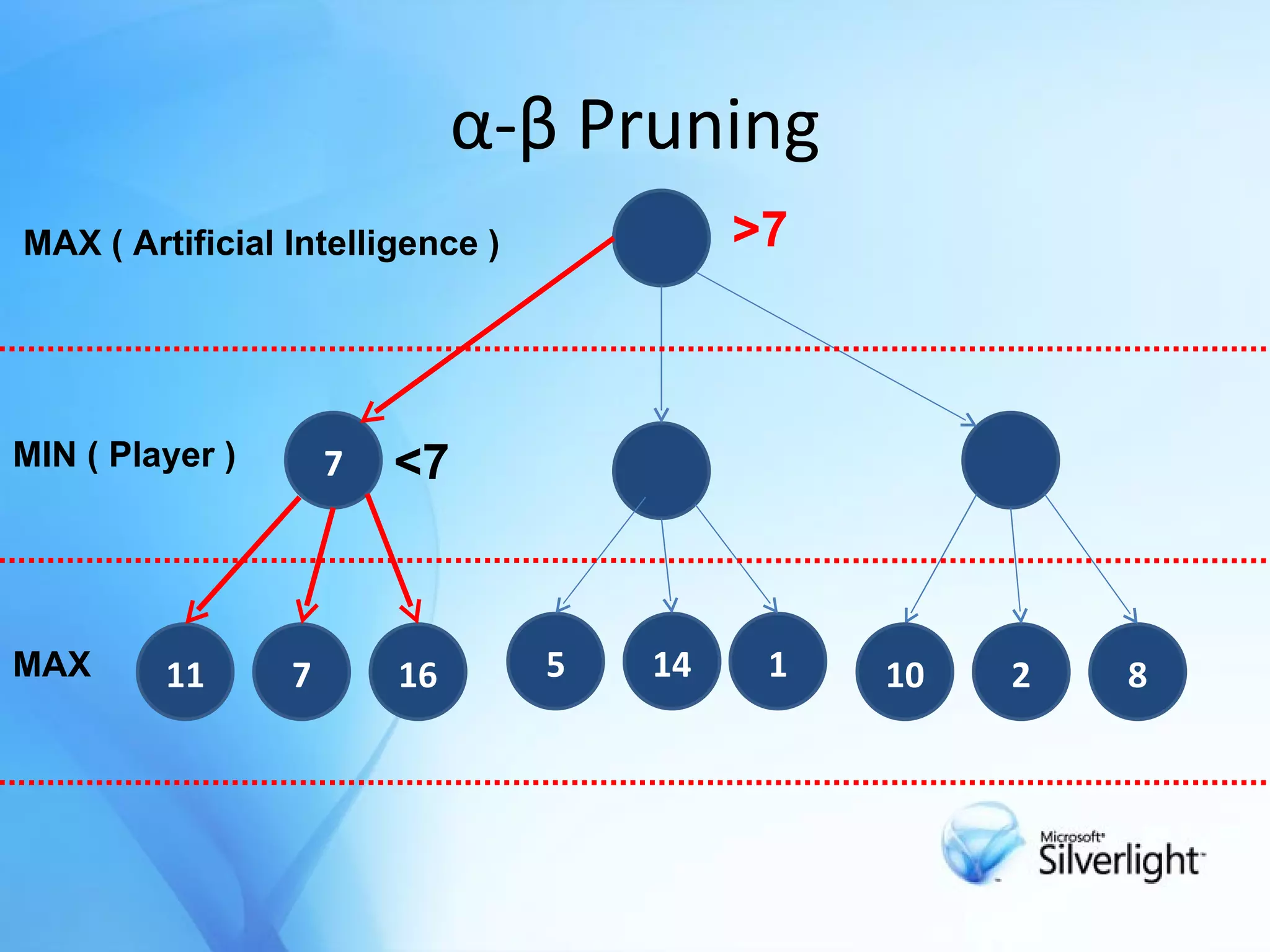
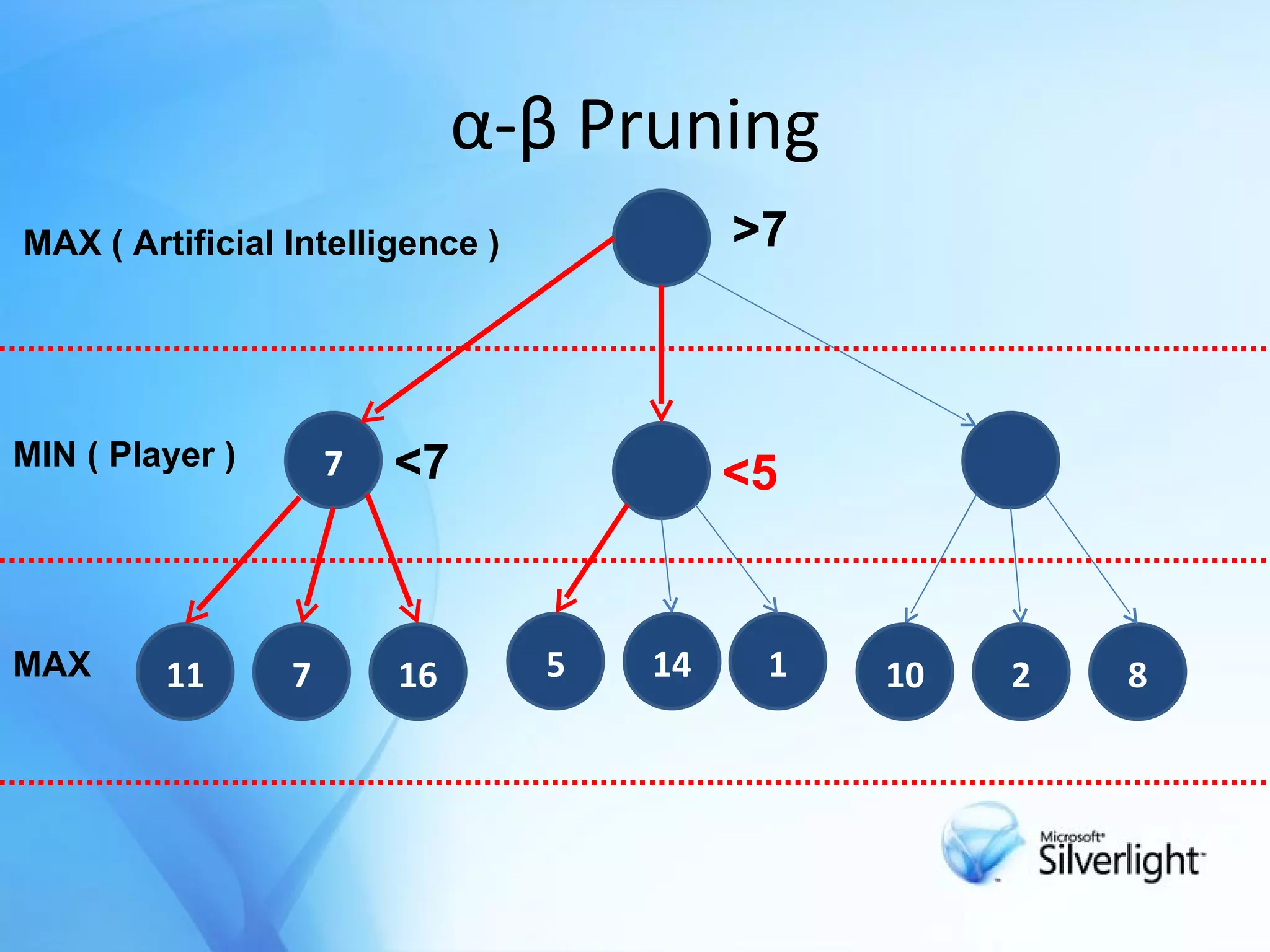
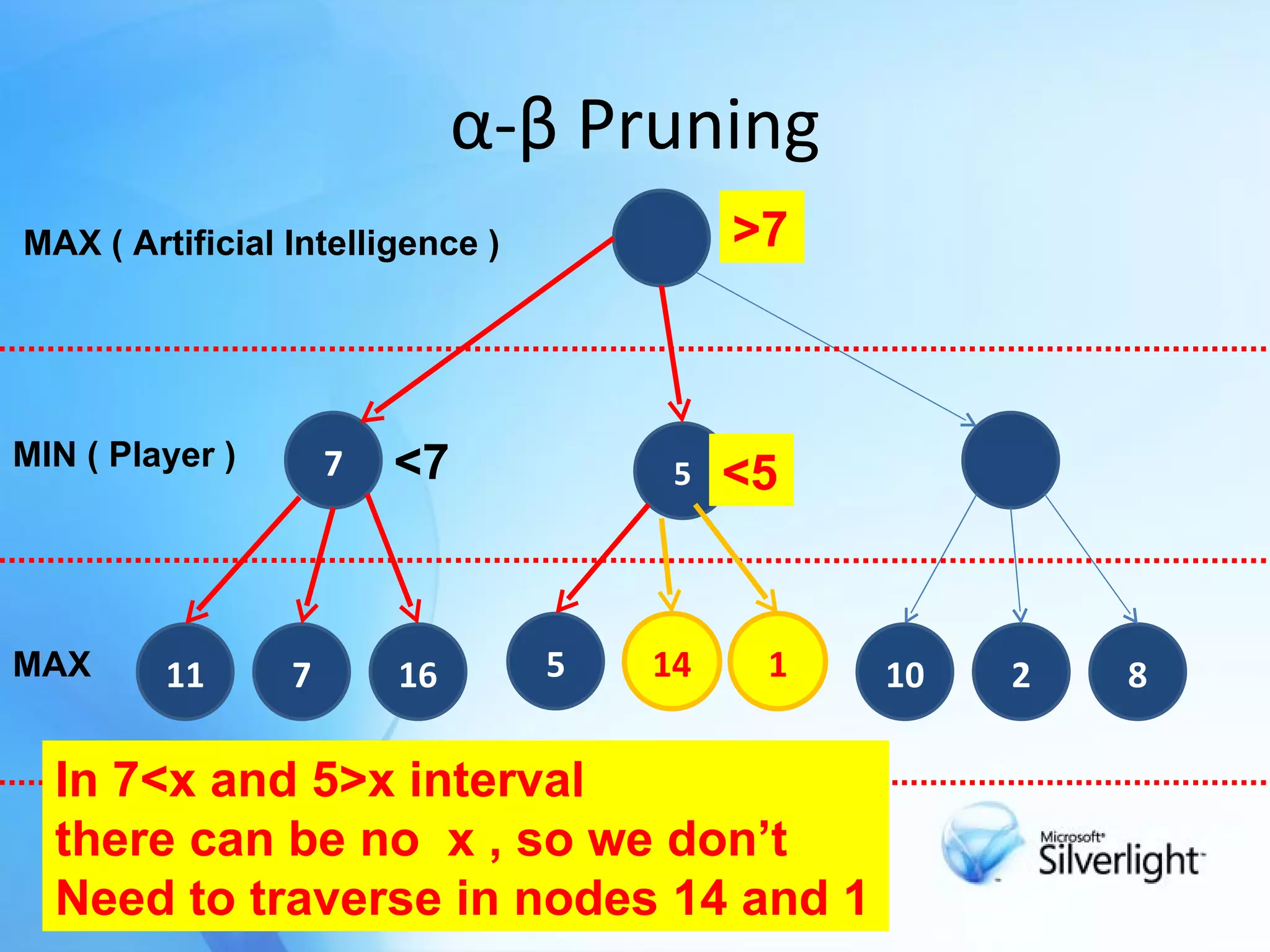
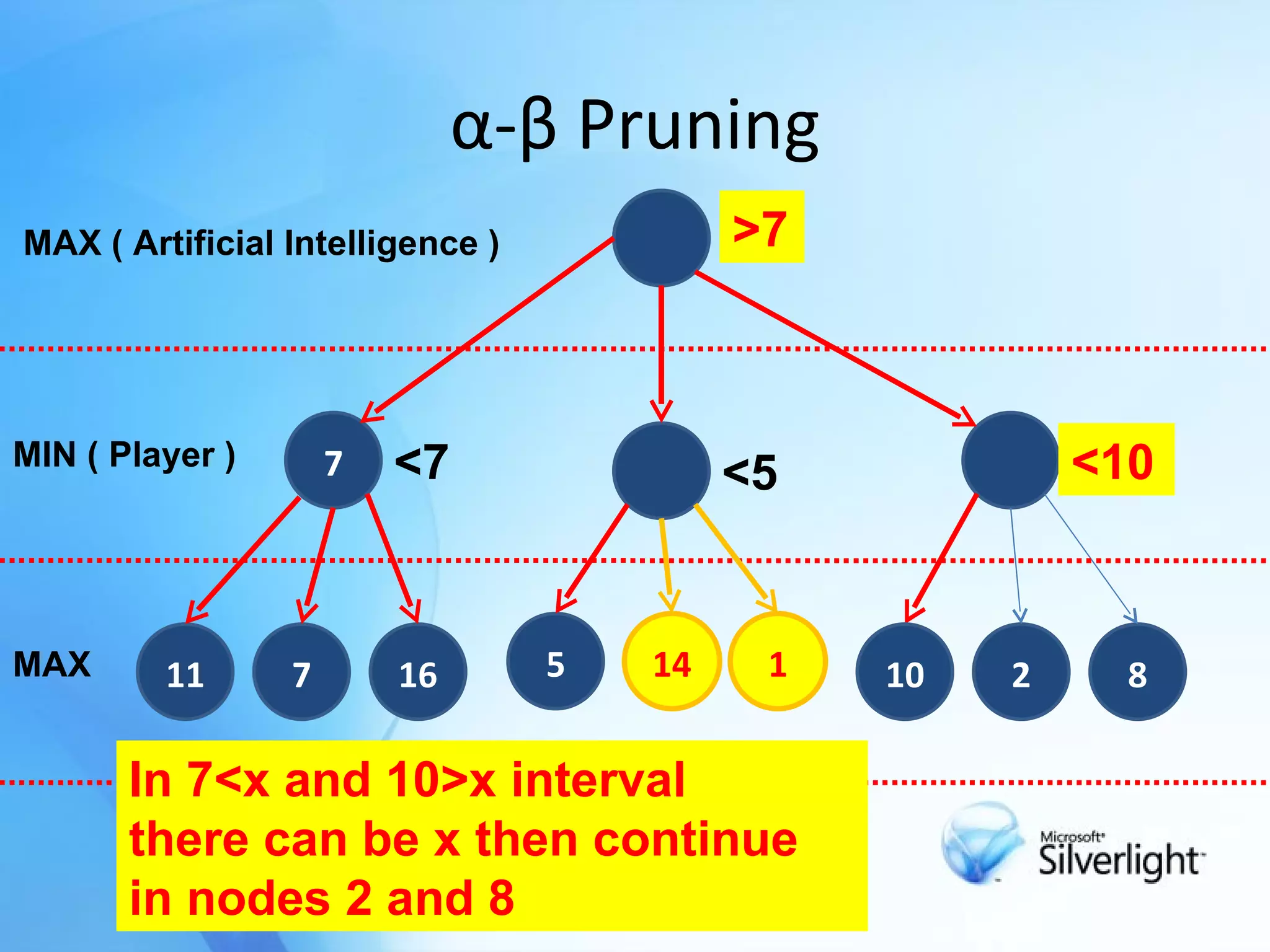
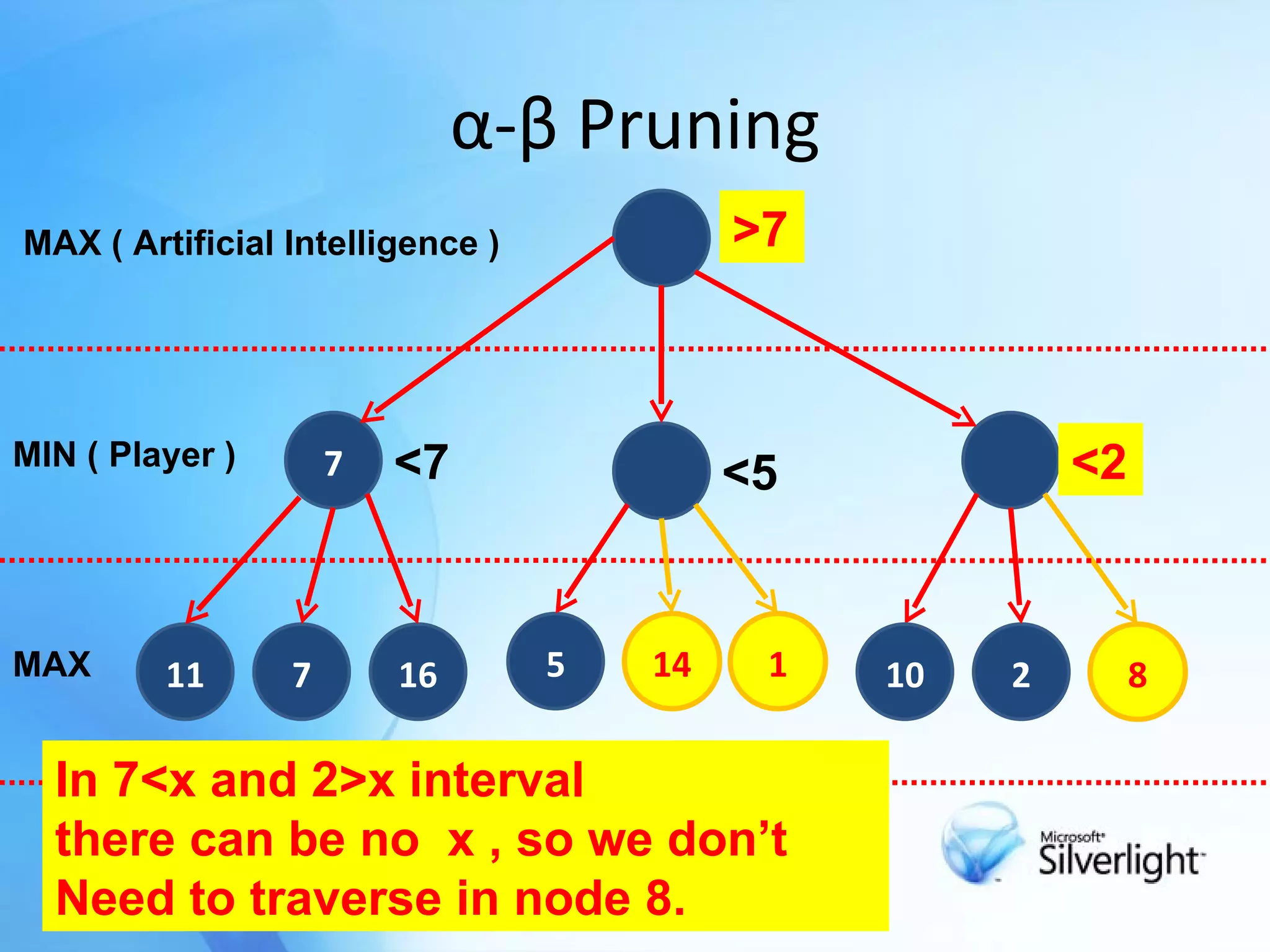
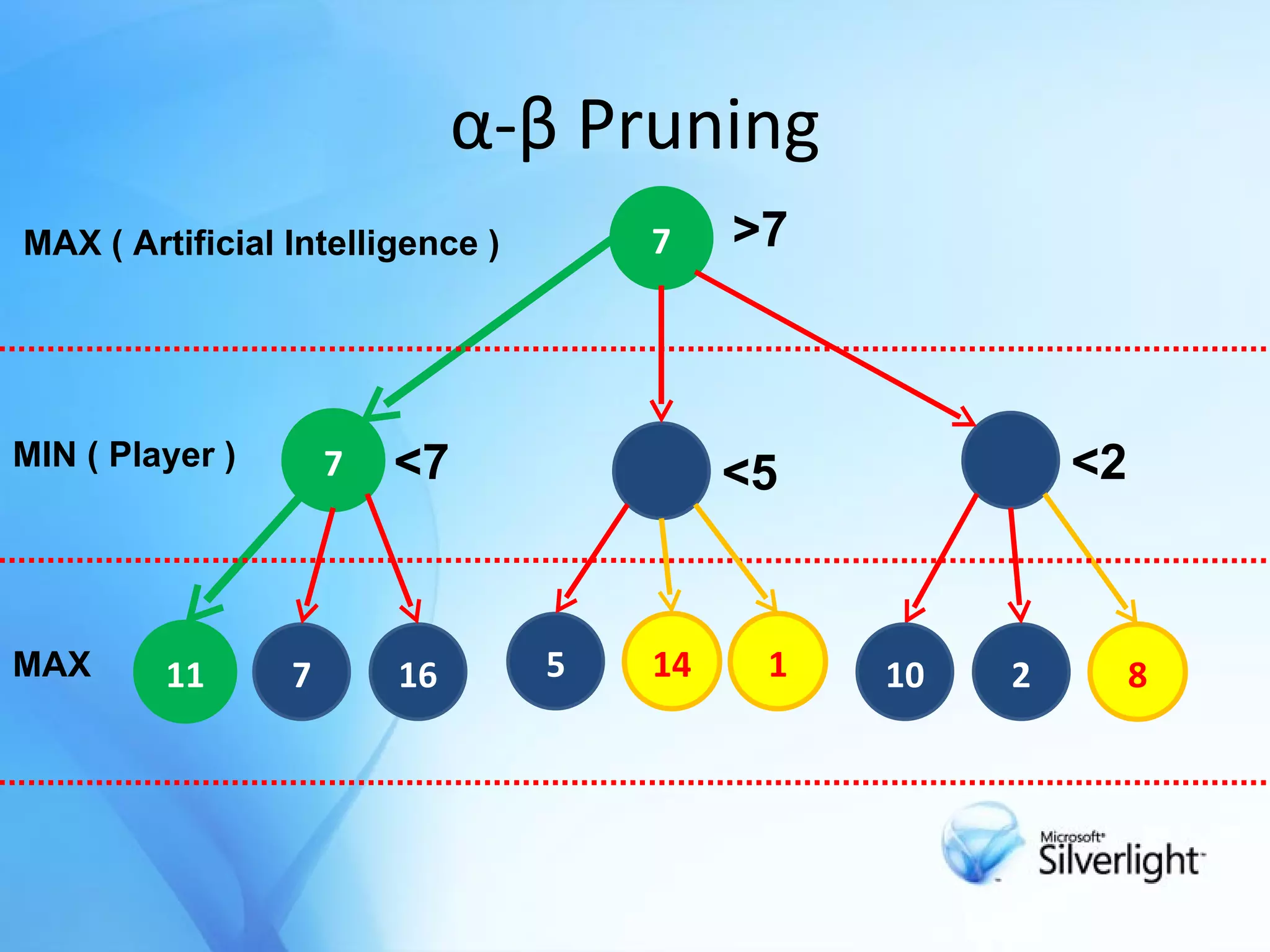
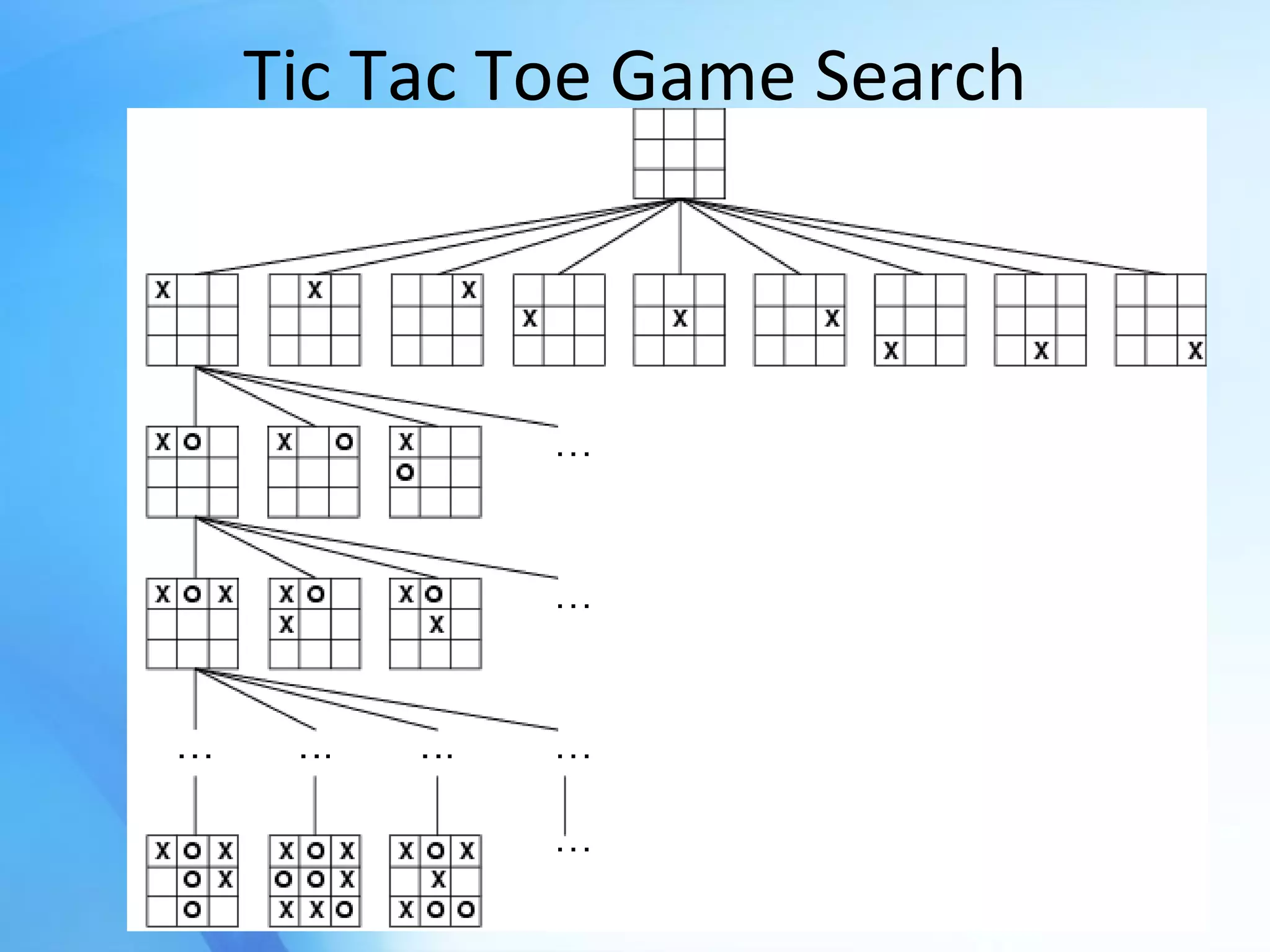
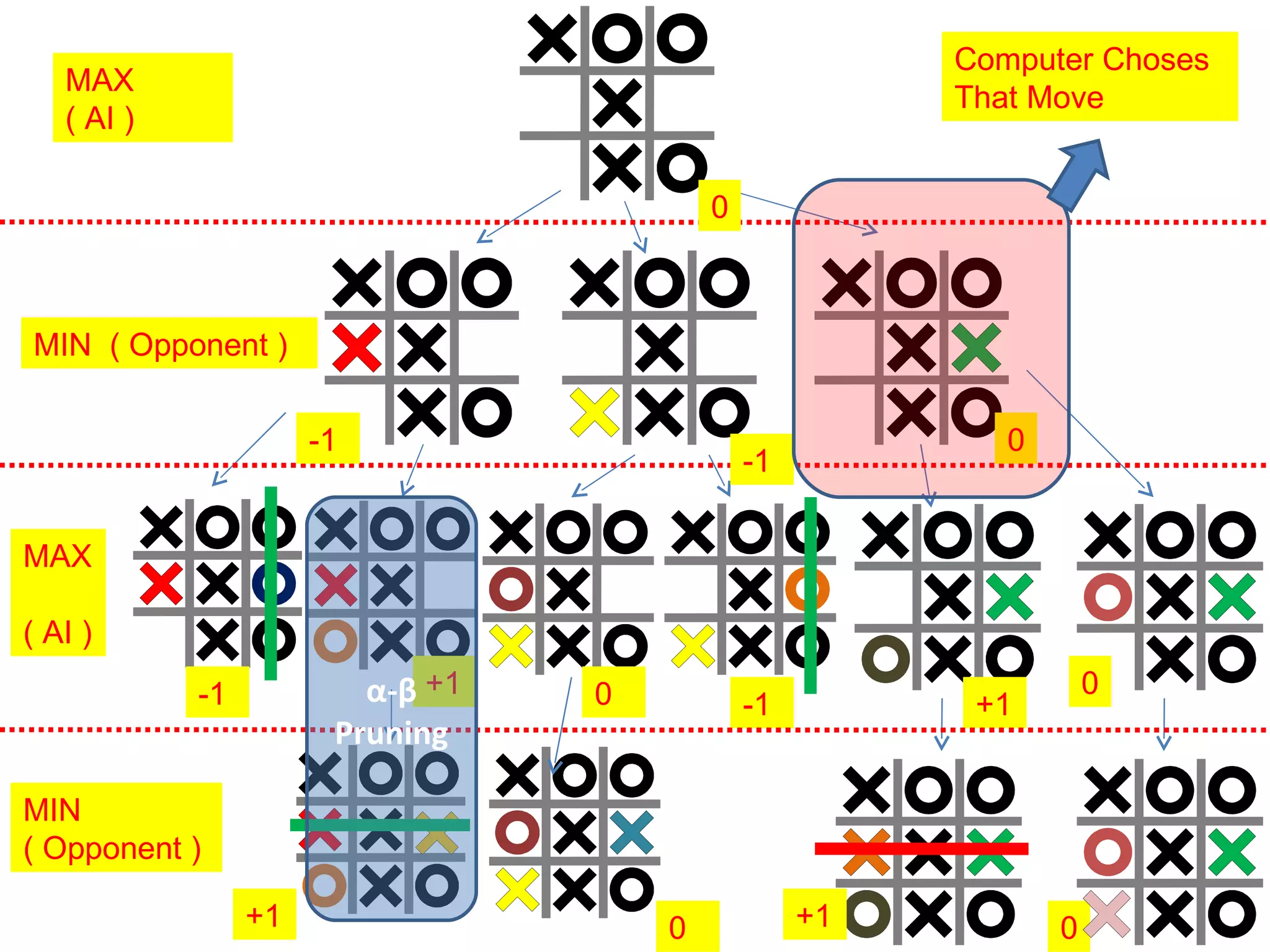
The document discusses the application of artificial intelligence in game playing, particularly focusing on the minimax algorithm and its extension, α-β pruning, for optimizing decision-making in games like Tic Tac Toe. It explains the structure of game trees, the process of generating these trees, evaluating game states, and how α-β pruning reduces the search space to enhance performance. Ultimately, it highlights the role of these techniques in determining the best moves and ensuring optimal gameplay against an opponent.

1. Unbeatable TicTacToe (xox) Alp Çoker www.alpcoker.com [email_address] Game Tree

2. Game playing was one of the first tasks undertaken in AI as soon as computers became programmable.

3. Game Systems Rely On Search techniques Heuristic functions Bounding and pruning techn i qiues Knowledge database on game

4. Board Games Tic Tac Toe,Chess,Go....

5. Why Board Games? T wo opponents . Game states are easy to represent. N ot involving chance or hidden . Search concentrate on one player.

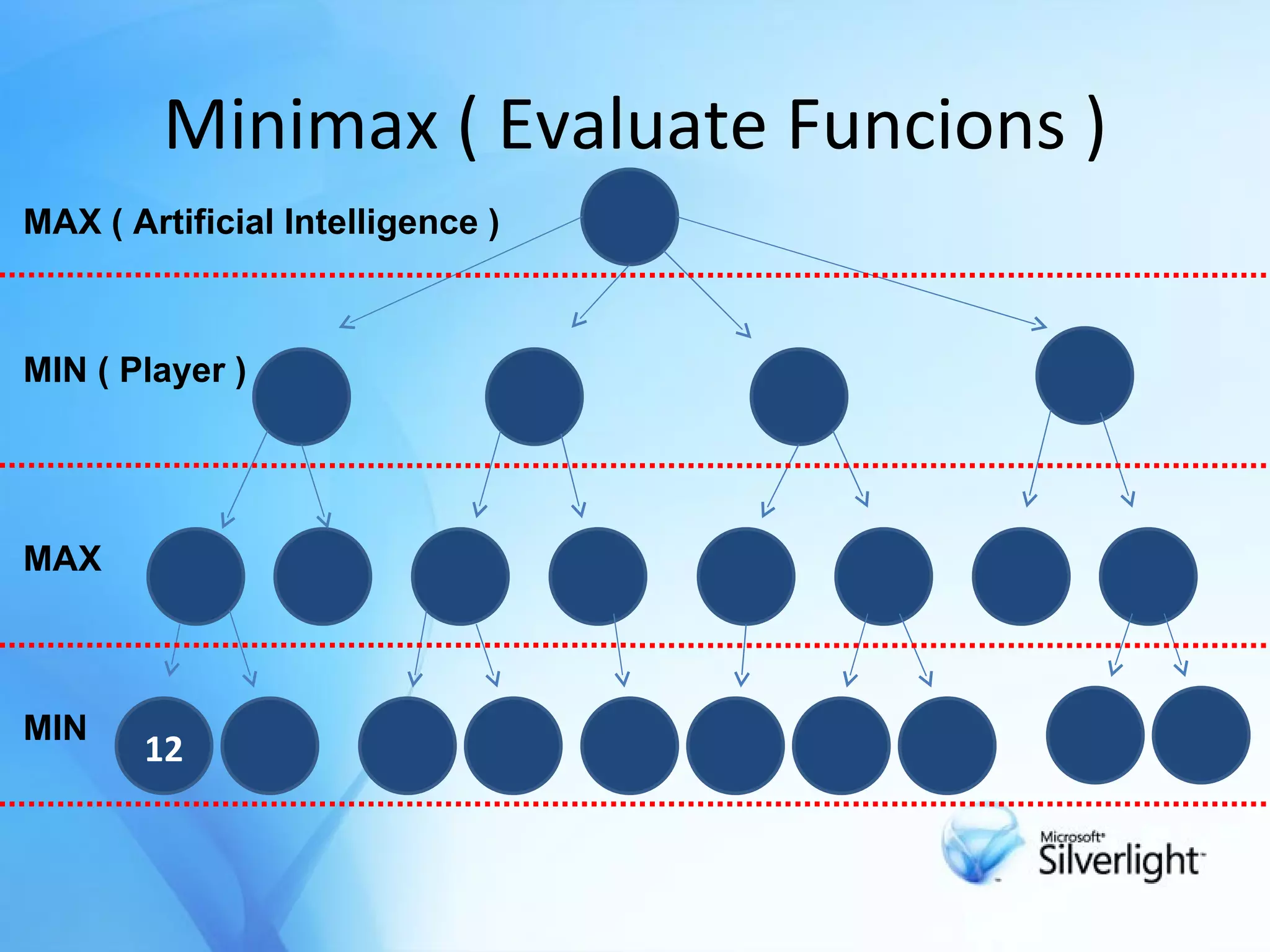
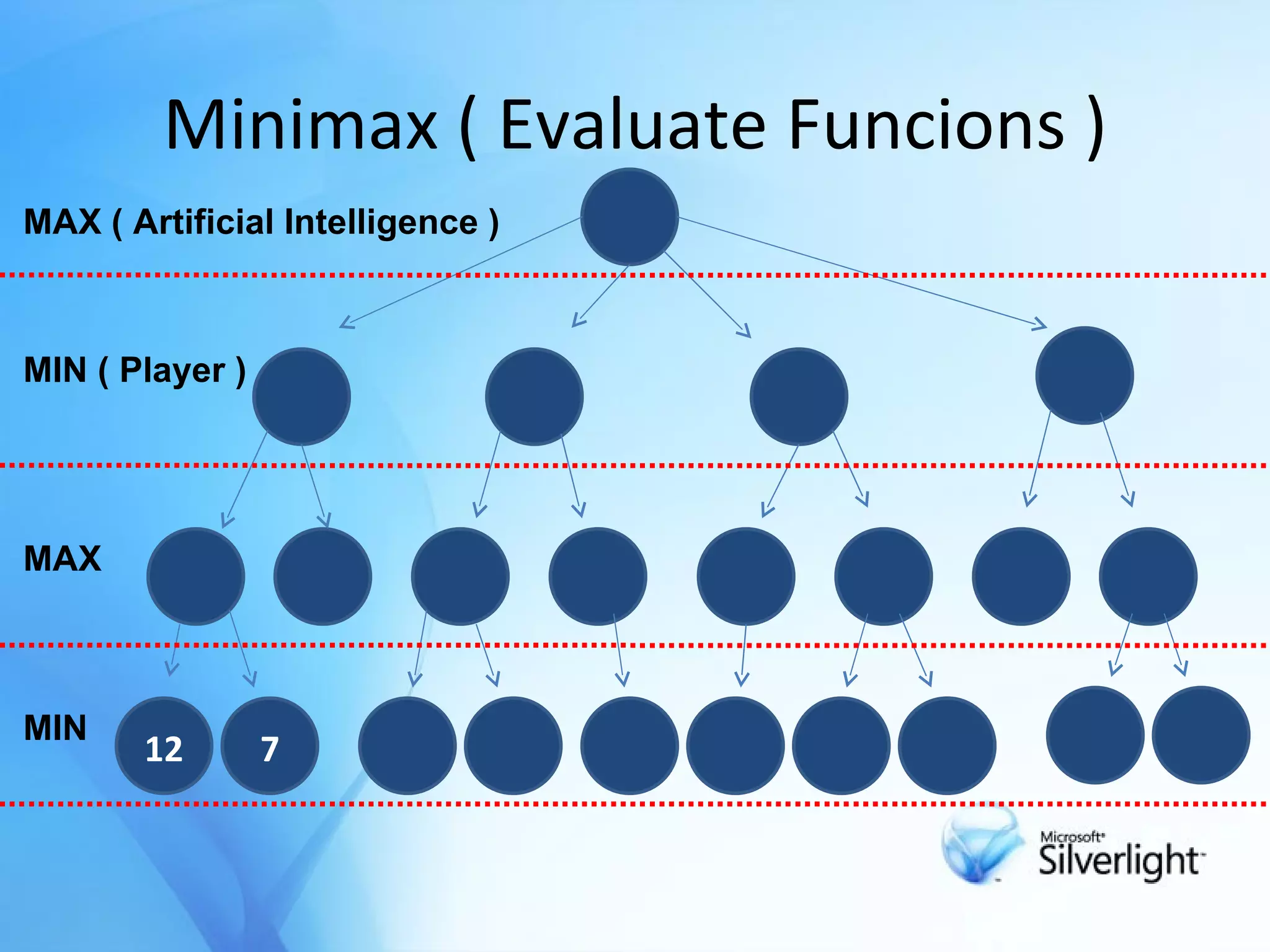
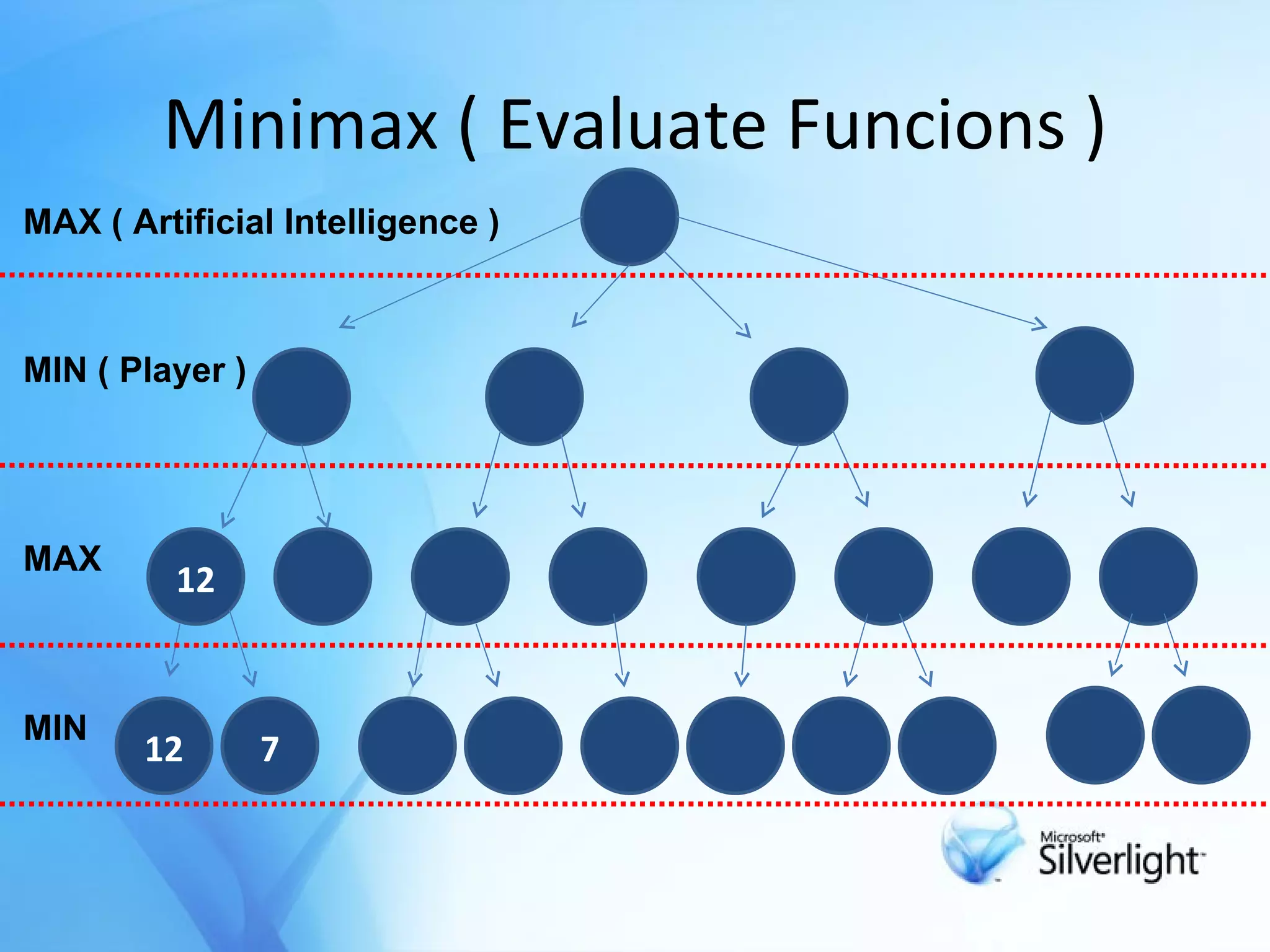
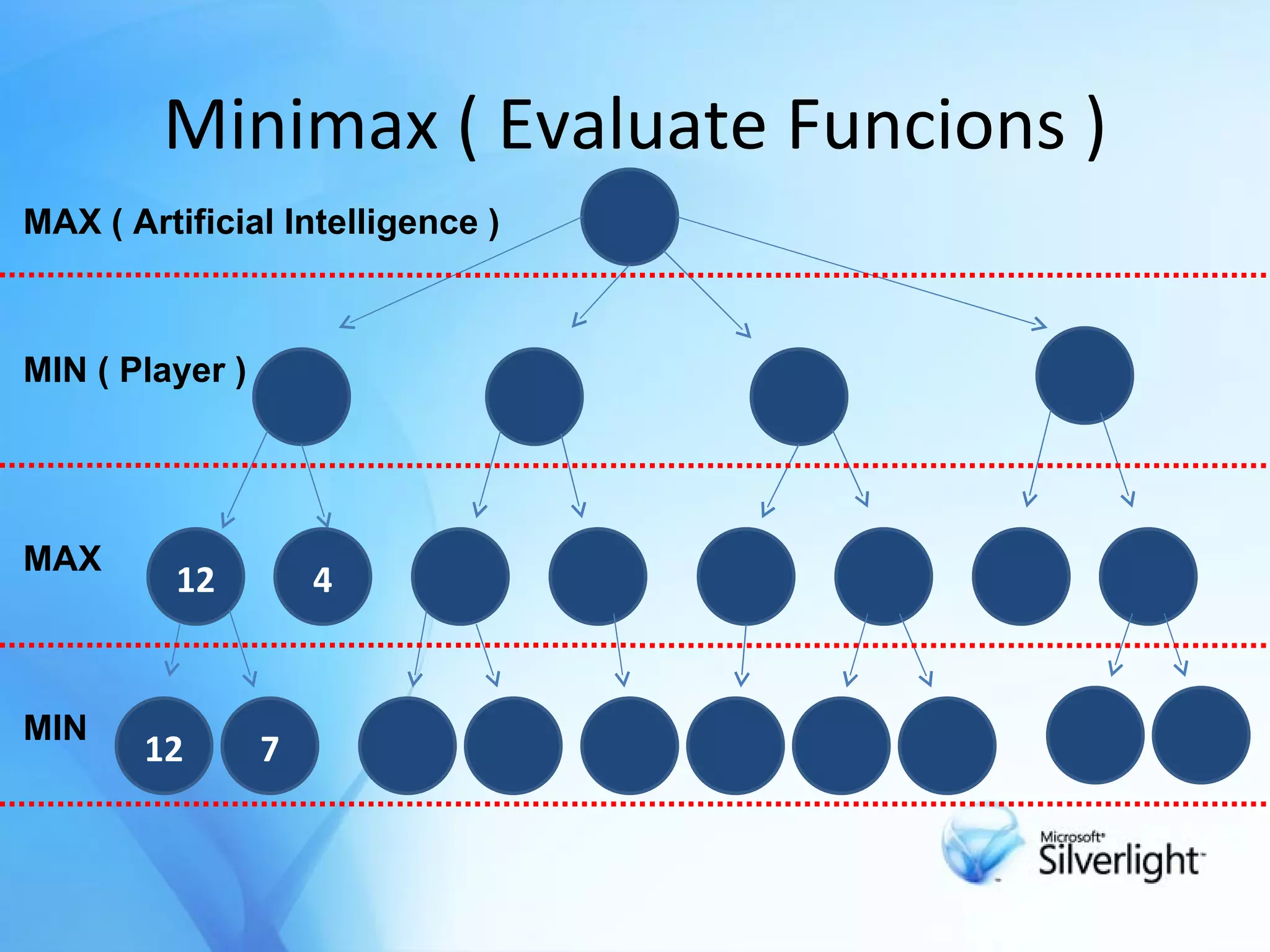
6. Minimax Method Try to find next best move in a game with 2 player . The object of a search is to find a path from the starting position to a goal position It calculates all possible game states by examining all opposing moves . Determine the next move against best play[opponent] .

7. Minimax Method Max tries to maximize its score Min tries to minimize Max’s score (Min) Goal: Move to position of highest minimax value

8. Minimax Method Minimize M aximum L oss OR M aximize M inimum G ain

9. Minimax Search Algorithm 1. Generate the whole game tree to leaves 2. Apply utility (payoff) function to leaves 3. Back-up values from leaves toward the root: * a Max node computes the max of its child values * a Min node computes the Min of its child values 4. When value reaches the root: choose max value and the corresponding move.

10. Evaluation Function Each game outcome has a payoff, which we can represent as a number By convention, we prefer positive numbers In some games, the outcome is either a simple win ( +1 ) or a simple loss ( -1 ) In some games, you might also tie, or draw ( 0 )

11. Minimax ( Generate Tree )

12. Minimax ( Decide Whose Turn ) MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

13. Minimax ( Evaluate Funcions ) 12 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

14. Minimax ( Evaluate Funcions ) 12 7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

15. Minimax ( Evaluate Funcions ) 12 12 7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

16. Minimax ( Evaluate Funcions ) 12 4 12 7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

17. Minimax ( Evaluate Funcions ) 4 12 4 12 7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

18. Minimax ( Evaluate Funcions ) 4 3 12 7 6 3 4 18 6 15 7 24 15 12 5 18 6 7 11 7 24 1 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

19. Minimax ( Evaluate Funcions ) 7 4 3 12 7 6 3 4 18 6 15 7 24 15 12 5 18 6 7 11 7 24 1 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN

20. Minimax ( Evaluate Funcions ) 4 3 12 6 3 4 18 6 15 24 15 12 5 18 6 11 7 24 1 MAX ( Artificial Intelligence ) MIN ( Player ) MAX MIN 7 7 7 7

21. α-β Pruning Extension of Minimax Algorithm. With the help of α-β Pruning we can reduce the size of game tree so we can get quicker response .

22. α-β Pruning If a move is determined worse than another move already examined, then there is no need for further examination of the node.

23. α-β Pruning 11 7 5 1 8 10 16 14 2 MAX ( Artificial Intelligence ) MIN ( Player ) MAX

24. α-β Pruning 7 11 7 5 1 8 10 16 14 2 <7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX

25. α-β Pruning 7 11 7 5 1 8 10 16 14 2 <7 >7 MAX ( Artificial Intelligence ) MIN ( Player ) MAX

26. α-β Pruning 7 11 7 5 1 8 10 16 14 2 <7 >7 <5 MAX ( Artificial Intelligence ) MIN ( Player ) MAX

27. α-β Pruning 7 11 5 7 5 8 10 16 2 <7 >7 <5 In 7<x and 5>x interval there can be no x , so we don’t Need to traverse in nodes 14 and 1 1 14 MAX ( Artificial Intelligence ) MIN ( Player ) MAX

28. α-β Pruning 7 11 7 5 8 MAX ( Artificial Intelligence ) MIN ( Player ) MAX 10 16 2 <7 >7 <5 1 14 <10 In 7<x and 10>x interval there can be x then continue in nodes 2 and 8

29. α-β Pruning 7 11 7 5 8 MAX ( Artificial Intelligence ) MIN ( Player ) MAX 10 16 2 <7 >7 <5 1 14 <2 In 7<x and 2>x interval there can be no x , so we don’t Need to traverse in node 8.

30. α-β Pruning 7 7 11 7 5 8 MAX ( Artificial Intelligence ) MIN ( Player ) MAX 10 16 2 <7 >7 <5 1 14 <2

31. Tic Tac Toe

32. Tic Tac Toe Game Search

33. Applying Minimax & α-β Pruning Evaluation function of Tic Tac Toe game is just win , lose and draw. Computer traverse all nodes until leaf then give every leaf evaluation value. By using minimax method computer select best move. Win by Computer : 1 Win by Opponent : -1 Draw : 0

34. Applying Minimax & α-β Pruning I assume the game state is like above form. Next move will be X and that will be determined by computer using Minimax Method with α-β Pruning step by step.

35. -1 0 0 -1 +1 +1 0 0 MAX ( AI ) MAX ( AI ) MIN ( Opponent ) +1 +1 MIN ( Opponent ) -1 -1 0 0 α-β Pruning Computer Choses That Move

36. ¿ Questions ?

37. Alp Çoker www.alpcoker.com [email_address] Thanks...