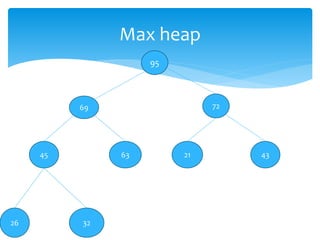
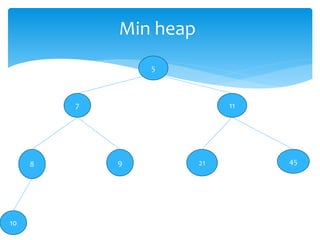
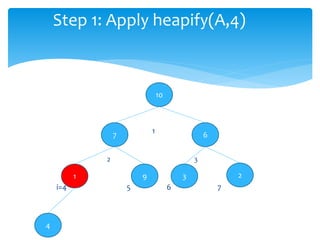
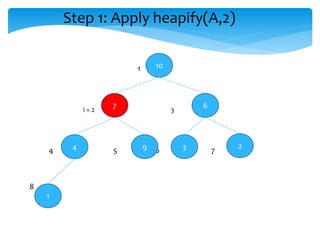
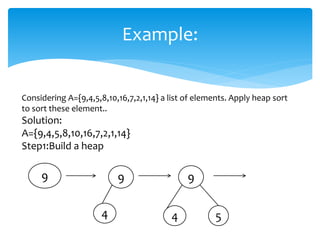
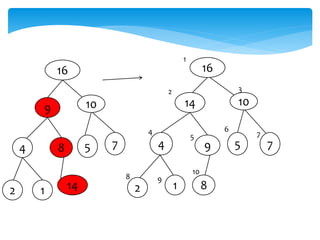
This document describes heap data structures and algorithms like heap sort. It defines a max heap and min heap. It explains the build heap, heapify, insertion and deletion algorithms. Build heap transforms an array into a max heap by applying heapify to each node from bottom to top. Heapify maintains the heap property when a node is added or removed. Heap sort works by building a max heap from the input array and then extracting elements from the root to sort the array in descending order.

1. Heap
Mamotlatsi cloudia Seotsa 37
Saddam Hussain 29
Jyotishna Bora 12

2. contents
1. Binary heap description
2. Applications of heaps
3. Build heap algorithm
4. Heapify alorithm
4.1 Insertion
4.2 Deletion
5. Heap Sort algorithm

3. Binary heap
 A Binary heap is a complete binary tree in which every
node satisfies the heap property which states that :
i. If B is a child of A, then key(A)≥ key (B)
This implies that elements at every node will be greater
than or equal to the element at its left or right child. As
such, the root node has the highest value in the heap.
Such a heap is called a Max-heap

4. ii.
Alternatively, elements at every node will either be less than or
equal to the element at its left and its right child. Thus the root
has the lowest key value. Such a heap is called a Min heap

5. Max heap
95
69 72
45 63 21 43
26 32

6. Min heap
5
7 11
8 9 21 45
10

7.  priority queues
 Graph algorithms like Dijkstra’s algorithm
 Order statistics
applications

8. How to Build a heap
Algorithm
Build_Max_Heap (A)
1. A.Heap_size = A.length
2. For i = A.length/2 down to 1
3. Max_heapify(A,i)
A- an Unsorted Array
i- Array index

9. Example
Consider values: 10, 7, 6, 1, 9, 3, 2 , 4

10. Complete binary tree Representation
.
10
67
4
9 31 2

11. Step 1: Apply heapify(A,4)
1
2 3
i=4 5 6 7
8
10
67
4
9 31 2

12. Step 1: Apply heapify(A,3)
1
2 i= 3
4 5 6 7
8
10
67
1
9 34 2

13. Step 1: Apply heapify(A,2)
1
i = 2 3
4 5 6 7
8
10
67
1
9 34 2

14. Step 1: Apply heapify(A,1)
i=1
2 3
4 5 6 7
8
10
69
1
7 34 2

15.  Heapify is nothing but the procedures of heap.
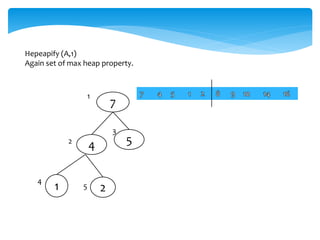
 Heapify is a procedure for manipulating heap data
structures.
 It is given an array A and index i into the array. The sub tree
rooted at the children of A[i] are heap but node A[i] itself
may possibly violate the heap property i.e., A[i] < A[2i] or
A[i] < A[2i +1]. The procedure 'Heapify' manipulates the
tree rooted at A[i] so it becomes a heap. In other words,
'Heapify' is let the value at A[i] "float down" in a heap so
that sub tree rooted at index i becomes a heap.
What is heapify ?

16.  Convert an unordered integer array into a heap array.
 Rearrange a heap to maintain heap property that is
the key of the root node is more extreme (greater or
less) than or equal to the keys of its children.
What does Heapify?

17.  Heapify picks the largest child key and compare it to
the parent key. If parent key is larger than heapify
quits, otherwise it swaps the parent key with the
largest child key. So that the parent is now becomes
larger than its children.
Procedure outline of heapify

18. Understanding the heapify algorithm
with an example

19.  If we put a value at root that is less than every value in the
left and right subtree, then 'Heapify' will be called
recursively until leaf is reached. To make recursive calls
traverse the longest path to a leaf, choose value that make
'Heapify' always recurse on the left child. It follows the left
branch when left child is greater than or equal to the right
child, so putting 0 at the root and 1 at all other nodes, for
example, will accomplished this task. With such values
'Heapify' will called h times, where h is the heap height so
its running time will be θ(h) (since each call does (1) work),
which is (lgn). Since we have a case in which Heapify's
running time (lg n), its worst-case running time is Ω(lgn).
Analysis of heapify

20.  For an array implementation heapify takes O(log n)
time under the comparison model, where n is the
number of nodes & h is the height.
Time and space complexity of
heapify

21. Insertion
Example, Build a max heap H from the given set of
numbers: 56, 23, 28, 56, 72, 64
(step 1) (step 2) (step 3)
56 56
23
56
23 28

22. 56, 23, 28, 51, 72, 64
(step 4) (Step 5)
56
23 28
51
51

23. 56, 23, 28, 51, 72, 64
(step 6) (step 7)
56
51 28
23 72
56
2872
23 51

24. 56, 23, 28, 51, 72, 64
(step 8) (step 9)
72
56
28
21 51 64
72
56 64
21 51
28

25. Array representation
72 56 64 21 51 28

26. Deletion example
Consider a Max heap H shown below and delete the root node
(step 1)
54
45 36
27 29 18 21
11
11
45 36
27 1829 21

27. (Step 3) (Step 4)
45
11 36
27 29 18 21
45
29
11
36
1827 21

28. HEAP SORT
HEAP SORT is a comparison-based sorting algorithm . Heap sort can be
thought of an improved Selection sort , it divides its input into a sorted and an
unsorted region , and it iteratively shrinks the unsorted region by extracting
the largest element and moving that to the sorted region.
HEAPSORT is an in-place algorithm , but it is not a stable sort.

29. HEAPSORT ALGORITHM
HEAPSORT(A)
1. BUILD‐MAX‐HEAP(A)
2. for i ← length[A] downto 2
3. do exchange A[1] A[i]
4. heap‐size[A] ← heap‐size[A] −1
5. MAX‐HEAPIFY(A, 1)

30. Example:
Considering A={9,4,5,8,10,16,7,2,1,14} a list of elements. Apply heap sort
to sort these element..
Solution:
A={9,4,5,8,10,16,7,2,1,14}
Step1:Build a heap
9 9
4
9
4 5

31. 9
4 5
8
9
8 5
4 10
10
9 5
4 8
10
9 5
4 8 16

32. 16
109
4 8 5 7
2 1 14
16
14 10
4 9
2 1 8
5 7
1
2 3
4
5
6
7
8 9
10

33. Array representration
16 14 10 4 9 5 7 2 1 8
1 2 3 4 5 6 7 8 9 10
A

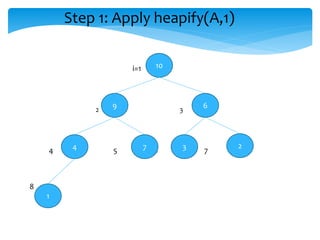
34. Step 2: for i = n to 1 do
Swap( A[1],A[i])
8
14 10
4 9 5 7
2 1 16
Swap(A[1],A[10])
Swap(16,8)

35. Step 3: Set n n-1
Here n=10
n=10-1=9
8
14 10
4 9 5 7
2 1
1
2
3
4
5 6
7
8 9

36. Step 4 : Heapify(A ,1)
i.e. Again set the heap property
14
9 10
4 8 5 7
2 1

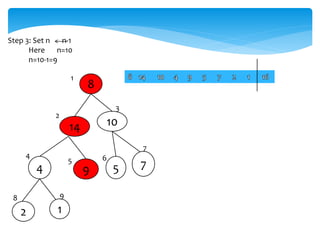
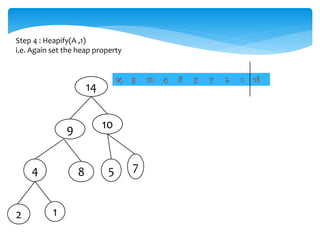
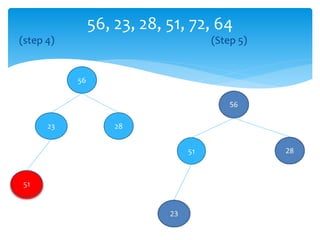
37. Swap(A[1],A[i])
Swap(A[1],A[9])
1
9 10
4 8 5 7
2 14
1
2
3
4
5
6 7
8
9

38. Hepeapify (A,1)
Again set of max heap property.
10
9 7
4 8 5 1
2
1
2
3
4
5
6 7
8

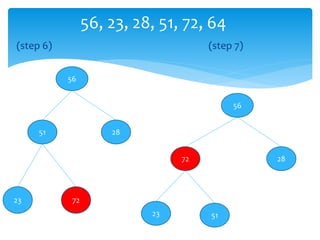
39. Swap(A[1],A[i])
Swap(A[1],A[8])
2
9 7
4 8 5 1
10
1
2
3
4
5
6 7
8

40. n=n-1
8-1=7
2
9 7
4 8 5 1
1
2
3
4
5
6
7

41. Hepeapify (A,1)
Again set of max heap property.
8 7
4 2 5
1
2
3
4
5
6
7
1
9

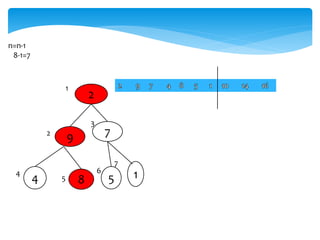
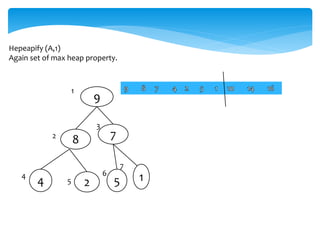
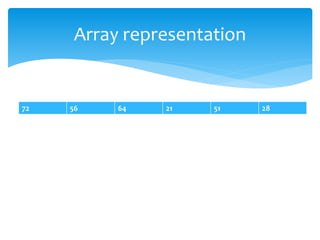
42. Swap(A[1],A[i])
Swap(A[1],A[7])
8 7
4 2 5
1
2
3
5
6
7
9
1
4

43. n=n-1
7-1=6
8 7
4 2
1
2
3
5
6
1
4
5

44. Hepeapify (A,1)
Again set of max heap property.
4 7
1 2 5
1
2
3
6
8
4
5

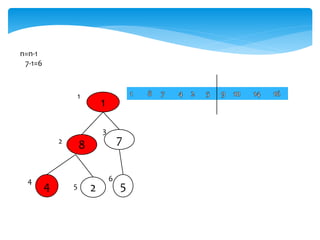
45. Swap(A[1],A[i])
Swap(A[1],A[6])
4 7
1 2 8
1
2
3
6
5
4
5

46. n=n-1
6-1=5
4 7
1 2
1
2
3
5
4
5

47. Hepeapify (A,1)
Again set of max heap property.
4 5
1 2
1
2
3
7
4
5

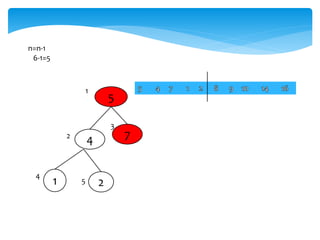
48. Swap(A[1],A[i])
Swap(A[1],A[5])
4 5
1
7
2
3
4
1
2

49. n=n-1
5-1=4
4 5
1
2
3
4
2
1

50. Hepeapify (A,1)
Again set of max heap property.
4 2
1
2
3
4
5
1

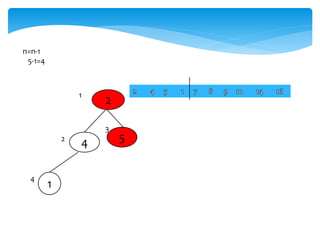
51. Swap(A[1],A[i])
Swap(A[1],[4])
4 22
3
4
1
1
5

52. n=n-1
4-1=3
4 2
2 3
1
1
Hepeapify (A,1)
Again set of max heap property.
1 2
2 3
4
1

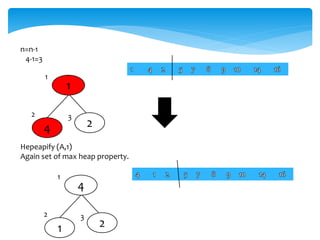
53. Swap(A[1],A[i])
Swap(A[1],[3])
1 4
2 3
2
1
n=n-1
3-1=2
1
2
2
1

54. Swap(A[1],A[i])
Swap(A[1],[2])
2
2
1
1
n=n-1
2-1=1
1
1
SORTED LIST.

55. conclusion
The primary advantage of the heap sort is its efficiency. The
execution time efficiency of the heap sort is O(n log n). The
memory efficiency of the heap sort, unlike the other n log n
sorts, is constant, O(1), because the heap sort algorithm is not
recursive.
The heap sort algorithm has two major steps. The first major
step involves transforming the complete tree into a heap. The
second major step is to perform the actual sort by extracting
the largest element from the root and transforming the
remaining tree into a heap

56.  http://www.wikipedia.org/heap_sort
 Thomas H. C,Charles E. L. (2009)Introduction to
algorithms. Third Edition, ISBN 0-07-013151-1 (McGraw-
Hill)
 http://www.cs.rit.edu/heap_sort
Reference