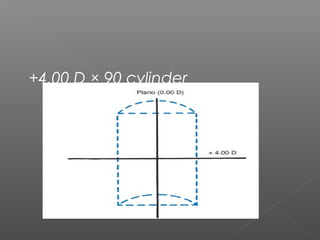
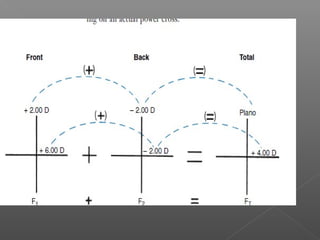
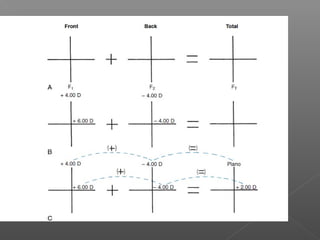
The document discusses different types of lenses based on their curvature and shape. There are two main types: flat lenses, which have one flat surface, and curved lenses, which have curves on both surfaces. Curved lenses include meniscus lenses, which are convex on the front and concave on the back, and toric lenses, where one surface is spherical and the other toroidal. The total power of a lens is calculated by adding the powers of the front and back surfaces. Lens shape refers to the outline and can include round, oval, pantascopic round oval, and upswept shapes.

1.  OPTOM FASLU MUHAMMED

2.  The total power of a lens can be
achieved by combining different types
of curved surfaces (concave or
convex) and this is called the form of
lenses.
 Depending up on the from lenses
could be of two types:
Flat Lenses
Curved Lenses

3.  1. Both its surfaces have got same
type of curvature,e.g. biconcave or
biconvex
 2.One surface is flat and the power is
grounded on the other surface, e.g.
Plano-concave and Plano-convex.

4.  If both surfaces are convex or both
concave, the lens is biconvex or
biconcave.

6.  If one surface is Plano and the other an
outward curved plus surface (i.e., a convex
surface), the lens is referred to as Plano
convex.
 If one surface is Plano and the other
curved inward for minus power (i.e., a
concave surface), the lens is Planoconcave.

8.  A lens is said to be curved when there
is a convex curve on one surface and
a concave curve on the other surface.
 Curved Lenses are of two types:
Meniscus
Toric

9.  These are curved lenses where both
the surfaces are spherical – anterior
surface is convex and posterior
surface is concave.
 Introduction of these lenses has made
mass production of lenses easier.

11.  These are curved lenses where one
surface is spherical and the other
surface is toroidal in shape.
 Toric lenses are used where a
cylinder is also present in the
prescription..

12.  Lenses can be made in a variety of
forms, with many forms possible
for a lens of the same power.

13.  The nominal power of a lens is the sum
of its front and back surface powers.
 When expressed as an equation, this
is
F1 + F2 = F TOTAL

14.  For example, a biconvex lens of +4.00 D
of power could have surface powers,
such as the following:
F1 + F2=F T
(+2.00 D) + (+2.00 D) = +4.00 D
(+3.00 D) + (+1.00 D) = +4.00 D
(+0.50 D) + (+3.50 D) = +4.00 D

15.  The same +4.00 D lens power might then
have any one of the following forms,
which represent only a fraction of the
possibilities.
F1 + F2=F T
(+7.00 D) + (-3.00 D) = +4.00 D
(+8.00 D) + (-4.00 D) = +4.00 D
(+10.00 D) + (-6.00 D) = +4.00 D

16.  These forms are limited only in that
one meridian must have a net power
of zero and the other a net power
equal to the cylinder value.

17. +4.00 D × 90 cylinder

19. Q: Suppose a lens has a toric front
surface. F1 at 90 is +4.00 D , F1 at 180
is +6.00 D .Back surface has a surface
power of−4.00D .What is the total power
of the lens?

21. Q: Suppose a lens has a toric front surface.
F1 at 90 is +4.00 D, and F1 at 180 is +6.00
D. If the back surface has a surface
power of −4.00 D, what is the total power
of the lens?

22.  When the lens obtains its cylinder power
from a difference in power between two
front surface meridians (i.e a toric front
surface lens), the lens is said to be ground
in plus cylinder form.

23.  A lens has a cylinder component, but the
cylinder power is a result of a difference
in power between two back surface
meridians, the lens is said to be ground in
minus cylinder form.

24. Q: If a lens has dimensions of F1 = +6.00 D,
F2 at 90 = −8.00 D, and F2 at 180 = −6.00
D, what form does the lens have and what
is its total power?

27.  Lens shape refers to outline of the lens
periphery with the nasal side and the
horizontal indicated.

28.  Round Lens
- Ancient lens shapes.
-Not much popular
- Still used for some industrial
goggles and other forms of spectacle
in which the fashion element does not
predominate, because it simplifies
glazing.

29.  2.OVAL LENS
- Ancient lens shapes
-Elliptical in shape and not much in
use.

30.  3.Pantoscopic Round Oval (PRO)
 Lower half of a circle and upper half of
an ellipse with the same horizontal
diameter.

31.  It refer to the lens shape which resembles
the monocular field of vision.
 Round contour and the squarer contour

32.  3.Upswept shapes
 4.Rimless or angular shapes
 5. Half -eye shapes.

33. Thank u…..