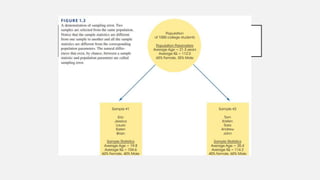
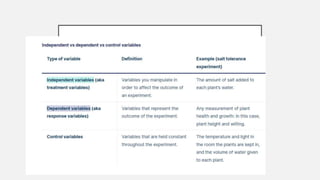
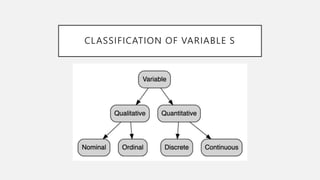
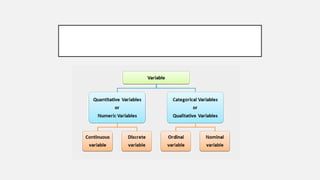
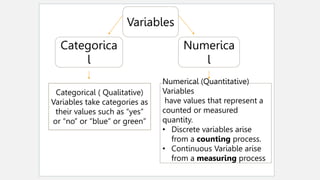
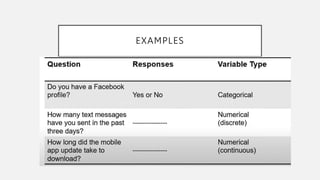
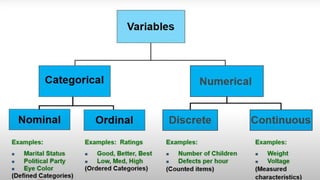
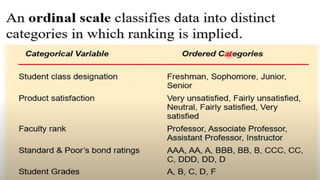
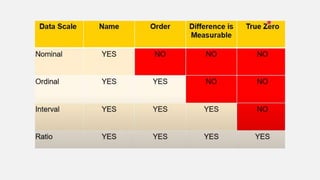
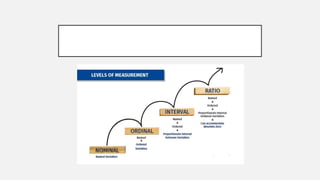
This document provides an overview of topics to be covered in Week 2, including sampling error, types of statistics, types of variables, and a class practice activity. It discusses how sampling error is the naturally occurring discrepancy between a sample statistic and the corresponding population parameter. It also describes descriptive statistics as techniques used to summarize and organize raw data, often through tables and graphs, while inferential statistics allow making generalizations about populations from sample data. Examples are provided of independent and dependent variables that could be measured in a plant study. Finally, different types of variable scales are defined.

1. WEEK 2

2. WE WILL LEARN
• Sampling Error
• Types of Statistics
• Types of Variables
• Class Practice

3. SAMPLING ERROR
• Because populations are typically very large, it usually is not possible to
measure everyone in the population. Therefore, a sample is selected to
represent the population. By analyzing the results from the sample, we
hope to make general statements about the population. Typically,
researchers use sample statistics as the basis for drawing conclusions
about population parameters. One problem with using samples,
however, is that a sample provides only limited information about the
population. Although samples are generally representative of their
populations, a sample is not expected to give a perfectly accurate
picture of the whole population. There usually is some discrepancy
between a sample statistic and the corresponding population parameter.
This discrepancy is called sampling error, and it creates the fundamental
problem inferential statistics must always address.

4. SAMPLING ERROR
• Sampling error is the naturally occurring discrepancy, or error, that
exists between a sample statistic and the corresponding population
parameter.

5. EXAMPLE

6. DESCRIPTIVE AND INFERENTIAL
STATISTICAL METHODS
• Although researchers have developed a variety of different statistical
procedures to organize and interpret data, these different procedures
can be classified into two general categories. The first category,
descriptive statistics, consists of statistical procedures that are used to
simplify and summarize data.
• Descriptive statistics are statistical procedures used to summarize,
organize, and simplify data.

7. • Descriptive statistics are techniques that take raw scores and organize or
summarize them in a form that is more manageable. Often the scores
are organized in a table or a graph so that it is possible to see the entire
set of scores.
• The second general category of statistical techniques is called inferential
statistics. Inferential statistics are methods that use sample data to make
general statements about a population.
• Inferential statistics consist of techniques that allow us to study
and then make generalizations about the populations from which
were selected.

8. EXAMPLE

9. EXAMPLE
• If you want to test whether some plant species are more salt-tolerant
than others, some key variables you might measure include the amount
of salt you add to the water, the species of plants being studied, and
variables related to plant health like growth and wilting.

10. TYPES OF VARIABLES

12. CLASS PRACTICE
• You all are requested to do some thinking and come up with 5 examples
indicating IV, and DV.

13. CLASSIFICATION OF VARIABLE S

15. Variables
Categorica
l
Numerica
l
Categorical ( Qualitative)
Variables take categories as
their values such as “yes”
or “no” or “blue” or green”
Numerical (Quantitative)
Variables
have values that represent a
counted or measured
quantity.
• Discrete variables arise
from a counting process.
• Continuous Variable arise
from a measuring process

16. EXAMPLES

19. NOMINAL SCALE
• Assigning numbers to objects where different numbers
indicate different objects.
• The numbers have no real meaning other than
differentiating between objects.
• Example: Gender, Male=1, Female=2
Baseball uniform number

21. ORDINAL SCALE
• Assign numbers to objects, but these numbers have
meaningful order.
• Example; Athletes, Race finishing order1st 2nd 3rd ( the
number indicates their performance)

22. INTERVAL SCALE

23. INTERVAL SCALE
• Numbers have orders ( like ordinal), there are also equal intervals
between adjacent categories.
• Example; temperature in degrees Fahrenheit; the difference between 78
degree and 79 degree ( 1 degree) is the as 45 and 46 degree.

24. RATIO SCALE

25. RATIO SCALE
• Differences are meaningful ( like interval), plus ratios are meaningful but
there is a true zero point.
• Example 0 inches means no height ( or absence of height)

28. • THANK YOU!