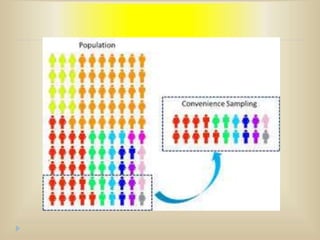
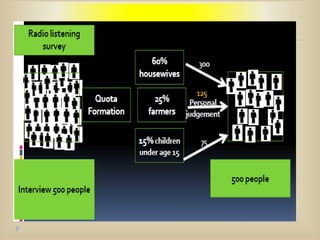
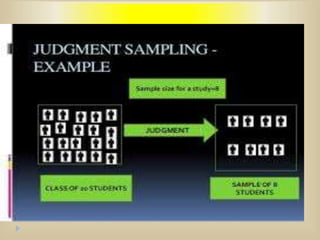
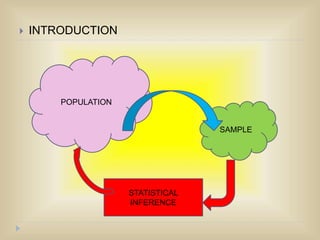
The document outlines various sampling techniques and their significance in research, distinguishing between probability and non-probability sampling methods. It details the merits and demerits of different sampling designs such as simple random sampling, stratified sampling, cluster sampling, and more, alongside statistical concepts such as parameters and sampling errors. The text emphasizes the importance of proper sampling methods for accurate statistical inference and the challenges of obtaining representative samples.

1. DR ANKITA CHATURVEDI

2. SAMPLING TECHNIQUES
CONTENTS :
 Introduction
 Parameter and statistics
 Sampling Errors
 Sampling Process
 Methods of Sampling
>>Probability Sampling
>>Non Probability Sampling

3.  INTRODUCTION
POPULATION
SAMPLE
STATISTICAL
INFERENCE

4. POPULATION
 The entire aggregation of items from which samples
can be drawn is known as a population.
 In sampling, the population may refer to the units,
from which the sample is drawn.
 Thus, population could consists of all the persons in
the country, or those in a particular geographical
location or a special economic group, depending on
the purpose and coverage of the study.
 This is one of the first things the analyst needs to
define properly while conducting a business
research.
 “N” represents the size of the population.

5. SAMPLING
 In simple words, sampling consists of obtaining
information from a portion of a larger group or an
universe. Elements are selected in a manner that they yield
almost all information about the whole universe, if and
when selected according to some scientific principles and
procedures.

6. CENSUS
A complete study of all the elements present in the
population is known as a census. The national population
census is an example of census survey
Merits
1. Data obtained from each and every unit of population.
2. Results: more representative, accurate, reliable.
3. Basis of various surveys.
Demerits
1. More effort ,money , time.
2. Big problem in underdeveloped countries.

7. SAMPLE
A Sample is a selection of units from the entire group called
the population or universe of interest. It is Subset of a
larger population
Merits
1. Less resources (time, money)
2. Less workload.
3. Gives results with known accuracy that can be
calculated mathematically.
Demerits
1. Difficulties of a representative sample
2. Need for specialized knowledge
3. Chances of bias

10.  The population criteria establish the target population;
that is, the entire set of cases about which the researcher
would like to make generalizations.
Statistical Inference
 Statistical inference is the process of drawing
conclusions about the entire population based on
information in a sample.

11. (Population) Parameters
 A parameter is a value used to describe a certain
characteristic of a population. It is usually unknown and
therefore has to be estimated.
 For example, the population mean is a parameter that is
often used to indicate the average/typical value of a
variable in the population.

12. (Sample) statistics
 A statistic is an estimate, based on a sample of observed
data, of a population parameter.
 The statistic is drawn from the measurement of the
elements of the sample.
 A statistic is used to estimate a parameter. The more
samples you have, the better your estimation.

14. Sampling Error
 Since a sample does not include all members of the
population, parameter estimates generally differ from
parameters on the entire population (e.g., use mean height
of a sample of 1000 people to estimate mean height of
Indian population).
 The difference between the (sample) statistics estimate
and the (population) parameter is sampling error.

15. SAMPLING DESIGN PROCESS

16. PROBABILITY
SAMPLING

17. PROBABILITY SAMPLING
 A probability sampling scheme is one in which every
unit in the population has a chance (greater than zero) of
being selected in the sample, and this probability can be
accurately determined.
 Universe is identified.
 . When every element in the population does have the
same probability of selection, this is known as an 'equal
probability of selection' (EPS) design. Such designs are
also referred to as 'self-weighting' because all sampled
units are given the same weight.
 Only Parametric Tests can be applied
 Results may be generalized

18. PROBABILITY SAMPLING
Probability sampling includes:
 Simple Random Sampling,
 Stratified Random Sampling,
 Cluster Sampling
 Systematic Sampling,
 Multistage Sampling.

19. SIMPLE RANDOM SAMPLING
• Applicable when population is small, homogeneous &
readily available
• All subsets of the frame are given an equal probability.
Each element of the frame thus has an equal probability of
selection.
• It provides for greatest number of possible samples. This
is done by assigning a number to each unit in the sampling
frame.
• A table of random number or lottery system is used to
determine which units are to be selected.

20. SIMPLE RANDOM SAMPLING
LOTTERY METHOD RANDOM NUMBER TABLE

21. SIMPLE RANDOM SAMPLING
Merits
 No personal bias.
 Sample more representative of population.
 Accuracy can be assessed as sampling errors follow
principals of chance.
Demerits
 If sampling frame large, this method impracticable
 Requires completely catalogued universe.
 Cases too widely dispersed - more time and cost.

22. STRATIFIED RANDOM SAMPLING
 Stratified random sampling is a method of probability
sampling in which the population is divided into different
subgroups and samples are selected from each of them.
 Applicable when population is large and heterogeneous
 Where population embraces a number of distinct
categories, the frame can be organized into separate
"strata." Each stratum is then sampled as an independent
sub-population, out of which individual elements can be
randomly selected.
 Every unit in a stratum has same chance of being selected.

23. STRATIFIED RANDOM SAMPLING
 Using same sampling fraction for all strata ensures
proportionate representation in the sample.
 Adequate representation of minority subgroups of interest
can be ensured by stratification & varying sampling
fraction between strata as required.

26. STRATIFIED RANDOM SAMPLING
Merits:
 It provides better coverage of the population since
the researchers have control over the subgroups to
ensure all of them are represented in the sampling.
 A stratified sample can provide greater precision than
a simple random sample of the same size.
 Because it provides greater precision, a stratified
sample often requires a smaller sample, which saves
money.
 A stratified sample can guard against an
"unrepresentative" sample (e.g., an all-male sample
from a mixed-gender population).
 We can ensure that we obtain sufficient sample points
to support a separate analysis of any subgroup.

27. STRATIFIED RANDOM SAMPLING
Demerits
 sampling frame of entire population has to be prepared
separately for each stratum
 when examining multiple criteria, stratifying variables
may be related to some, but not to others, further
complicating the design, and potentially reducing the
utility of the strata.
 in some cases (such as designs with a large number of
strata, or those with a specified minimum sample size per
group), stratified sampling can potentially require a larger
sample than would other methods

28. CLUSTER SAMPLING
 Cluster sampling is an example of 'two-stage
sampling' .
 First stage a sample of areas is chosen;
 Second stage a sample of respondents within those
areas is selected.
 Population divided into clusters of homogeneous units,
usually based on geographical contiguity.
 Sampling units are groups rather than individuals.
 A sample of such clusters is then selected.
 All units from the selected clusters are studied.

30. CLUSTER SAMPLING
Merits
 Cuts down on the cost of preparing a sampling frame.
 This can reduce travel and other administrative costs.
Demerit
 sampling error is higher for a simple random sample of
same size.

31. STRATIFIED CLUSTER SAMPLING
 Combines elements of stratification and clustering
 First we define the clusters
 Then we group the clusters into strata of clusters, putting
similar clusters together in a stratum
 Then we randomly pick one (or more) cluster from each of
the strata of clusters
 Then we sample the subjects within the sampled clusters
(either all the subjects, or a simple random sample of
them)
 Advantage: Reduce the error in cluster sampling by
creating strata of clusters

32. STRATIFICATION v/s CLUSTER
Stratification
 Divide population into
groups different from
each other: sexes,
races, ages
 Sample randomly from
each group
 Less error compared to
simple random
 More expensive to
obtain stratification
information before
sampling
Clustering
 Divide population into
comparable groups:
schools, cities
 Randomly sample
some of the groups
 More error compared to
simple random
 Reduces costs to
sample only some areas
or organizations

33. With stratified sampling, the best survey results
occur when elements within strata are internally
homogeneous. However, with cluster sampling,
the best results occur when elements within
clusters are internally heterogeneous

34. SYSTEMATIC SAMPLING
 Systematic sampling relies on arranging the target
population according to some ordering scheme and
then selecting elements at regular intervals through
that ordered list.
 Systematic sampling involves a random start and then
proceeds with the selection of every kth element from
then onwards. In this case, k=(population size/sample
size).
 It is important that the starting point is not
automatically the first in the list, but is instead
randomly chosen from within the first to the kth
element in the list.
 A simple example would be to select every 10th name
from the telephone directory (an 'every 10th' sample,
also referred to as 'sampling with a skip of 10').

35. SYSTEMATIC SAMPLING
As described above, systematic sampling is an EPS method,
because all elements have the same probability of selection (in
the example given, one in ten). It is not 'simple random
sampling' because different subsets of the same size have
different selection probabilities - e.g. the set {4,14,24,...,994}
has a one-in-ten probability of selection, but the set
{4,13,24,34,...} has zero probability of selection.

36. SYSTEMATIC SAMPLING
Merits:
 Sample easy to select
 Suitable sampling frame can be identified easily
 Sample evenly spread over entire reference population
Demerits:
 Sample may be biased if hidden periodicity in
population coincides with that of selection.
 Difficult to assess precision of estimate from one
survey.

37. MULTISTAGE SAMPLING
 Complex form of cluster sampling in which two or
more levels of units are embedded one in the other.
 First stage, random number of districts chosen in all
states.
 Followed by random number of talukas, villages.
 Then third stage units will be houses.
 All ultimate units (houses, for instance) selected at
last step are surveyed.

39. MULTISTAGE SAMPLING
 This technique, is essentially the process of taking random
samples of preceding random samples.
 Not as effective as true random sampling, but probably
solves more of the problems inherent to random sampling.
 An effective strategy because it banks on multiple
randomizations. As such, extremely useful.
 Multistage sampling used frequently when a complete list
of all members of the population not exists and is
inappropriate.
 Moreover, by avoiding the use of all sample units in all
selected clusters, multistage sampling avoids the large,
and perhaps unnecessary, costs associated with traditional
cluster sampling.

40. IDENTIFY WHAT TYPE OF SAMPLING IS
THIS…
1. A student council surveys 100 students by getting
random samples of 25 I year, 25 II year, 25 III year,
and 25 PG
2. An airline company wants to survey its customers
one day, so they randomly select 5 flights that day
and survey every passenger on those flights
3. A teachers puts students' names in a hat and
chooses without looking to get a sample of
students.
4. A principal takes an alphabetized list of student
names and picks a random starting point. Every
20th student is selected to take a survey

41. 5. Each student at a school has a student identification
number. Counselors have a computer generate 50
random identification numbers and those students
are asked to take a survey
6. A principal orders t-shirts and wants to check some
of them to make sure they were printed properly. She
randomly selects 2 of the 10 boxes of shirts and
checks every shirt in those 2 boxes.
7. A school chooses 3 randomly selected athletes from
each of its sports teams to participate in a survey
about athletics at the school.

42. Answers
1. Stratified Random Sampling
2. Cluster Sampling
3. Simple Random Sampling
4. Systematic Sampling
5. Simple Random Sampling
6. Cluster Sampling
7. Stratified Random Sampling

43. Non-PROBABILITY
SAMPLING

44. NON PROBABILITY SAMPLING
 Every element in the universe [sampling frame] does not
have equal probability of being chosen in the sample
 Universe is unidentified
 It involves the selection of elements based on assumptions
regarding the population of interest, which forms the
criteria for selection. Hence, because the selection of
elements is nonrandom, nonprobability sampling not
allows the estimation of sampling errors.
 Only Non- Parametric Tests can be applied.
 Results may not be generalized.

45. NON PROBABILITY SAMPLING
Non Probability sampling includes:
 Convenience Sampling
 Quota Sampling
 Judgmental Sampling (Purposive Sampling)
 Snowball sampling

46. CONVENIENCE SAMPLING
 Convenient sample units selected.
 Selected neither by probability nor by judgment.
Merit
 useful in pilot studies.
Demerit
 results usually biased and
 unsatisfactory.

48. QUOTA SAMPLING
 Most commonly used in non probability sampling.
 The population is first segmented into mutually exclusive
sub-groups, just as in stratified sampling.
 Then judgment used to select subjects or units from each
segment based on a specified proportion.

50. QUOTA SAMPLING
Merits
 Used when research budget is limited
 Very extensively used/understood
 No need for list of population elements
Disadvantages
 Variability and bias cannot be measured/controlled
 Time Consuming
 Projecting data beyond sample not justified

51. JUDGMENTAL SAMPLING
 Judgment/Purposive/Deliberate sampling.
 Depends exclusively on the judgment of investigator.
 Sample selected which investigator thinks to be most
typical of the universe.
 This is used primarily when there is a limited number of
people that have expertise in the area being researched

53. JUDGMENTAL SAMPLING
Merits
 Small no. of sampling units
 Study unknown traits/case sampling
 Urgent public policy & business decisions
Demerits
 Personal prejudice & bias
 No objective way of evaluating reliability of results

54. SNOWBALL SAMPLING
 A special non probability method used when the
desired sample characteristic is rare.
 The research starts with a key person and introduce
the next one to become a chain

55. SNOWBALL SAMPLING- STEPS
 Make contact with one or two cases in the population.
 Ask these cases to identify further cases.
 Ask these new cases to identify further new cases.
 Stop when either no new cases are given or the sample is
as large as is manageable

56. Merit
 access to difficult to reach populations (other
methods may not yield any results).
Demerit
 not representative of the population and will result in
a biased sample as it is self-selecting.

57. Types of Sampling Errors
Two types of sampling errors
 Biased Errors- Due to selection of sampling
techniques; size of the sample.
 Unbiased Errors / Random sampling errors-
Differences between the members of the population
included or not included.

58. METHODS OF REDUCING SAMPLING
ERRORS
 Specific problem selection.
 Systematic documentation of related research.
 Effective enumeration.
 Effective pre testing.
 Controlling methodological bias.
 Selection of appropriate sampling techniques