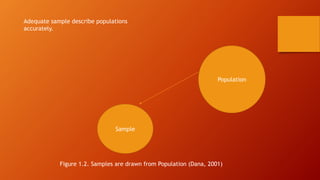
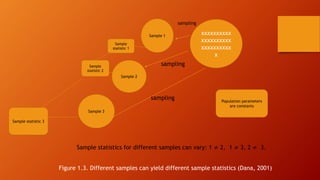
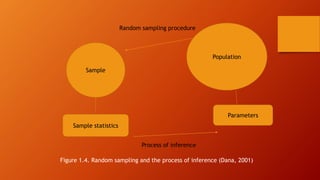
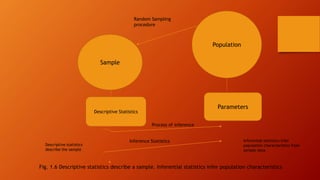
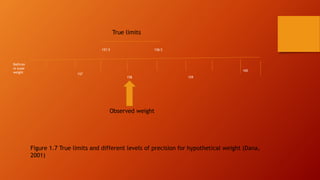
This document discusses statistics and data analysis as tools for researchers. It defines key concepts such as variables, constants, populations, samples, descriptive statistics, and inferential statistics. Descriptive statistics are used to describe samples, while inferential statistics allow generalizing about populations from samples. Random sampling is emphasized as it allows each population member an equal chance of being selected. The scientific method, involving hypotheses testing, is also discussed. Statistics and data analysis provide a systematic way to examine data and gain insights, though they do not prove definitive conclusions.

1. STATISTICS AND DATA ANALYSIS
AS TOOLS FOR RESEARCHERS
INTRODUCTION
By Desmond Ayim-Aboagye, PhD

2. THEORIES OF STATISTICS & ANALYSIS OF DATA
• How to select an appropriate Statistical test
• How to collect the right kinds of information for analysis
• How to perform statistical calculations in a straightforward, step
by step manner.
• How to accurately interpret and present statistical results.
• How to be an intelligent consumer of statistical information.
• How to write up analyses and results in American Psychological
Association (APA) style. (Dana S. Dunn, 2001)

3. A Statistic
• A statistic is some piece of information that is presented in
numerical form. For example, a nation’s 5% unemployment rate is
a statistic, and so is the average number of words per minute read
by a group of second-grades or the reported high temperature on
july day in June.

4. Data Analysis
• Data analysis refers to the systematic examination of a collection
of observations. The examination can answer a question, search
for a pattern, or otherwise make sense out of the observations.

5. Statistic and Data Analysis
• Statistic and data analysis are complementary, but not equivalent
terms.
• Example: Quantitative and Qualitative
• Quantitative relationships are numerical.
• Qualitative relationships are based on descriptions or organizing
themes, not numbers.

6. A Variable
• A variable is any factor that can be measured or have a different
value. Such factors can vary from person to person, place to
place, experimental situation to experimental situation.
• Example:
• a. Hair color can be a variable (blonde, brunette, redhead)
• b. The day of the week
• c. Weight

7. A Constant
• A constant is usually a number whose value does not change.
• Example 𝜋 (pronounce “pie”) which equals 3.1416
• It can also refer to a characteristic pertaining to a person or
environment that does not change.

8. Variables and Constant
• Variables take on different
values
• Constants do not change

9. Statistics and Data Analysis
• Statistics and data analysis highlight possible solutions or answers
to questions, not absolute or definitive conclusions.

10. Statistics and Mathematics
• Statistics is not equal to mathematics (Statistics ≠ Mathematics)
• Statistics is the science of data, not mathematics.
• “The field of statistics is concerned with making sense out of
empirical data , particularly when those data contain some
element of uncertainty so that we do not know the true state of
affairs, how, say a set of variables affect one another” (Dana,
2001)

11. EMPIRICAL
• Empirical refers to anything derived from experiences or
experiment.

12. Statistic, Data Analysis, & Scientific Method
• Researchers in the behavioral sciences use statistics to analyze
data collected within the framework of the scientific method.
• The Scientific method: The scientific method guides research by
identifying a problem, formulating a hypothesis, and collecting
empirical data to test the hypothesis.

13. A Hypothesis
• A hypothesis is a testable question or prediction, one usually
designed to explain some phenomenon.
• Examples:
• A. There is an association between the color of the skin and the
continent where a person comes from.
• B. Individuals who hails from broken homes tend to be criminals.
• C. Children who watch violent films grow up to become aggressive
individuals.

14. A Theory
• A theory is a collection of related facts, often derived from
hypotheses and the scientific method, forming a coherent
explanation for a larger phenomenon.
• Examples:
• A. The Theory of Aggression
• B. The Theory of Cognitive Dissonance (Leon Festinger)
• C. The life Cycle Theory (Erik Eriksson)
• D. Operant Condition (Pavlov)

15. INDUCTIVE AND DEDUCTIVE REASONING
• Inductive: Genralizing from one or more observations in the course
of developing a more general explanation.
• Observations are used to generate theories.
• Induction data lead to theory
• Psychology, economics, education, sociology, and anthropology
often rely on inductive reasoning (Dana, 2001: p.10 f.)

16. Deductive Reasoning/method
• Deductive reasoning is characterized by the use of existing
theories to develop conclusions, called deductions, about how
some unexamined phenomenon is likely to operate.
• Theory is used to search for confirming observations (hypotheses).
• Deduction: Theory leads to data

17. THEORY (Generalizations)
Inductive reasoning
Deductive reasoningxxx Observations
xxxx

18. POPULATIONS AND SAMPLES
SAMPLING PROCEDURES

19. A Population
• A population is a complete set of data possessing some observable
characteristic, or a theoretical set of potential observations.

20. A Sample
• A sample is a smaller unit or subset bearing the same
characteristic or characteristics of the population of interest.

21. Population
Sample
Figure 1.2. Samples are drawn from Population (Dana, 2001)
Adequate sample describe populations
accurately.

22. A Population Parameter
• A population parameter is a value that summarizes some
important, measurable characteristic of a population. Although
population parameters are estimated from statistics, they are
constants.
• Parameters are estimated but they do not change.

23. A Sample Statistic
• A sample statistic is a summary value based upon some measurable
characteristic of a sample.
• The value of sample statistics can vary from sample to sample.
• Statistics are calculated from sample data, and they change from sample
to sample.
• “Although sample statistics are apt to change from sample to sample, a
parameter, such as a population average, will not change.” (Dana, 2001;
p. 14)

24. SAMPLE RANDOM SAMPLING
• Sampling random sampling is a process whereby a subset is drawn
from a population in such a way that each member of the
population has the same opportunity of being selected for
inclusion in the subset as all the others.

25. xxxxxxxxxx
xxxxxxxxxx
xxxxxxxxxx
x
Sample 1
Sample 2
Sample 3
Sample
statistic 1
Sample
statistic 2
Sample statistic 3
Population parameters
are constants
Sample statistics for different samples can vary: 1 ≠ 2, 1 ≠ 3, 2 ≠ 3.
Figure 1.3. Different samples can yield different sample statistics (Dana, 2001)
sampling
sampling
sampling

26. Population
Sample
Sample statistics
Parameters
Process of inference
Random sampling procedure
Figure 1.4. Random sampling and the process of inference (Dana, 2001)

27. Descriptive and Inferential Statistics
Descriptive Statistics

28. Descriptive and Inferential Statistics
• Descriptive statistics are
statistical procedures that
describe, organize, and
summarize the main
characteristics of sample data.
• Descriptive statistics describe
samples
• Inferential statistics permit
generalizations to be made
about populations based on
sample data drawn from them.
• Inferential statistics infer
population characteristics.

29. Population
Sample
Parameters
Descriptive Statistics
Process of inference
Inference Statistics
Random Sampling
procedure
Descriptive statistics
describe the sample
Inferential statistics infer
population characteristics from
sample data
Fig. 1.6 Descriptive statistics describe a sample. Inferential statistics infer population characteristics

30. Discontinuous and Continuous Variables
• A discontinuous variable is countable,
and it has gaps between each number
where no intermediate values can occur
(discrete variables)
• Examples:
• Participants response e.g 1 = yes, 2 = no,
3 = other
• Description, eg 1 = first year, 2 =
sophomore, 3 = junior, 4 = senior, 5 =
other
• A continuous variable can take on any
numerical value on a scale, and there
exists an infinite number of values
between any two numbers on a scale.
• Examples:
• GPA 4.0 = A, 3.67 = B+ etc

31. True limit
• True limits are a range of values within which a true value for
some variable is contained.
• True limits are calculated by taking the value of a continuous
variable and then adding and subtracting one half of the unit of
measurement from it.
• True limits are sometimes called real limits.
• True limit delineate a range of values where a true value of some
variable is presumably located.
• Lower true limit– Upper true limit

32. Figure 1.7 True limits and different levels of precision for hypothetical weight (Dana,
2001)
Bathroo
m scale
weight 157
158 159
160
Observed weight
157.5 158.5
True limits