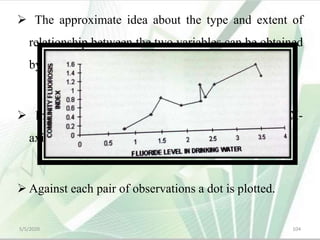
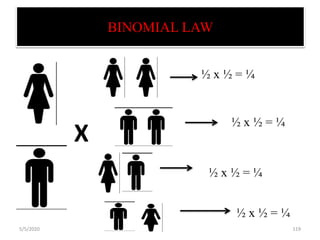
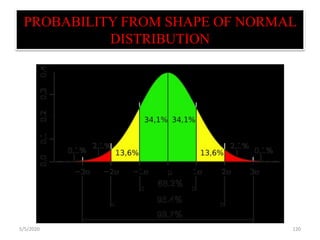
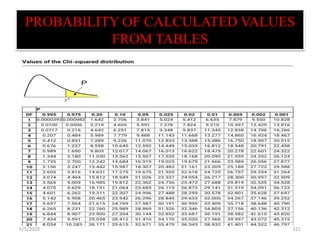
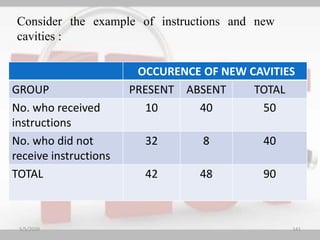
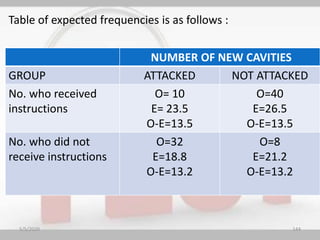
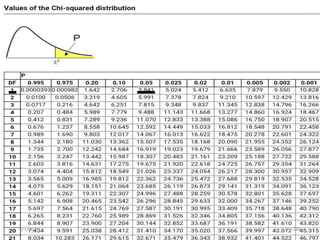
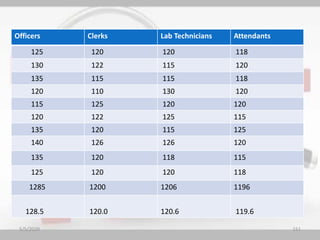
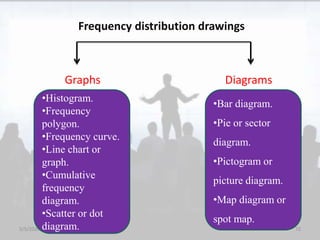
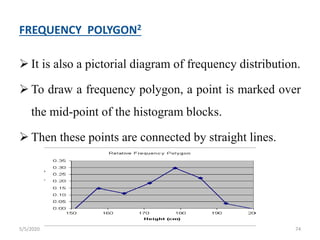
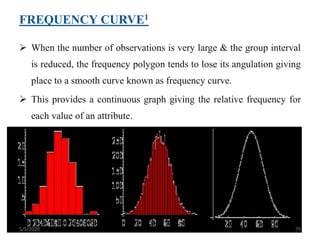
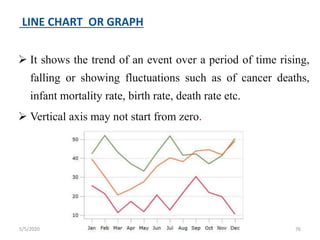
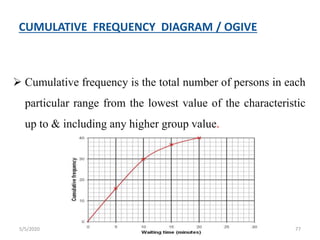
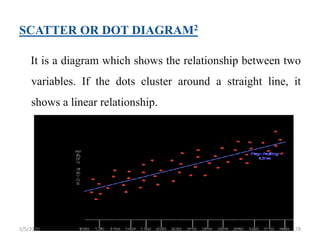
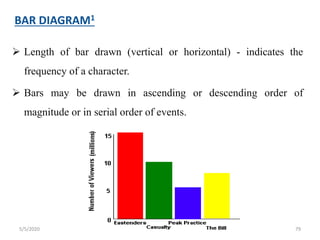
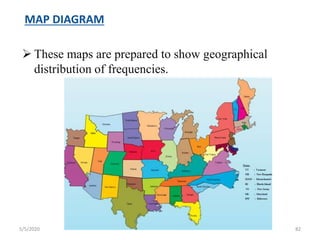
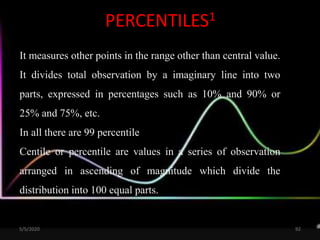
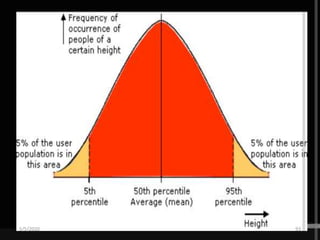
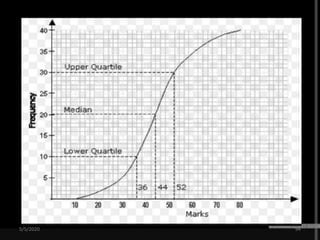
The document discusses the importance and principles of biostatistics in medical science, emphasizing its role in analyzing and interpreting health-related data. It covers various statistical methods such as measures of central tendency, sampling techniques, and data presentation methods useful in epidemiological studies. Furthermore, it highlights the applications of biostatistics in public health, clinical research, and the evaluation of health interventions.


















































































![STANDARD DEVIATION1
It is a improvement over mean deviation as a measure
of dispersion.
It is most frequently used measure of deviation in
statistical analyses.
Denoted by the Greek letter sigma (σ).
Formula:
S.D.= √variance= √Σ(x-x)2/η-1 or
= √[Σx2-(Σx)2/η]/n-1
5/5/2020 99](https://image.slidesharecdn.com/biostatistics-200505055325/85/Biostatistics-99-320.jpg)
![E.g.,
Find SD of ESR, found to be 3, 4, 5, 4, 2, 4, 5 & 3 in 8
normal individuals.
Sum of observations or
ΣX=3+4+5+4+2+4+5+3=30
Sum of squares of observations or
ΣX2=9+16+25+16+4+16+25+9= 120
variance(s2)= [ΣX2-(ΣX)2/n ]/n-1
= [120-(30)2/8]/8-1
= 120-112.5/7=7.5/7
s=7.5/7=√1.07=1.03
5/5/2020 100](https://image.slidesharecdn.com/biostatistics-200505055325/85/Biostatistics-100-320.jpg)