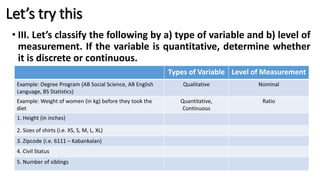
Statistics is the study of collecting, organizing, summarizing, and interpreting data. It involves defining populations and samples, variables and observations, parameters and statistics. There are two main fields - descriptive statistics which summarizes data, and inferential statistics which analyzes samples to generalize to populations. Variables can be qualitative like gender or quantitative like height. Quantitative variables can be discrete like number of siblings or continuous like weight. Measurement scales range from nominal to ratio levels.

1. Basic Concepts in
Statistics
......DownloadsY2Mate.is - Why You Need to Study Statistics-wV0Ks7aS7YI-720p-1647268556411.mp4

2. • Why Study Statistics?
• To evaluate printed numerical facts.
• To interpret the results of sampling or to perform statistical
analysis in your work
• To make inferences about the population using information
collected from the sample
• What Do Statisticians Do?
• Gather data
• Summarize data
• Analyze data
• Draw conclusions and report the results of their analysis

3. Statistics
•A. Definition of Statistics
• Plural sense – set of numerical figures e.g. number of students
enrolled in every program in CPSU, vital statistics in a beauty
contest
• Singular sense – the branch of science that deals with the
collection, presentation, organization, analysis, and
interpretation of data (COPAI)
•B. Key Terms
• Population – (denoted by N) the collection of all elements
under consideration
• Sample – (denoted by n) a subset of the population

4. Statistics
•Example:
• A manufacturer of kerosene heaters wants to determine if
customers are satisfied with the performance of their heaters.
Toward this goal, 5,000 out of 200,000 customers are contacted
and each is asked, "Are you satisfied with the performance of
the kerosene heater you purchased?" Identify the population
and the sample for this situation.
• Population:
• The collection of 200,000 kerosene heater customers.
• Sample:
• The collection of 5,000 kerosene heater customers who
were interviewed.

5. Statistics
•Variable – a characteristic or attribute of the elements in a
collection that can assume different values for the different
elements.
• Example: Age, Weight, Height
•Experimental unit is the individual or object on which a
variable is measured.
• Example:
• Age (in years) of a freshman student
• Weight (in kilograms) of mangoes harvested
• Height (in inches) of a sugarcane plant in 3 months

6. Statistics
•Observation – realized value of a variable
•Data – collection of observations
VARIABLE POSSIBLE OBSERVATION
a. S = sex of a student Male, Female
b. C = course of a student AB Eng, AB Soc Sci, BS Stat
c. L = amount spent on load per month 𝐿 ≥ 0 pesos
d. N =number of enrolled students per
campus
n = 0, 1, 2, 3, …
e. H = height of a volleyball player h > 0 cm

7. Statistics
•Parameter – a summary measure describing specific
characteristic of the population usually denoted by Greek
letters: μ (mu), σ (sigma), ρ (rho), λ (lambda), τ (tau), θ
(theta), α (alpha) and β (beta) e.g. population mean,
population variance
•Statistic – a summary measure describing specific
characteristic of the sample
• e.g. sample mean, sample variance

9. Statistics
•Example: In order to estimate the true proportion of
students at a certain college who smoke cigarettes, the
administration polled a sample of 200 students and
determined that the proportion of students from the
sample who smoke cigarettes is 0.12. Identify the a)
population, b) sample, c) parameter, and d) statistic.
• a) Population: The set of students at a certain college.
• b) Sample: The set of 200 students who were interviewed.
• c) Parameter: The population proportion of students in a certain college
who smoke cigarettes.
• d) Statistic: (0.12) the proportion of students in the sample who smoke
cigarettes.

10. C. Fields of Statistics
•1. Statistical Methods of Applied Statistics - procedures
and techniques used in the collection, presentation,
analysis and interpretation of data.
•2. Statistical Theory of Mathematical Statistics - deals
with the development and exposition of theories that
serve as bases of statistical methods.
• a. Descriptive Statistics – includes all the techniques used in
organizing, summarizing, and presenting the data on hand.
• b. Inferential Statistics – includes all the techniques used in
analyzing the sample data that will lead to generalizations
about a population from which the sample came from

11. C. Fields of Statistics
•Example
Descriptive Inferential
1. A bowler wants to find his bowling
average for the past 12 games.
1. A bowler wants to estimate his chance of
winning a game based on his current season
averages and the averages of his opponent.
2. A housewife wants to determine the
average weekly amount she spent on
groceries in the past three months.
2. A housewife would like to predict based
on last year's grocery bills, the average
weekly amount she will spend for this year.
3. A politician wants to know the exact
number of votes he received in the last
election.
3. A politician would like to estimate, based
on an opinion poll, his chance of winning in
the upcoming election.

12. D. Measurement
•Measurement - the process of determining the value
or label of a variable based on what has been
observed
•Example:
• Age (in years)
• Weight (in kilograms)
• Height (in inches)
• Sex (Male or Female)

13. Types of Variables
•1. Qualitative variable
•A variable that yields categorical response
•Describes the quality or character of something
• Example: Eye color, First Name, Favorite Movie
•2. Quantitative Variable
•A variable that takes on numerical values representing
an amount or quantity
•Describes the amount or number of something
• Example: Weight, Height, Number of cars

14. Types of Variables
•a. Discrete - a variable which can assume finite, or, at
most, countably infinite number of values; usually
measured by counting or enumeration.
•Can assume only certain values, and there are
usually gaps between values.
•Example: Number of students enrolled in GEC 4,
Number of cars parked at the front of Admin building

15. Types of Variables
•b. Continuous - a variable which can assume
infinitely many values corresponding to a line
interval without gaps, interruptions, or jumps.
•Can assume any value within a specified range.
•Measurable (measured using a continuous scale such
as kilos, centimeters, grams)
•Example: Height in inches, Income in pesos, Weight in
kilograms

16. Levels of Measurement
•1. Nominal Level (Classificatory Scale)
•The nominal level is the weakest level of measurement
where numbers or symbols are used simply for
categorizing subjects into different groups. The
categories must be distinct, non-overlapping and
exhaustive
•Examples: Sex M-Male F-Female
• Marital status 1-Single 2-Married 3-Widowed 4-Separated

17. Levels of Measurement
•Interval Level – is that which has the properties of the
nominal and ordinal levels, and in addition, the
distances between any two numbers on the scale are
of known sizes. An interval scale must have a
common and constant unit of measurement.
Furthermore, the unit of measurement is arbitrary
and there is no “true zero” point.
•Examples:
• IQ
• Test Result

18. Levels of Measurement
•4. Ratio Level - measurement contains all the
properties of the interval level, and in addition, it has
a “true zero” point. This is the strongest level of
measurement.
•Examples:
• Daily Allowance
• Weight (in kg)
• Age (in years)
• Number of correct answers in an exam

19. Let’s try this
•I. In the following situations, let’s determine the
population, sample, parameter and statistic.
•1. In order to estimate the true proportion of students at
a certain college who smoke cigarettes, the
administration polled a sample of 200 students and
determined that the proportion of students from the
sample who smoke cigarettes is 0.12.
• Identify the
• a) variable, b) population,
• c) sample, d) parameter, and e) statistic.

20. Let’s try this
•Solution:
•a. Variable: Whether or not a student smoke
•b. Population: The set of students at a certain college.
•c. Sample: The set of 200 students who were
interviewed.
•d. Parameter: The population proportion of students in a
certain college who smoke cigarettes.
•e. Statistic: (0.12) the proportion of students in the
sample who smoke cigarettes.

21. Let’s try this
• 2. A politician who is running for the office of mayor of a city with
25,000 registered voters commissions on a survey. In the survey,
48% of the 200 registered voters interviewed say they plan to vote
for her.
• Solution:
a. Variable: Whether or not a voter will vote the running political for
Mayor
b. Population: The group of 25,000 registered voters
c. Sample: The group of 200 registered voters who were interviewed
d. Parameter: The percentage of registered voters in the population
who plan to vote for her.
e. Statistic: (48%) The percentage of registered voters in the sample
who plan to vote for her.

22. Let’s try this
• II. Let’s determine whether the following statements belong to
the field of descriptive statistics or inferential statistics.
• 1. A badminton player wants to know his average score for the past 10
games.
• Solution: Descriptive statistics (Data is only gathered and summarized)
• 2. Janine wants to determine the variability of her six exam scores in
algebra.
• Solution: Descriptive statistics (Data is only gathered and summarized)
• 3. Based on last year’s electricity bills, Mrs. Venegas would like to forecast
the average monthly electricity bill she will pay for the next year based on
her average monthly bill in the past year.
• Solution: Inferential statistics (Data is analyzed to make a
forecast)

23. Let’s try this
• III. Let’s classify the following by a) type of variable and b) level of
measurement. If the variable is quantitative, determine whether
it is discrete or continuous.
Types of Variable Level of Measurement
Example: Degree Program (AB Social Science, AB English
Language, BS Statistics)
Qualitative Nominal
Example: Weight of women (in kg) before they took the
diet
Quantitative,
Continuous
Ratio
1. Height (in inches)
2. Sizes of shirts (i.e. XS, S, M, L, XL)
3. Zipcode (i.e. 6111 – Kabankalan)
4. Civil Status
5. Number of siblings

24. Let’s try this
• III. Let’s classify the following by a) type of variable and b) level of
measurement. If the variable is quantitative, determine whether
it is discrete or continuous.
•Solution:
• 1) Quantitative, Continuous, Ratio
• 2) Qualitative, Ordinal
• 3) Qualitative, Nominal
• 4) Qualitative, Nominal
• 5) Quantitative, Discrete, Ratio

25. Let’s Try Some More
•I. In the following situation, let’s determine the
variable, population, sample, parameter and
statistic.
•Mr. Donaldo Chan, a candidate for Vice Mayor in Orion,
Bataan wants to find out if there is a need to intensify his
campaign efforts against his opponents. He requested
the services of a group of students to interview 1,000 of
the 3,000 registered voters of Orion, Bataan. The survey
results showed that 75% of the 1,000 voters in the
sample will vote for him as vice-mayor. Identify the
following.

26. Let’s Try Some More
•I. In the following situation, let’s determine the
variable, population, sample, parameter and
statistic.
a. Variable: Whether or not a voter will vote for Mr. Chan as Vice Mayor
b. Population: The collection of 3,000 registered voters of Orion, Batangas
c. Sample: The collection of 1,000 registered voters of Orion, Batangas
d. Parameter: The percentage of registered voters in the population who
voted for Mr. Chan as Vice-Mayor
e. Statistic: The percentage of registered voters in the sample who voted
for Mr. Chan as Vice-Mayor

27. Let’s Try Some More
•II. Let’s determine whether the following statements
belong to the field of descriptive statistics or inferential
statistics.
a. A car manufacturer wishes to estimate the average lifetime of batteries by testing a
sample of 50 batteries. Answer: _________
b. A shipping company wishes to estimate the number of passengers traveling via their
ships next year using their data on the number of passengers in the past three years.
Answer: __________________
c. A marketing research group wishes to determine the number of families not eating
three times a day in the sample used for their survey. Answer: ________________
d. A politician wants to determine the total number of votes his rival obtained in the past
election based on his copies of the tally sheet of electoral returns Answer: __________
e. A politician wants to determine the total number of votes his rival obtained in the
sample used in the exit poll. Answer: _________________

28. Let’s Try Some More
•III. Let’s classify the following by a) type of variable and b)
level of measurement. If the variable is quantitative,
determine whether it is discrete or continuous.
Type of Variable Level of Measurement
Example: Weight of women (in kg) before they took the
diet
Quantitative, Continuous Ratio
1. Score in a ten-item quiz
2. Teacher’s performance rating (Excellent, Very Good,
Good, Satisfactory, Needs Improvement)
3. Total kilos of papaya harvests
4. Brand of cellphone
5. Body Temperature (in Celsius)

29. End of this topic