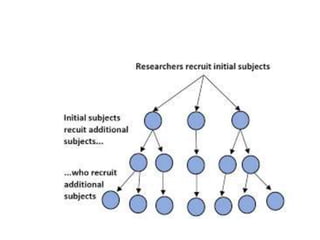
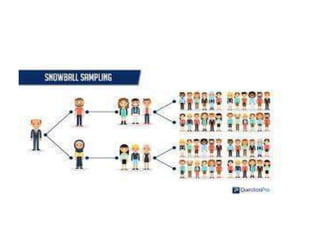
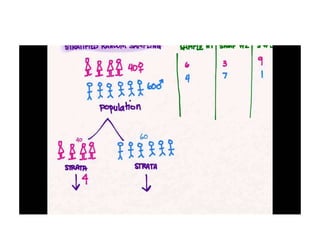
This document discusses different sampling techniques used in medical studies and research. It begins by explaining that sampling is necessary when not every member of a population can be included in a study. Some key points made about sampling include: - Samples should be sufficiently large and representative of the overall population. - Parameters describe values for the entire population, while statistics describe values calculated from a sample. - The main objectives of sampling are to estimate population parameters from sample statistics and to test hypotheses about the population. 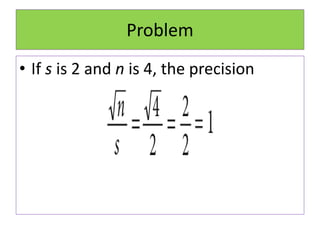- Sample size, sampling technique, and sample representativeness impact the precision and validity of conclusions drawn about the population.

1. Sampling

2. • It is not possible to include each member
(sampling unit) of the population in an
experimental study
Example
A daily life example is that of cooking rice. A
housewife just picks up a few grains of rice from
the cooking vessel and gets a fairly good idea
whether the entire lot of rice is fully cooked or it
requires more cooking.
Sampling

3. In medical studies, the sampling
data are collected from a
population or universe sufficiently
large and representative of the
population under study. Chosen by
a standard sampling technique.
Sampling

4. Parameter
A value calculated from a
defined population, such as
mean (μ), standard deviation
(σ), or standard error of mean
(1X—) is called a parameter.

5. • It is a constant value because it
covers all the members of the
population.
• A value calculated from a sample
is called a statistic.
Parameter & statistics

6. The two main objectives of sampling
are:
1. Estimation of population
parameters (mean,
proportion, etc.) from the
sample statistics.

7. 2. To test the hypothesis
about the population
from which the sample or
samples are drawn.
The two main objectives of sampling
are:

8. CHARACTERISTICS of sample
• Sample is any part of the
population.
• Large number of samples may
be taken from the same
population, still all members
may not be covered.

9. • Inferences or conclusions drawn
from the sample are applied to
the whole population or universe
• but it is generalized or valid, only
if the sample is sufficiently large
and unbiased.
CHARACTERISTICS of sample

10. A representative sample will
have its statistics almost
equal to the parameters of
the entire population.
CHARACTERISTICS of sample

11. Sample size
• Precision depends on the sample
size.
• Sample size should not be less than
30.
• A sample, small in size, is a biased
one and should never be depended
upon for drawing any conclusion.

12. • The size of sample is very vital
in any scientific study.
• A sample of size greater than
30 is considered large enough
for statistical purposes. A small
sample lacks precision.
Sample size

13. Precision formulae
Precision =
• S is standard deviation.
• n = square root of sample size

14. Problem
• If s is 2 and n is 4, the precision

15. For quantitative data
Mean pulse rate of a population is believed to be 70 per minute with a
standard deviation of 8 beats. Calculate the minimum size of the sample to
verify this, if allowable error E = ±1 beat at 5% risk.

16. For qualitative data
Incidence rate in the last influenza epidemic
was found to be 50 per thousand (5%) of the
population exposed. What should be the size
of sample to find incidence rate in the current
epidemic if allowable error is 0.005 and 0.01?

17. • If E = 0.005
If E = 0.01 So

18. SAMPLING TECHNIQUES

20. Simple Random Sampling
The method is applicable when the population is
• Small.
• Homogeneous and
• Readily available
[such as patients coming to hospital or lying in
the wards.]

21. Simple Random Sampling-unrestricted
random sampling’.
• It is used in experimental medicine or clinical
trials like testing the efficacy of a particular
drug.
To ensure randomness of selection, one may
adopt either
• Lottery method or
• Refer to table of random numbers.

23. Lottery method
• Suppose, 10 patients are to be put on a trial out of the
100 available, Note the serial number of patients on
100 cards and shuffle them well.
• Draw out one and note the number. Replace the card
drawn, reshuffle and draw the second card. Repeat the
process till 10 numbers are drawn.
• Reject the cards that are drawn for second time.
• The 10 cards drawn thus will indicate the patient’s
number to be put on trial and the 10 patients selected
in this manner form the random sample.
• Similar procedure may be followed for selecting the
control if need be. This is sampling with replacement.

24. Table of random number method
• The other common method of drawing the sample is
by making use of the published tables of random
numbers.
• First give serial numbers to all the 100 patients in the
above example at random, starting from any patient.
• This reduces the bias at the very start.
• Number higher than 100 could be rejected too.
• Making use of the rows below. Thus, 10 numbers for
the sample are chosen.
• We can start from any row or column or even
diagonally.

26. Systematic Sampling
• This method is popularly used in those cases
when a complete list of population from which
sample is to be drawn, is available.
• It is more often applied to field studies when the
population is large, scattered and not
homogeneous.
• Systematic procedure is followed to choose a
sample by taking every Kth house or patient
where K refers to the sample interval, which is
calculated by the formula:

27. if 10% sample is to be taken out of one
thousand patients.

29. Stratified Sampling
• This method is followed when the population
is not homogeneous.
• The population under study is first divided
into homogeneous groups or classes called
strata and the sample is drawn from each
stratum at random in proportion to its size.

30. It is a method of sampling for giving
representation to all strata of society or
population such as selecting sample from
defined areas, classes, ages, sexes, etc.
This technique gives more representative
sample than simple random sampling in a given
large population.

33. Multistage Sampling
• This method refers to the sampling procedures
carried out several stages using random sampling
techniques.
• This is employed in large country surveys.
• In the first stage, random numbers of districts
are chosen in all the states, followed by random
numbers of talukas, villages and units,
respectively, e.g. for hookworm survey in a
district, choose 10% villages in the talukas and
then examine stools of all persons in every 10th
house.

34. Multistage Sampling

36. Cluster Sampling
• A cluster is a randomly selected group.
• This method is used when units of population are
natural groups or clusters such as villages, wards,
blocks, slums of a town, factories, work-shops or
children of a school, etc.
• Fortunately, the technique of cluster sampling
allows small number of the target population to
be sampled while the data provided is statistically
valid at 95% confidence limits (10% variation).

38. • From the chosen clusters, 30 in number, the
entire population is surveyed. Cluster
sampling gives a higher standard error but the
data collection in this method is simpler and
involves less time and cost than in other
sampling techniques.
Cluster Sampling

39. Identification of clusters of collection
of data
• List all cities, towns, villages and wards of
cities with their population falling in the target
area under study for evaluation.
• Calculate cumulative population and divide
the same by 30. This gives the sampling
interval.
• Select a random number less than or equal to
sampling interval having same number of
digits. This forms the first cluster.

40. Identification of clusters of collection
of data
• Random number plus sampling interval. Gives
the population of 2nd cluster.
• Second cluster + sampling interval = 3rd
cluster.
3rd cluster + sampling interval = 4th cluster
and so on. Last or 30th cluster = 29th cluster+
sampling interval.
• All houses with population are numbered.

41. Multiphase Sampling
• In this method, part of the information is
collected from the whole sample and part from
the subsample.
• In a tuberculosis survey, physical examination or
Mantoux test may be done in all cases of the
sample in the first phase; in the second phase X-
ray of the chest may be done in Mantoux positive
cases and in those with clinical symptoms, while
sputum may be examined in X-ray positive cases
in the third phase only.

42. • Number in the subsamples in 2nd and 3rd
phase will become successively smaller and
smaller. Survey by such procedure will be less
costly, less laborious and more purposeful.
• Sometime two or more independent samples
may be taken by different survey teams to
compare the results. Such samples may
overlap to some extent or be exclusive of each
other.

44. Non –Probability sampling
• It does not provide every component in the
population or universe with an equal chance
being included in the sample.
• The researcher may select a sample which
may get results favorable to him.
• Sampling error cannot be estimated.

45. Purposive or Judgmental sampling
• Deliberate sampling.
• Choice of sample items depends primarily on
the judgement of the investigator.
• The investigator includes those elements in
the sample with regard to the characteristics
of research topics.
• In this method Researcher has complete
freedom to choose his sample according to his
wishes and desires.

46. Purposive or Judgmental sampling

47. Purposive or Judgmental sampling

48. Advantage
• Simple and economical
• Practical method when randomization is not
possible.
• Helped in solving many economic and
business problems.
• Knowledge of the researcher can be best used
in this method of sampling.

49. Disadvantage
• Sampling is not free from error.
• It includes uncontrolled variation.
• Sample may be biased because
researcher can select sample as per
his wish and desire.

50. Convenience / Accidental sampling
• It is also known as haphazard / incidental
sampling.
• Investigator studies all those persons who are
conveniently available or who accidentally come
in his contact during investigation.
• It is common among market research and
newspaper reporters.
• During election period media personnel often
present man on the street interviews that are
presumed to reflect public opinion.

51. Convenience / Accidental sampling

52. Advantage
• Sampling is quick, easy and economical
method.
• It is used frequently in behavioral sciences and
exploratory research.

53. Disadvantage
• It is not free from error.
• Parametric statistics cannot be used.
• It is not a representative of the population
• it may be a very biased sample.

54. Quota sampling
• Non random form of stratified sampling
method.
• The universe is divided into strata on the basis
of certain characteristics.
• quota is fixed for each stratum in proportion
to its size.
• It is the most commonly used method of
sampling in market survey, opinion polls and
municipal surveys.

55. For studying the attitudes of persons
towards use of loudspeaker in religious
place with 1000 males and 500
females belonging to different religion
• Quota can be fixed
• The ratio of one female for every two
males.
• On the basis of number of persons in
each of the three religious groups such as
Hindu, Muslim, or others.

56. Advantage
• Simple and most frequently used
in social survey.
• Less costly than other techniques.
• Completed in very short period of
time.

57. Dis advantage
• It is not a true representative of total
sample population.
• Not possible to estimate sampling error.
• It has interviewers bias in the selection.
• It has the influence of regional
geographical and social factors.

58. Snow ball sampling
• The process of selecting a sample using networks.
• The investigator starts the research with the few
respondents who are known to him.
• The respondents give other names who meet the
criteria of research, who in turn give more
names.
• This process of sample selection is continued
until adequate number of person is interviewed.

61. Advantage
• In this manner, the investigator accumulates
more and more respondents.
• It will be useful when you don’t have the idea
about group or organization under study.
• Less cost
• Less sample size.

62. Disadvantage
• It is difficult to use when sample becomes
fairly large.
• The choice of the entire sample depends upon
the choice of individuals at the first stage.
• If they belong to a particular faction the study
may be biased.
• Serious problem if there is a major difference
between those who are widely known by
others and those who are not.