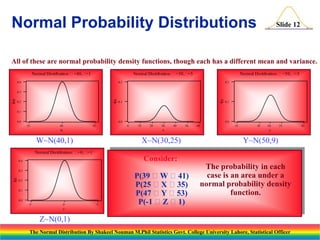
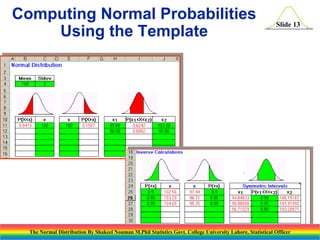
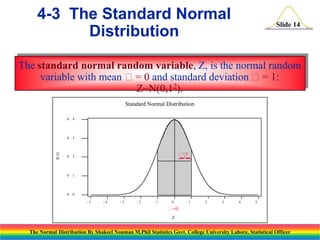
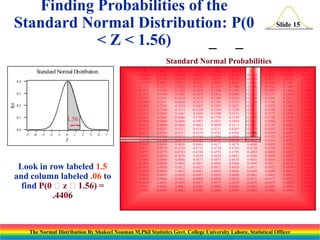
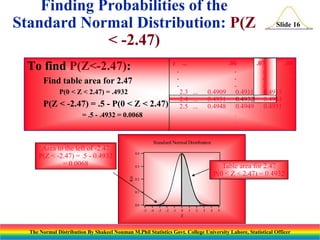
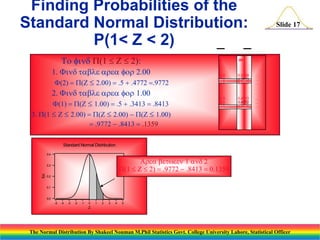
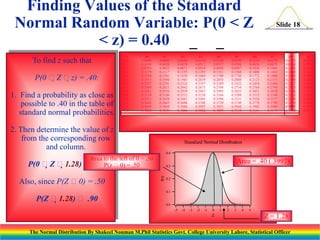
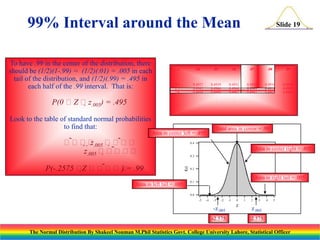
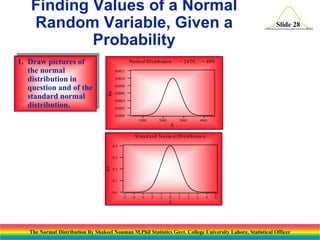
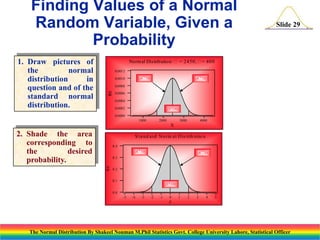
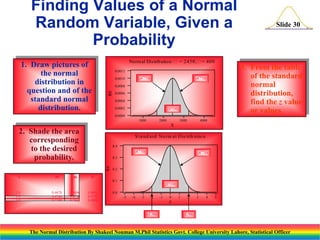
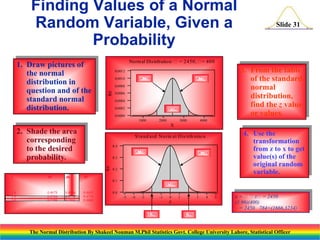
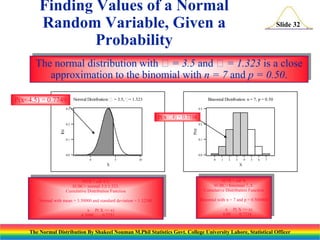
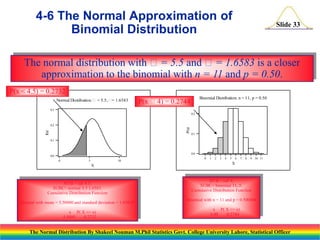
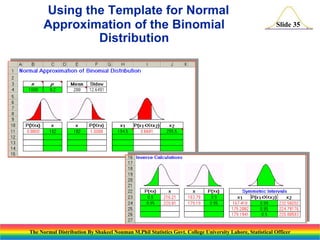
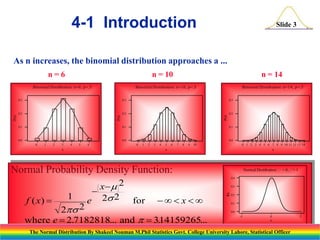
The document discusses the normal distribution and its key properties. It introduces the normal probability density function and how it is characterized by a mean and variance. Some key properties covered are that the sum of independent normally distributed variables is also normally distributed, with the mean being the sum of the individual means and the variance being the sum of the individual variances. It also discusses how to compute probabilities and find values for the standard normal distribution.

1. The Normal Distribution
Slide 1
Shakeel Nouman
M.Phil Statistics
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

2. 4







Slide 2
The Normal Distribution
Using Statistics
The Normal Probability Distribution
The Standard Normal Distribution
The Transformation of Normal Random
Variables
The Inverse Transformation
The Normal Distribution as an
Approximation to Other Probability
Distributions
Summary and Review of Terms
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

3. 4-1 Introduction
Slide 3
As n increases, the binomial distribution approaches a ...
n=6
n = 10
Bino mial Dis trib utio n: n=6, p =.5
n = 14
Bino mial Distrib utio n: n=1 0 , p =.5
Bino mial Dis trib utio n: n=1 4 , p =.5
0.3
0.2
0.2
0.2
0.1
P(x)
0.3
P(x)
P(x)
0.3
0.1
0.0
0.1
0.0
0
1
2
3
4
5
6
0.0
0
1
x
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
x
x
Normal Probability Density Function:
f ( x) 
1




 x
2
2p
where e  2.7182818... and p  314159265...
.
0.4
0.3
f(x)
x  2

e 2 2 for





Normal Distribution:  = 0,= 1
0.2
0.1
0.0
-5
0
x
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
5

4. The Normal Probability
Distribution
Slide 4
The normal probability density function:
1
e
0.4
x  2




2 2
0.3
for
 x
2p 2
where e  2.7182818... and p  314159265...
.
f(x)
f ( x) 






Normal Dis tribution:  = 0,= 1
0.2
0.1
0.0
-5
0
x
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
5

5. Properties of the Normal
Probability Distribution
•
Slide 5
The normal is a family of
Bell-shaped and symmetric distributions. because the
distribution is symmetric, one-half (.50 or 50%) lies
on either side of the mean.
Each is characterized by a different pair of mean, ,


and variance,  . That is: [X~N( )].
Each is asymptotic to the horizontal axis.
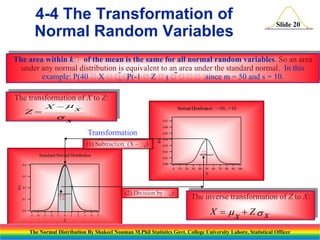
The area under any normal probability density
function within kof is the same for any normal
distribution, regardless of the mean and variance.
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

6. Properties of the Normal
Probability Distribution (continued)
•
•
•
Slide 6
If several independent random variables are normally
distributed then their sum will also be normally
distributed.
The mean of the sum will be the sum of all the
individual means.
The variance of the sum will be the sum of all the
individual variances (by virtue of the independence).
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

7. Properties of the Normal
Probability Distribution
(continued)
•
•
•
•
Slide 7
If X1, X2, …, Xn are independent normal random
variable, then their sum S will also be normally
distributed with
E(S) = E(X1) + E(X2) + … + E(Xn)
V(S) = V(X1) + V(X2) + … + V(Xn)
Note: It is the variances that can be added above and
not the standard deviations.
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

8. Properties of the Normal
Probability Distribution – Example
4-1
Slide 8
Example 4.1: Let X1, X2, and X3 be independent random
variables that are normally distributed with means and
variances as shown.
Mean
Variance
X1
10
1
X2
20
2
X3
30
3
Let S = X1 + X2 + X3. Then E(S) = 10 + 20 + 30 = 60 and
V(S) = 1 + 2 + 3 = 6. The standard deviation of S 6
is
= 2.45.
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

9. Properties
of
the
Normal
Probability Distribution (continued)
•
•
•
•
Slide 9
If X1, X2, …, Xn are independent normal random
variable, then the random variable Q defined as Q =
a1X1 + a2X2 + … + anXn + b will also be normally
distributed with
E(Q) = a1E(X1) + a2E(X2) + … + anE(Xn) + b
V(Q) = a12 V(X1) + a22 V(X2) + … + an2 V(Xn)
Note: It is the variances that can be added above and
not the standard deviations.
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

10. Properties of the Normal
Probability Distribution – Example
4-3
Slide 10
Example 4.3: Let X1 , X2 , X3 and X4 be independent random variables
that are normally distributed with means and variances as shown.
Find the mean and variance of Q = X1 - 2X2 + 3X2 - 4X4 + 5
Mean
Variance
X1
12
4
X2
-5
2
X3
8
5
X4
10
1
E(Q) = 12 – 2(-5) + 3(8) – 4(10) + 5 = 11
V(Q) = 4 + (-2)2(2) + 32(5) + (-4)2(1) = 73
SD(Q) =
73  8.544
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

11. Computing the Mean, VarianceSlide 11
and Standard Deviation for the
Sum of Independent Random
Variables Using the Template
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

12. Normal Probability Distributions
Slide 12
All of these are normal probability density functions, though each has a different mean and variance.
Normal Distribution: =40, 
=1
Normal Distribution: =30, 
=5
0.4
Normal Distribution: =50, 
=3
0.2
0.2
0.2
f(y)
f(x)
f(w)
0.3
0.1
0.1
0.1
0.0
0.0
35
40
45
0.0
0
w
10
20
30
40
50
x
W~N(40,1)
X~N(30,25)
60
35
45
50
55
y
Y~N(50,9)
Normal Distribution:  
=0, =1
Consider:
0.4
f(z)
0.3
0.2
0.1
0.0
-5
0
5
P(39 W 41)
P(25 X 35)
P(47 Y 53)
P(-1 Z 1)
The probability in each
case is an area under a
normal probability density
function.
z
Z~N(0,1)
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
65

13. Computing Normal Probabilities
Using the Template
Slide 13
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

14. 4-3 The Standard Normal
Distribution
Slide 14
The standard normal random variable, Z, is the normal random
variable with mean = 0 and standard deviation = 1:
Z~N(0,12).
Standard Normal Distribution
0 .4

=1
{
f( z)
0 .3
0 .2
0 .1
0 .0
-5
-4
-3
-2
-1
0
1
2
3
4
5

=0
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

15. Finding Probabilities of the
Standard Normal Distribution: P(0
< Z < 1.56)
Slide 15
Standard Normal Probabilities
Standard Normal Distribution
0.4
f(z)
0.3
0.2
0.1
{
1.56
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
Look in row labeled 1.5
and column labeled .06 to
find P(0 z 1.56) =
.4406
z
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
.00
0.0000
0.0398
0.0793
0.1179
0.1554
0.1915
0.2257
0.2580
0.2881
0.3159
0.3413
0.3643
0.3849
0.4032
0.4192
0.4332
0.4452
0.4554
0.4641
0.4713
0.4772
0.4821
0.4861
0.4893
0.4918
0.4938
0.4953
0.4965
0.4974
0.4981
0.4987
.01
0.0040
0.0438
0.0832
0.1217
0.1591
0.1950
0.2291
0.2611
0.2910
0.3186
0.3438
0.3665
0.3869
0.4049
0.4207
0.4345
0.4463
0.4564
0.4649
0.4719
0.4778
0.4826
0.4864
0.4896
0.4920
0.4940
0.4955
0.4966
0.4975
0.4982
0.4987
.02
0.0080
0.0478
0.0871
0.1255
0.1628
0.1985
0.2324
0.2642
0.2939
0.3212
0.3461
0.3686
0.3888
0.4066
0.4222
0.4357
0.4474
0.4573
0.4656
0.4726
0.4783
0.4830
0.4868
0.4898
0.4922
0.4941
0.4956
0.4967
0.4976
0.4982
0.4987
.03
0.0120
0.0517
0.0910
0.1293
0.1664
0.2019
0.2357
0.2673
0.2967
0.3238
0.3485
0.3708
0.3907
0.4082
0.4236
0.4370
0.4484
0.4582
0.4664
0.4732
0.4788
0.4834
0.4871
0.4901
0.4925
0.4943
0.4957
0.4968
0.4977
0.4983
0.4988
.04
0.0160
0.0557
0.0948
0.1331
0.1700
0.2054
0.2389
0.2704
0.2995
0.3264
0.3508
0.3729
0.3925
0.4099
0.4251
0.4382
0.4495
0.4591
0.4671
0.4738
0.4793
0.4838
0.4875
0.4904
0.4927
0.4945
0.4959
0.4969
0.4977
0.4984
0.4988
.05
0.0199
0.0596
0.0987
0.1368
0.1736
0.2088
0.2422
0.2734
0.3023
0.3289
0.3531
0.3749
0.3944
0.4115
0.4265
0.4394
0.4505
0.4599
0.4678
0.4744
0.4798
0.4842
0.4878
0.4906
0.4929
0.4946
0.4960
0.4970
0.4978
0.4984
0.4989
.06
0.0239
0.0636
0.1026
0.1406
0.1772
0.2123
0.2454
0.2764
0.3051
0.3315
0.3554
0.3770
0.3962
0.4131
0.4279
0.4406
0.4515
0.4608
0.4686
0.4750
0.4803
0.4846
0.4881
0.4909
0.4931
0.4948
0.4961
0.4971
0.4979
0.4985
0.4989
.07
0.0279
0.0675
0.1064
0.1443
0.1808
0.2157
0.2486
0.2794
0.3078
0.3340
0.3577
0.3790
0.3980
0.4147
0.4292
0.4418
0.4525
0.4616
0.4693
0.4756
0.4808
0.4850
0.4884
0.4911
0.4932
0.4949
0.4962
0.4972
0.4979
0.4985
0.4989
.08
0.0319
0.0714
0.1103
0.1480
0.1844
0.2190
0.2517
0.2823
0.3106
0.3365
0.3599
0.3810
0.3997
0.4162
0.4306
0.4429
0.4535
0.4625
0.4699
0.4761
0.4812
0.4854
0.4887
0.4913
0.4934
0.4951
0.4963
0.4973
0.4980
0.4986
0.4990
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
.09
0.0359
0.0753
0.1141
0.1517
0.1879
0.2224
0.2549
0.2852
0.3133
0.3389
0.3621
0.3830
0.4015
0.4177
0.4319
0.4441
0.4545
0.4633
0.4706
0.4767
0.4817
0.4857
0.4890
0.4916
0.4936
0.4952
0.4964
0.4974
0.4981
0.4986
0.4990

16. Finding Probabilities of the
Standard Normal Distribution: P(Z
< -2.47)
To find P(Z<-2.47):
Find table area for 2.47
P(0 < Z < 2.47) = .4932
P(Z < -2.47) = .5 - P(0 < Z < 2.47)
z ...
.
.
.
2.3 ...
2.4 ...
2.5 ...
Slide 16
.06
.07
.08
.
.
.
.
.
.
.
.
.
0.4909 0.4911 0.4913
0.4931 0.4932 0.4934
0.4948 0.4949 0.4951
.
.
.
= .5 - .4932 = 0.0068
Standard Normal Distribution
Area to the left of -2.47
P(Z < -2.47) = .5 - 0.4932
= 0.0068
0.4
Table area for 2.47
P(0 < Z < 2.47) = 0.4932
f(z)
0.3
0.2
0.1
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

17. Finding Probabilities of the
Standard Normal Distribution:
P(1< Z < 2)
To find P(1  Z  2):
1. Find table area for 2.00
F(2)  P(Z  2.00)  .5 + .4772 .9772
2. Find table area for 1.00
F(1)  P(Z  1.00)  .5 + .3413  .8413
3. P(1  Z  2.00)  P(Z  2.00)  P(Z  1.00)
z
.00
.
.
.
0.9
1.0
1.1
.
.
.
1.9
2.0
2.1
 .9772  .8413  .1359
.
.
.
.
.
.
0.3159
0.3413
0.3643
.
.
.
0.4713
0.4772
0.4821
.
.
.
Slide 17
...
...
...
...
...
...
...
Standard Normal Distribution
0.4
Area between 1 and 2
P(1  Z  2)  .9772  .8413  0.1359
f(z)
0.3
0.2
0.1
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

18. Finding Values of the Standard
Normal Random Variable: P(0 < Z
< z) = 0.40
To find z such that
P(0 Z z) = .40:
1. Find a probability as close as
possible to .40 in the table of
standard normal probabilities.
z
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
.
.
.
.00
0.0000
0.0398
0.0793
0.1179
0.1554
0.1915
0.2257
0.2580
0.2881
0.3159
0.3413
0.3643
0.3849
0.4032
.
.
.
.01
0.0040
0.0438
0.0832
0.1217
0.1591
0.1950
0.2291
0.2611
0.2910
0.3186
0.3438
0.3665
0.3869
0.4049
.
.
.
.02
0.0080
0.0478
0.0871
0.1255
0.1628
0.1985
0.2324
0.2642
0.2939
0.3212
0.3461
0.3686
0.3888
0.4066
.
.
.
2. Then determine the value of z
from the corresponding row
and column.
.03
0.0120
0.0517
0.0910
0.1293
0.1664
0.2019
0.2357
0.2673
0.2967
0.3238
0.3485
0.3708
0.3907
0.4082
.
.
.
.04
0.0160
0.0557
0.0948
0.1331
0.1700
0.2054
0.2389
0.2704
0.2995
0.3264
0.3508
0.3729
0.3925
0.4099
.
.
.
.05
0.0199
0.0596
0.0987
0.1368
0.1736
0.2088
0.2422
0.2734
0.3023
0.3289
0.3531
0.3749
0.3944
0.4115
.
.
.
.06
0.0239
0.0636
0.1026
0.1406
0.1772
0.2123
0.2454
0.2764
0.3051
0.3315
0.3554
0.3770
0.3962
0.4131
.
.
.
Slide 18
.07
0.0279
0.0675
0.1064
0.1443
0.1808
0.2157
0.2486
0.2794
0.3078
0.3340
0.3577
0.3790
0.3980
0.4147
.
.
.
.08
0.0319
0.0714
0.1103
0.1480
0.1844
0.2190
0.2517
0.2823
0.3106
0.3365
0.3599
0.3810
0.3997
0.4162
.
.
.
Standard Normal Distribution
0.4
Area to the left of 0 = .50
P(0 Z 1.28)  .40P(z 0) = .50
f(z)
Also, since P(Z 0) = .50
Area = .40 (.3997)
0.3
0.2
0.1
P(Z 1.28)  .90
0.0
-5
-4
-3
-2
-1
0
Z
1
2
3
4
5
Z = 1.28
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
.09
0.0359
0.0753
0.1141
0.1517
0.1879
0.2224
0.2549
0.2852
0.3133
0.3389
0.3621
0.3830
0.4015
0.4177
.
.
.

19. 99% Interval around the Mean
To have .99 in the center of the distribution, there
should be (1/2)(1-.99) = (1/2)(.01) = .005 in each
tail of the distribution, and (1/2)(.99) = .495 in
each half of the .99 interval. That is:
P(0 Z z.005) = .495
z
.04
.
.
.
.
2.4 ...
2.5 ...
2.6 ...
.
.
.
.05
.08
.
.
.
0.4931
0.4948
0.4961
.
.
.
.09
.
.
.
0.4932
0.4949
0.4962
.
.
.
.
.
.
0.4934
0.4951
0.4963
.
.
.
.
.
0.4936
0.4952
0.4964
.
.
.
Total area in center = .99
Area in center left = .495
0.4
Area in center right = .495
0.3
f(z)
P(-.2575   .99
Z
)=
.07
.
.
.
0.4929
0.4946
0.4960
.
.
.
Look to the table of standard normal probabilities
to find that:
  
z.005
z.005 
.06
.
.
.
0.4927
0.4945
0.4959
.
.
.
Slide 19
0.2
Area in right tail = .005
Area in left tail = .005
0.1
0.0
-5
-4
-3
-2
-z.005
-2.575
-1
0
Z
1
2
3
4
5
z.005
2.575
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

20. 4-4 The Transformation of
Normal Random Variables
Slide 20
The area within k of the mean is the same for all normal random variables. So an area
under any normal distribution is equivalent to an area under the standard normal. In this
example: P(40 X 
P(-1 Z  
since m = 50 and s = 10.
The transformation of X to Z:
X x
Z
x
Normal Distribution:=50,
=10
0.07
0.06
Transformation
f(x)
(1) Subtraction: (X -  )
x
0.05
0.04
0.03
 10
=
{
0.02
Standard Normal Distribution
0.01
0.00
0.4
0
20
30
40
50
60
70
80
90 100
X
0.3
0.2
(2) Division by  )
x
{
f(z)
10
1.0
0.1
0.0
-5
-4
-3
-2
-1
0
Z
1
2
3
4
5
The inverse transformation of Z to X:
X  x + Z x
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

21. Using the Normal
Transformation
Example 4-9
X~N(160,302)
Slide 21
Example 4-10
X~N(127,222)
P (100  X  180)
 100    X    180   
 P

P ( X  150)
 X    150   
 P



 

 
 100  160  Z  180  160
P

 30
30 
(
)
 P 2  Z  .6667
 0.4772 + 0.2475  0.7247
 
 
 150  127 
P Z 


22 
(
)
 P Z  1.045
 0.5 + 0.3520  0.8520
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

22. Using the Normal
Transformation - Example 4-11
Normal Dis tribution:  = 383, = 12
Example 4-11
X~N(383,122)
0.05
0.04
(
 
399  383
)
12
 P 0.9166  Z  1.333
 0.4088  0.3203  0.0885


0.03
0.02
0.01
Standard Normal Distribution
0.00
340
0.4
390
X
0.3
f(z)

f( )
X
P ( 394  X  399)
 394   X   399   
 P



 

 394  383
P
Z 
 12
Slide 22
0.2
0.1
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
Template solution
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
440

23. The Transformation of Normal
Random Variables
The transformation of X to Z:
Z 
X  x
x
Slide 23
The inverse transformation of Z to X:
X  
+ Z
x
x
The transformation of X to Z, where a and b are numbers::
a  

P( X  a)  P Z 


 
b  

P( X  b)  P Z 


 
b  
a 
P(a  X  b)  P
Z

 
 
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

24. Normal
Rule)
Probabilities
(Empirical
S t a n d a rd N o rm a l D is trib u tio n
• The probability that a normal
•
•
0 .4
0 .3
f(z)
random variable will be within 1
standard deviation from its mean
(on either side) is 0.6826, or
approximately 0.68.
The probability that a normal
random variable will be within 2
standard deviations from its mean
is 0.9544, or approximately 0.95.
The probability that a normal
random variable will be within 3
standard deviation from its mean is
0.9974.
Slide 24
0 .2
0 .1
0 .0
-5
-4
-3
-2
-1
0
1
2
3
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
4
5

25. 4-5 The Inverse Transformation
Slide 25
The area within k of the mean is the same for all normal random variables. To find a
probability associated with any interval of values for any normal random variable, all that
is needed is to express the interval in terms of numbers of standard deviations from the
mean. That is the purpose of the standard normal transformation. If X~N(50,102),
70  50 
 x   70   

P( X  70)  P

  P Z 
  P( Z  2)
 

 
10 
That is, P(X >70) can be found easily because 70 is 2 standard deviations above the mean
of X: 70 = + 2 P(X > 70) is equivalent to P(Z > 2), an area under the standard normal
.
distribution.
Normal Distribution:  = 124, = 12
Example 4-12
X~N(124,122)
P(X > x) = 0.10 and P(Z > 1.28) 
0.10
x = + z= 124 + (1.28)(12) =
139.36
.
.
.
1.1
1.2
1.3
.
.
.
.07
.
.
.
0.3790
0.3980
0.4147
.
.
.
...
...
...
.
.
.
.
.
.
.08
.
.
.
0.3810
0.3997
0.4162
.
.
.
.09
.
.
.
0.3830
0.4015
0.4177
.
.
.
0.03
f(x)
z
0.04
0.02
0.01
0.01
0.00
80
130
X
139.36
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer
180

26. Template Solution for Example
4-12
Slide 26
Example 4-12
X~N(124,122)
P(X > x) = 0.10 and P(Z > 1.28) 
0.10
x = + z= 124 + (1.28)(12) =
139.36
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

27. The Inverse Transformation
(Continued)
Example 4-13
X~N(5.7,0.52)
P(X > x)=0.01 and P(Z > 2.33) 
0.01
x = + z= 5.7 + (2.33)(0.5) = 6.865
z
.
.
.
2.2
2.3
2.4
.
.
.
.02
.
.
.
0.4868
0.4898
0.4922
.
.
.
...
...
...
.
.
.
.03
.
.
.
0.4871
0.4901
0.4925
.
.
.
.
.
.
Example 4-14
X~N(2450,4002)
P(a<X<b)=0.95 and P(-1.96<Z<1.96)
0.95
x = z= 2450 (1.96)(400) = 2450
784=(1666,3234)
P(1666 < X < 3234) = 0.95
.04
.
.
.
0.4875
0.4904
0.4927
z
.
.
.
1.8
1.9
2.0
.
.
.
.
Normal Distribution: = 5.7  0.5
=
...
...
...
.
.
.06
.
.
.
0.4686
0.4750
0.4803
.
.
.
0.0015
Area = 0.49
.4750
.4750
0.0010
f(x)
0.5
0.4
X.01 = 
+z= 5.7 + (2.33)(0.5) = 6.865
0.3
0.0005
0.2
.0250
.0250
Area = 0.01
0.1
0.0
0.0000
3.2
4.2
5.2
6.2
7.2
8.2
1000
2000
X
-5
-4
-3
-2
-1
0
z
3000
4000
X
1
2
3
4
5
Z.01 = 2.33
-5
-4
-3
-2
-1.96
-1
0
Z
1
2
3
.07
.
.
.
0.4693
0.4756
0.4808
.
.
Normal Distribution:  = 2450 = 400
0.6
f(x)
.05
.
.
.
0.4678
0.4744
0.4798
.
.
.
.
.
0.8
0.7
Slide 27
4
5
1.96
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

28. Finding Values of a Normal
Random Variable, Given a
Probability
Norm al Distribution:  = 24 50, = 40 0
0.0012
.
0.0010
.
0.0008
.
f(x)
1. Draw pictures of
the normal
distribution in
question and of the
standard normal
distribution.
Slide 28
0.0006
.
0.0004
.
0.0002
.
0.0000
1000
2000
3000
4000
X
S ta nd a rd N o rm al D is trib utio n
0.4
f(z)
0.3
0.2
0.1
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

29. Finding Values of a Normal
Random Variable, Given a
Probability
Norm al Distribution:  = 24 50, = 400
0.0012
.
.4750
0.0010
.
.4750
0.0008
.
f(x)
1. Draw pictures of
the
normal
distribution
in
question and of the
standard normal
distribution.
Slide 29
0.0006
.
0.0004
.
0.0002
.
.9500
0.0000
1000
2000
3000
4000
X
2. Shade the area
corresponding to
the
desired
probability.
S ta nd a rd No rm al D is trib utio n
0.4
.4750
.4750
f(z)
0.3
0.2
0.1
.9500
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

30. Finding Values of a Normal
Random Variable, Given a
Probability
Norm al Distribution:  = 2450, = 400
3. From the table
of the standard
normal
distribution,
find the z value
or values.
0.0012
.
.4750
0.0010
.
.4750
0.0008
.
f(x)
1. Draw pictures of
the normal
distribution in
question and of the
standard normal
distribution.
Slide 30
0.0006
.
0.0004
.
0.0002
.
.9500
0.0000
1000
2000
3000
4000
X
2. Shade the area
corresponding
to the desired
probability.
S ta nd a rd No rm al D is trib utio n
0.4
.4750
f(z)
z
.
.
.
1.8
1.9
2.0
.
.
.05
.
.
.
0.4678
0.4744
0.4798
.
.
.
.
...
...
...
.
.
.
.06
.
.
.
0.4686
0.4750
0.4803
.
.
.4750
0.3
.07
.
.
.
0.4693
0.4756
0.4808
.
0.2
0.1
.9500
0.0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Z
.
-1.96
1.96
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

31. Finding Values of a Normal
Random Variable, Given a
Probability
Norm al Distribution:  = 24 50, = 400
3. From the table
of the standard
normal
distribution,
find the z value
or values.
0.0012
.
.4750
0.0010
.
.4750
0.0008
.
f(x)
1. Draw pictures of
the normal
distribution in
question and of the
standard normal
distribution.
Slide 31
0.0006
.
0.0004
.
0.0002
.
.9500
0.0000
1000
2000
3000
4000
X
2. Shade the area
corresponding
to the desired
probability.
0.4
.4750
.
.
.
...
...
...
.
.
.05
.
.
.
0.4678
0.4744
0.4798
.
.
.06
.
.
.
0.4686
0.4750
0.4803
.
.
.4750
0.3
f(z)
z
.
.
.
1.8
1.9
2.0
.
.
4. Use the
transformation
from z to x to get
value(s) of the
original random
variable.
S ta nd a rd No rm al D is trib utio n
.07
.
.
.
0.4693
0.4756
0.4808
.
.
0.2
0.1
.9500
0.0
-5
-4
-3
-2
-1
0
1
2
Z
-1.96
3
4
5
x = z= 2450
(1.96)(400)
= 2450 784=(1666,3234)
1.96
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

32. Finding Values of a Normal
Random Variable, Given a
Probability
Slide 32
The normal distribution with = 3.5 and = 1.323 is a close
approximation to the binomial with n = 7 and p = 0.50.
P(x<4.5) = 0.7749
Normal Distribution:  = 3.5, = 1.323
Binomial Distribution: n = 7, p = 0.50
0.3
0.3
P( x  = 0.7734
4)
0.2
f(x)
P(x)
0.2
0.1
0.1
0.0
0.0
0
5
10
X
0
1
2
3
4
5
6
7
X
MTB > cdf 4.5;
SUBC> normal 3.5 1.323.
Cumulative Distribution Function
MTB > cdf 4;
SUBC> binomial 7,.5.
Cumulative Distribution Function
Normal with mean = 3.50000 and standard deviation = 1.32300
Binomial with n = 7 and p = 0.500000
x P( X <= x)
4.5000
0.7751
x P( X <= x)
4.00
0.7734
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

33. 4-6 The Normal Approximation of
Binomial Distribution
Slide 33
The normal distribution with = 5.5 and = 1.6583 is a closer
approximation to the binomial with n = 11 and p = 0.50.
P(x < 4.5) = 0.2732
Normal Distribution: = 5.5, = 1.6583
Binomial Distribution: n = 11, p = 0.50
P(x 4) = 0.2744
0.3
0.2
f(x)
P(x)
0.2
0.1
0.1
0.0
0.0
0
5
10
X
MTB > cdf 4.5;
SUBC> normal 5.5 1.6583.
Cumulative Distribution Function
Normal with mean = 5.50000 and standard deviation = 1.65830
x P( X <= x)
4.5000
0.2732
0
1
2
3
4
5
6
7
8
9 10 11
X
MTB > cdf 4;
SUBC> binomial 11,.5.
Cumulative Distribution Function
Binomial with n = 11 and p = 0.500000
x P( X <= x)
4.00
0.2744
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

34. Approximating a Binomial
Probability Using the Normal
Distribution
Slide 34
b  np 
 a  np
P ( a  X  b)  P 
Z


 np(1  p)
np(1  p) 
for n large (n  50) and p not too close to 0 or 1.00
or:
b + 0.5  np 
 a  0.5  np
P ( a  X  b)  P 
Z


np(1  p) 
 np(1  p)
for n moderately large (20  n < 50).
If p is either small (close to 0) or large (close to 1), use the Poisson
approximation.
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

35. Using the Template for Normal
Approximation of the Binomial
Distribution
Slide 35
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer

36. Slide 36
Name
Religion
Domicile
Contact #
E.Mail
M.Phil (Statistics)
Shakeel Nouman
Christian
Punjab (Lahore)
0332-4462527. 0321-9898767
sn_gcu@yahoo.com
sn_gcu@hotmail.com
GC University, .
(Degree awarded by GC University)
M.Sc (Statistics)
Statitical Officer
(BS-17)
(Economics & Marketing
Division)
GC University, .
(Degree awarded by GC University)
Livestock Production Research Institute
Bahadurnagar (Okara), Livestock & Dairy Development
Department, Govt. of Punjab
The Normal Distribution By Shakeel Nouman M.Phil Statistics Govt. College University Lahore, Statistical Officer