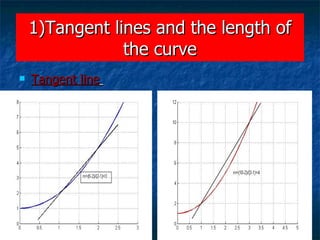
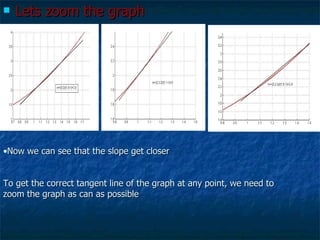
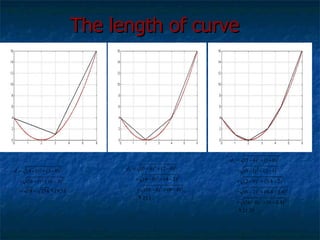
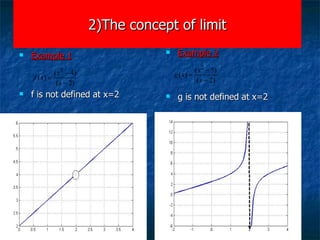
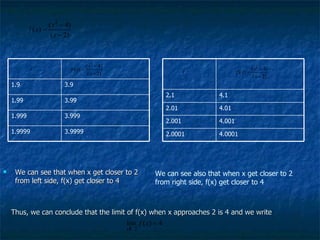
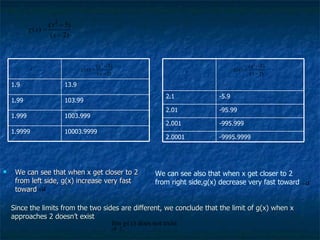
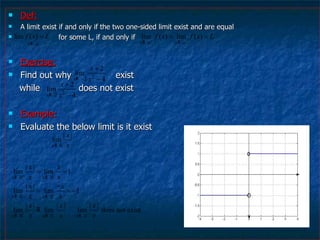
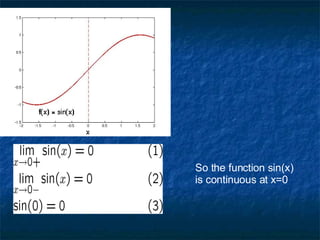
1) The document discusses limits, continuity, and tangent lines. It provides definitions of limits and continuity, and examples of evaluating one-sided limits. 2) Methods for computing limits of polynomials, rational functions, and piecewise functions are presented along with theorems about continuity of functions. 3) The concept of asymptotes is introduced as limits involving infinity. Examples of evaluating various types of limits are worked out.

1. Chapter 2 Limit and continuity Tangent lines and length of the curve The concept of limit Computation of limit Continuity Limit involving infinity (asymptotes

2. 1)Tangent lines and the length of the curve Tangent line

3. Lets zoom the graph Now we can see that the slope get closer To get the correct tangent line of the graph at any point, we need to zoom the graph as can as possible

4. The length of curve

5. 2)The concept of limit Example 1 f is not defined at x=2 Example 2 g is not defined at x=2

6. Thus, we can conclude that the limit of f(x) when x approaches 2 is 4 and we write We can see that when x get closer to 2 from left side, f(x) get closer to 4 We can see also that when x get closer to 2 from right side, f(x) get closer to 4 3.9999 1.9999 3.999 1.999 3.99 1.99 3.9 1.9 4.0001 2.0001 4.001 2.001 4.01 2.01 4.1 2.1

7. Since the limits from the two sides are different, we conclude that the limit of g(x) when x approaches 2 doesn’t exist We can see that when x get closer to 2 from left side, g(x) increase very fast toward We can see also that when x get closer to 2 from right side,g(x) decrease very fast toward 10003.9999 1.9999 1003.999 1.999 103.99 1.99 13.9 1.9 -9995.9999 2.0001 -995.999 2.001 -95.99 2.01 -5.9 2.1

8. Def: A limit exist if and only if the two one-sided limit exist and are equal for some L, if and only if Exercise: Find out why exist while does not exist Example: Evaluate the below limit is it exist

9. 3)Computation of the limit Theorem1: Example evaluate the following limits Theorem2: For any Polynomial p(x) and any real number a, Theorem 3: suppose that , then Example: evaluate

10. Theorem 4: Example: evaluate the following limit Theorem 5 (squeeze theorem) Suppose that for all x in some interval and for some number L, then also Example: evaluate the limit Example : ( a limit of piecewise-defined function)

11. 4)Continuity of Functions Definition A function f is continuous at a point x = a if is defined

12. So the function sin(x) is continuous at x=0

13. So the function f(x) is not continuous at x=3

14. So the function f(x) is not continuous at x=0

15. Example Solution

16. example Solution

17. Problem 14 Answer Removable Removable Not removable

18. Theorem 1 All Polynomial are continuous everywhere, is continuous for all x if n is odd, and continuous for all x 0 if n is even. Also is continuous for all , and for Theorem 3 Suppose that and is continuous at , then Theorem 2 Suppose that f(x) and g(x) are continuous at x=a, then (f+g)(x) is continuous at x=a (f-g)(x) is continuous at x=a (f.g)(x) is continuous at x=a (f/g)(x) is continuous at x=a if g(a) 0 Example Determine where is continuous? Corollary Suppose that is continuous at and is continuous at , then is continuous at

19. Practice on continuity Exercise 11 : explain why each function is discontinuous at the given point by indicating which of the three condition in definition are not met Exercise 23,19 : find all discontinuity of f(x). If the discontinuity is removable, introduce the new function that remove the discontinuity: Exercise 34 : determine the value of a and b that make the given function continuous

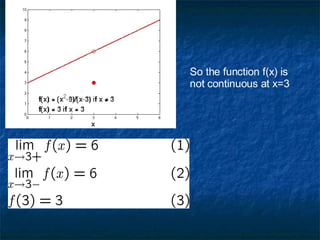
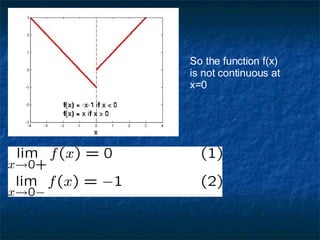
20. Theorem4 : (intermediate value theorem) Suppose that is continuous on closed interval [a, b], and W is any number between f(a) and f(b). Then, there is a number For which corollary2 : Suppose that f(x) is continuous on closed interval (a, b), and f(a) and f(b) have opposite signs (f(a).f(b)<0), so there is at least one number for which f(c)=0

21. Limit involving infinity, Asymptotes Example 1: