The document presents an overview of machine learning approaches in robotics, specifically focusing on direct policy learning and reward learning methods within the framework of reproducing kernel Hilbert spaces (RKHS). It discusses the theoretical foundations of these methods, including regression techniques and kernel-based approaches, and outlines various applications in reinforcement learning and inverse reinforcement learning. The conclusion emphasizes the importance of selecting appropriate algorithms for effective learning from data.

1. DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING
SEOUL NATIONAL UNIVERSITY
Robot, Learning From Data
: Direct Policy Learning in RKHS
& Inverse Reinforcement Learning Methods
Presenter: Sungjoon Choi
Cyber-Physical Systems Laboratory (CPSLAB)
Seoul National University

2. CPSLAB (http://cpslab.snu.ac.kr)
2Learning From Data
https://canvas.northwestern.edu/courses/20122/assignments/syllabus

3. CPSLAB (http://cpslab.snu.ac.kr)
3Learning From Data

4. CPSLAB (http://cpslab.snu.ac.kr)
Contents
4Learning From Data
Learning from Demonstration
Direct Policy Learning Reward Learning
Kernel Methods
Reproducing Kernel Hilbert Space
Learning Theory in RKHS
Inverse Reinforcement Learning Methods

5. CPSLAB (http://cpslab.snu.ac.kr)
Learning From Demonstration
5Learning From Data
Human Expert
http://villains.wikia.com/wiki/Chef_Skinner
http://www.filmspotting.net/forum/index.php?topic=12312.660
Learning from Demonstration
http://blogs.disney.com/oh-my-disney/2014/09/04/learn-to-love-cooking-with-ratatouille/
Execute in Unseen Environments

6. CPSLAB (http://cpslab.snu.ac.kr)
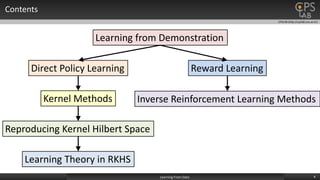
Learning From Demonstration
6Learning From Data
There are two approaches: direct policy learning and reward learning.
Direct policy learning Reward learning
• Try to find a policy function which maps a state
space to an action space.
State
space, 𝑆
Action
space, 𝐴
Policy function
𝜋: 𝑆 → 𝐴
• Cast the learning problem to regression or multi-class
classification problem.
• Standard learning theory or approximation theory are
often used to analyze the performance of learning.
• Try to find a reward function indicating how ‘good’
each state-action pair is.
Joint State-
Action space,
S × 𝐴
Reward
space, 𝑅
• “The reward function, rather than the policy, is the most
succint, robust, and transferable definition of the task.” [1]
[1] Ng, Andrew Y., and Stuart J. Russell. "Algorithms for inverse reinforcement learning." ICML. 2000.
• Often refer to as an Inverse Reinforcement Learning
(IRL) problem.

7. CPSLAB (http://cpslab.snu.ac.kr)
7Learning From Data
Direct Policy Learning

8. CPSLAB (http://cpslab.snu.ac.kr)
Direct Policy Learning in Reproducing Kernel Hilbert Space (RKHS)
8Learning From Data
State
space, 𝑆
Action
space, 𝐴
Policy function
𝜋: 𝑆 → 𝐴
We will see this problem as a nonlinear regression problem.
• In particular, we will use kernel-based regression method.
• RKHS refers to as a reproducing kernel Hilbert space 𝐻 where our policy function
is included, 𝜋 ∈ 𝐻, in other words, the hypothesis space.
We will also focus on how well this function generalizes, that is, how well it
estimates the outputs for previously unseen inputs based in learning theory.

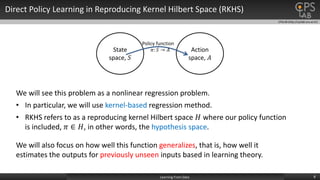
9. CPSLAB (http://cpslab.snu.ac.kr)
Definition and Existence Reproducing Kernel Hilbert Space
9Learning From Data
Existence of the RKHS is shown by Moore-Aronszajn theorem.
Following is the definition of the reproducing kernel Hilbert space. [1]
[1] Rasmussen, Carl Edward. "Gaussian processes for machine learning." (2006).

10. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space
10Learning From Data
Existence of the RKHS is shown by Moore-Aronszajn theorem.
Following is the definition of the reproducing kernel Hilbert space. [1]
[1] Rasmussen, Carl Edward. "Gaussian processes for machine learning." (2006).
What…?

11. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 1
11Learning From Data
The first thing that might come into your mind when you hear about kernel methods
would be transferring input data into the feature space.
What Mercer’s theorem say is that every kernel function can be expressed as an inner-
product of infinite (finite for degenerate kernels) dimensional eigenvectors.

12. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 1
12Learning From Data
Suppose we are given a kernel function 𝑘 𝑥, 𝑥′ = 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖
′
𝑥′ .
From the Mercer’s theorem, we have infinite number of basis (eigen) function 𝜙𝑖 𝑥 :
𝑘 𝑥, 𝑥′ = 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖
′
𝑥′ .
Then, let’s think about a vector space 𝐻 spanned by the eigenfunctions:
𝑓 𝑥 = 𝑖=1
∞
𝑓𝑖 𝜙𝑖 𝑥 and 𝑔 𝑥 = 𝑗=1
∞
𝑔𝑗 𝜙𝑗 𝑥
If we define the inner product of this space 𝐻 as 𝑓, 𝑔 𝐻 = 𝑖=1
∞ 𝑓 𝑖 𝑔 𝑖
𝜆 𝑖
, this space satisfies
the reproducing property! In other words, this space spanned with eigenfunctions
(features) is a RHKS!!
Reproducing property: 𝑓 ⋅ , 𝑘 ⋅, 𝑥 𝐻 = 𝑓 𝑥
Check!
 𝑓 ⋅ , 𝑘 𝑥,⋅ 𝐻 = 𝑖=1
∞
𝑓𝑖 𝜙𝑖 𝑥 , 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖 ⋅ 𝐻 = 𝑖=1
∞ 𝑓 𝑖 𝜆 𝑖 𝜙 𝑖 𝑥
𝜆 𝑖
= 𝑓 𝑥
By definition

13. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 1
13Learning From Data
Suppose we are given a kernel function 𝑘 𝑥, 𝑥′ = 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖
′
𝑥′ .
From the Mercer’s theorem, we have infinite number of basis (eigen) function 𝜙𝑖 𝑥 :
𝑘 𝑥, 𝑥′ = 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖
′
𝑥′ .
Then, let’s think about a vector space 𝐻 spanned by the eigenfunctions:
𝑓 𝑥 = 𝑖=1
∞
𝑓𝑖 𝜙𝑖 𝑥 and 𝑔 𝑥 = 𝑗=1
∞
𝑔𝑗 𝜙𝑗 𝑥
If we define the inner product of this space 𝐻 as 𝑓, 𝑔 𝐻 = 𝑖=1
∞ 𝑓 𝑖 𝑔 𝑖
𝜆 𝑖
, this space satisfies
the reproducing property! In other words, this space spanned with eigenfunctions
(features) is a RHKS!!
Reproducing property: 𝑓 ⋅ , 𝑘 ⋅, 𝑥 𝐻 = 𝑓 𝑥
Check!
 𝑓 ⋅ , 𝑘 𝑥,⋅ 𝐻 = 𝑖=1
∞
𝑓𝑖 𝜙𝑖 𝑥 , 𝑖=1
∞
𝜆𝑖 𝜙𝑖 𝑥 𝜙𝑖 ⋅ 𝐻 = 𝑖=1
∞ 𝑓 𝑖 𝜆 𝑖 𝜙 𝑖 𝑥
𝜆 𝑖
= 𝑓 𝑥
By definition
What…?

14. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 2
14Learning From Data
The RKHS 𝐻 has two properties:
1. For every 𝑥, 𝑘 𝑥, 𝑥′ as a function of 𝑥′ belongs to 𝐻.
2. 𝑘 𝑥, 𝑥′ has a reproducing property.
 𝑓 ⋅ , 𝑘 ⋅, 𝑥 𝐻 = 𝑓 𝑥
Suppose our kernel function is
𝑘 𝑥, 𝑥′ = exp
− 𝑥 − 𝑥′
2
2
𝑙2
Then, from the Moore-Aronszajn theorem, there exists a RKHS 𝐻.
But, what does this mean?
We want to define a space of functions 𝐻 whose element 𝑓 ∈ 𝐻 has following form:
𝑓 𝑥 = 𝑖=1
𝑛
𝛼𝑖 𝑘 𝑧𝑖, 𝑥
for some 𝑛 ∈ 𝑁.

15. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 2
15Learning From Data
We want to define a space of functions 𝐻 whose element 𝑓 ∈ 𝐻 has following form:
𝑓 𝑥 = 𝑖=1
𝑛
𝛼𝑖 𝑘 𝑧𝑖, 𝑥
for some 𝑛 ∈ 𝑁.
The RKHS 𝐻 has two properties:
1. For every 𝑥, 𝑘 𝑥, 𝑥′ as a function of 𝑥′ belongs to 𝐻.
2. 𝑘 𝑥, 𝑥′ has a reproducing property.
 𝑓 ⋅ , 𝑘 ⋅, 𝑥 𝐻 = 𝑓 𝑥
Then, this space satisfies the reproducing property:
 𝑘 ⋅, 𝑥 , 𝑘 ⋅, 𝑥′ 𝐻 = 𝑘 𝑥, 𝑥′
 𝑓 ⋅ , 𝑘 ⋅, 𝑥 = 𝑖 𝛼𝑖 𝑘 𝑧𝑖,⋅ , 𝑘 ⋅, 𝑥 𝐻 = 𝑖 𝛼𝑖 𝑘 𝑧𝑖,⋅ , 𝑘 ⋅, 𝑥 = 𝑖 𝛼𝑖 𝑘 𝑧𝑖, 𝑥 = 𝑓 𝑥
If we define the inner-product of the Hilbert space as
𝑖 𝛼𝑖 𝑘 ⋅, 𝑥𝑖 , 𝑗 𝛽𝑗 𝑘 ⋅, 𝑥𝑗′ 𝐻 = 𝑖 𝑗 𝛼𝑖 𝛽𝑗 𝑘 𝑥𝑖, 𝑥𝑗′

16. CPSLAB (http://cpslab.snu.ac.kr)
Reproducing Kernel Hilbert Space – Approach 2
16Learning From Data
We want to define a space of functions 𝐻 whose element 𝑓 ∈ 𝐻 has following form:
𝑓 𝑥 = 𝑖=1
𝑛
𝛼𝑖 𝑘 𝑧𝑖, 𝑥
for some 𝑛 ∈ 𝑁.
If we define the inner-product of the Hilbert space as
𝑖 𝛼𝑖 𝑘 ⋅, 𝑥𝑖 , 𝑗 𝛽𝑗 𝑘 ⋅, 𝑥𝑗′ 𝐻 = 𝑖 𝑗 𝛼𝑖 𝛽𝑗 𝑘 𝑥𝑖, 𝑥𝑗′
The space defined with as above is a reproducing kernel Hilbert space.
 As 𝑓 𝐻 must be greater equal to zero, kernel function 𝑘 𝑥, 𝑥′ should be positive
semi-definite!
 A norm 𝑓 𝐻 is defined as follows:
𝑓 𝐻
2
= 𝑓, 𝑓 𝐻 = 𝑖 𝑗 𝛼𝑖 𝛼𝑗 𝑘 𝑥𝑖, 𝑥𝑗
′
= 𝛼 𝑇 𝐾 𝑋, 𝑋 𝛼.

17. CPSLAB (http://cpslab.snu.ac.kr)
Practical Usage
17Learning From Data
Empirical risk minimization with Hilbert norm regularization
min
𝑓∈𝐻 𝑖=1
𝑁
𝑓 𝑥𝑖 − 𝑦𝑖
2 + 𝛾 𝑓 𝐻
2
If we set our hypothesis space 𝐻 as radial basis function networks,
𝑓 𝑥 = 𝑗=1
𝑛
𝛼𝑗 𝑘 𝑥, 𝑧𝑗 ,
then the optimization becomes
min
𝛼∈𝑅 𝑛 𝑖=1
𝑁
𝑗
𝑛
𝛼𝑗 𝑘 𝑥𝑖, 𝑧𝑗 − 𝑦𝑖
2
+ 𝛾𝛼 𝑇 𝐾 𝑍, 𝑍 𝛼
If we rewrite in a matrix form,
min
𝛼∈𝑅 𝑛
𝐾 𝑋𝑍 𝛼 − 𝑌 2
2
+ 𝛾𝛼 𝑇 𝐾𝑍𝑍 𝛼
which is a quadratic programming with respect to 𝑛 dimensional vector 𝛼.

18. CPSLAB (http://cpslab.snu.ac.kr)
Practical Usage
18Learning From Data
min
𝛼∈𝑅 𝑛
𝐾 𝑋𝑍 𝛼 − 𝑌 2
2
+ 𝛾𝛼 𝑇 𝐾𝑍𝑍 𝛼
𝐾 𝑋𝑍
𝛼
𝑌
𝛼 𝑇
𝐾𝑍𝑍 𝛼
If Z is identical to 𝑋, then the above equation is identical to Gaussian process regression
or kernel ridge regression.
In practice, we can add additional constraints such as 𝛽𝛼 𝑇 𝛼 or 𝛼 ∞ ≤ 𝑀 which greatly
increases the stability issue!
Often referred to as a sparse Gaussian process regression with inducing points.

19. CPSLAB (http://cpslab.snu.ac.kr)
Learning Theory
19Learning From Data
Suppose our training data 𝑧 𝑚 = 𝑥𝑖, 𝑦𝑖 𝑖=1
𝑚
be sampled from 𝑃 𝑥, 𝑦 .
The expected risk of a function 𝑓 ⋅ is defined as:
𝐼 𝑓 = 𝑋×𝑌
𝑦 − 𝑓 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦.
Then, the expected risk can be decomposed into
𝐼 𝑓 =
𝑋×𝑌
𝑦 − 𝑓𝜌 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦 +
𝑋×𝑌
𝑓 𝑥 − 𝑓𝜌 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦
where 𝑓𝜌 𝑥 = 𝑦 ⋅ 𝑃 𝑦|𝑥 𝑑𝑦 is the regression function.

20. CPSLAB (http://cpslab.snu.ac.kr)
Learning Theory
20Learning From Data
𝐼 𝑓 =
𝑋×𝑌
𝑦 − 𝑓𝜌 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦 +
𝑋×𝑌
𝑓 𝑥 − 𝑓𝜌 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦
𝑋×𝑌
𝑦 − 𝑓𝜌 𝑥
2
𝑃 𝑥, 𝑦 𝑑𝑥𝑑𝑦
𝑋
𝑓 𝑥 − 𝑓𝜌 𝑥
2
𝑃 𝑥 𝑑𝑥
Expected Risk = Intrinsic Error + Estimation Error
Intrinsic Error (approximation error)
Estimation Error
We cannot handle this.
We can handle only part of this.

21. CPSLAB (http://cpslab.snu.ac.kr)
Learning Theory
21Learning From Data
The goal of the learning theory is to minimize following functional:
𝐿 𝑓 = 𝑥∈𝑋
𝑓 𝑥 − 𝑓𝜌 𝑥
2
𝑃 𝑥 𝑑𝑥.
𝐿 𝑓 = 𝑓𝜌 − 𝑓
𝐿2 𝑃
2
is often called generalization error.
[1] Niyogi, Partha, and Federico Girosi. "On the relationship between generalization error, hypothesis
complexity, and sample complexity for radial basis functions." Neural Computation 8.4 (1996): 819-842.
If we use a radial basis function network, 𝑓 𝑥 = 𝑖=1
𝑛
𝑔𝑖 exp
𝑥−𝑧 𝑖
2
𝑙 𝑖
2 , we can
achieve following bound on the generalization error [1].
with probability at least 1 − 𝛿.

22. CPSLAB (http://cpslab.snu.ac.kr)
Learning Theory
22Learning From Data
[1] Niyogi, Partha, and Federico Girosi. "On the relationship between generalization error, hypothesis
complexity, and sample complexity for radial basis functions." Neural Computation 8.4 (1996): 819-842.
There are two sources of errors:
1. We are trying to approximate an infinite dimensional object, the regression
function 𝑓0 with a finite number of parameters (approximation error).
Approximation error: 𝑂
1
𝑛
2. We minimize the empirical risk and obtain 𝑓𝑛,𝑙, rather than minimizing the
expected risk (estimation error).
Estimation error: 𝑂
𝑛𝑘 ln 𝑛𝑙 −ln 𝛿
𝑙
0.5

23. CPSLAB (http://cpslab.snu.ac.kr)
23Learning From Data
Reward Learning

24. CPSLAB (http://cpslab.snu.ac.kr)
Reward Learning
24Learning From Data
Understanding basic concept of solving Markov decision process (MDP) or
reinforcement learning (RL) is crucial in a reward learning problem.
Goal of RL is to find a policy function which maximizes an expected sum of rewards:
If we define 𝜇 𝑠, 𝑎 = 𝜇 𝜋 𝑠 𝜋 𝑠, 𝑎 , then the optimization becomes,
max
𝜇 𝑠,𝑎
〈𝜇, 𝑅〉
𝑠. 𝑡. 𝜇 ∈ 𝐺 𝜇
Where 𝐺 𝜇 is often called Bellman flow constraint.

25. CPSLAB (http://cpslab.snu.ac.kr)
Inverse Reinforcement Learning
25Learning From Data
max
𝜇 𝑠,𝑎
〈𝜇, 𝑅〉
𝑠. 𝑡. 𝜇 ∈ 𝐺 𝜇
True reward 𝑅 True density 𝜇 State-action traj.
Solving MDP
State-action traj. max
𝑅∈𝐻 𝑅
〈𝜇, 𝑅〉
Solving IRL
Estimated reward 𝑅
http://users.eecs.northwestern.edu/~argall/learning.html

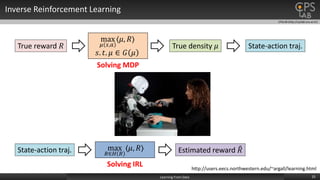
26. CPSLAB (http://cpslab.snu.ac.kr)
Inverse Reinforcement Learning Methods
26Learning From Data
NR [1]
MMP [2]
AN [3]
MaxEnt [4]BIRL [6] RelEnt [7]
StructIRL [8] GPIRL [5]
DeepIRL [9]
[1] Ng, Andrew Y., and Stuart J. Russell. "Algorithms for inverse reinforcement learning." ICML, 2000.
[2] Ratliff, Nathan D., J. Andrew Bagnell, and Martin A. Zinkevich. "Maximum margin planning." ICML, 2006.
[3] Abbeel, Pieter, and Andrew Y. Ng. "Apprenticeship learning via inverse reinforcement learning." ICML, 2004.
[4] Ziebart, Brian D., Andrew Maas, J.Andrew Bagnell, and Anind K. Dey, "Maximum Entropy Inverse Reinforcement Learning."AAAI. 2008.
[5] Levine, Sergey, Zoran Popovic, and Vladlen Koltun. "Nonlinear inverse reinforcement learning with Gaussian processes." NIPS 2011.
[6] Ramachandran, Deepak, and Eyal Amir. "Bayesian inverse reinforcement learning.“, AAAI, 2007
[7] Boularias, Abdeslam, Jens Kober, and Jan R. Peters. "Relative entropy inverse reinforcement learning." AISTATS. 2011.
[8] Klein, Edouard, Matthieu Geis, Bilal Piot, and Olivier Pietquin, "Inverse reinforcement learning through structured classification." NIPS. 2012.
[9] Wulfmeier, Markus, Peter Ondruska, and Ingmar Posner. "Deep Inverse Reinforcement Learning." arXiv. 2015.

27. CPSLAB (http://cpslab.snu.ac.kr)
Inverse Reinforcement Learning Methods
27Learning From Data
NR [1]
MMP [2]
AN [3]
Maximize discrepancy between expert’s and sampled value.
Objective
Maximize margin between expert’s demonstration and every state-actions.
Minimize value between expert’s and sampled ones.
StructIRL [8] Cast IRL to multi-class classification problem.
NR [1]
MMP [2]
AN [3]
StructIRL [8]

28. CPSLAB (http://cpslab.snu.ac.kr)
Inverse Reinforcement Learning Methods
28Learning From Data
MaxEnt [4]
BIRL [6]
RelEnt [7]
GPIRL [5]
DeepIRL [9]
Objective
Define likelihood of state-action trajectories and use MLE.
MaxEnt [4]
BIRL [6]
Define posterior of state-action trajectories and use MH sampling.
Define likelihood using SGP and use gradient ascent method.
Minimize relative entropy between expert’s and learner’s distribution.
GPIRL [5]
RelEnt [7]
DeepIRL [9]
Model likelihood with neural networks.

29. CPSLAB (http://cpslab.snu.ac.kr)
Conclusion
29Learning From Data
 I believe selecting a proper machine learning algorithm is more than selecting a chocolate
from a chocolate box.
 "Deep Learning is brute force learning. It is not intelligent learning."
 "Machine learning is not only about machines, but also about humans."
- Vladimir Vapnik @ NIPS15
http://www.forbes.com/forbes/welcome/http://aboutintelligence.blogspot.kr/2009/01/vapniks-picture-explained.html
 Robotics deals with humans!

30. CPSLAB (http://cpslab.snu.ac.kr)
30Learning From Data
Thank you for your attention!!
Any Questions?
sungjoon.s.choi@cpslab.snu.ac.kr