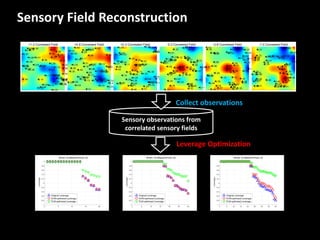
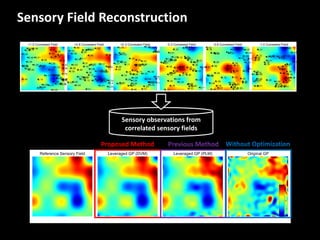
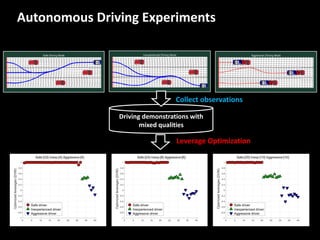
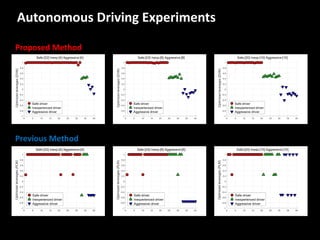
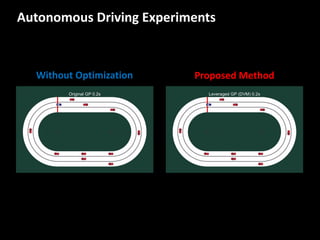
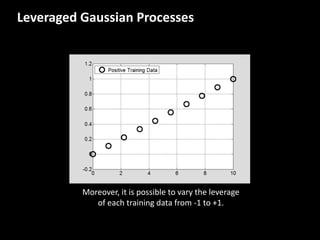
The document discusses leveraged Gaussian process regression, emphasizing its ability to anchor positive training data while avoiding negative data. It introduces a sparse constrained leverage optimization approach to handle the challenges associated with the number of leverage parameters, proposing new methods for more accurate optimization. Additionally, it outlines applications in sensory field reconstruction and autonomous driving experiments, highlighting the advantages of these techniques.






























![Leverage
Optimization
(v1)
Using
proximal
linearized
minimization
[1],
the
update
rule
for
solving
above
optimization
is
[1] J. Bolte, S. Sabach, and M. Teboulle, “Proximal alternating linearized minimization for nonconvex and nonsmooth problems,”
Mathematical Programming, vol. 146, no. 1-2, pp. 459–494, 2014.
where
the
proximal
mapping
becomes
soft-‐thresholding:
where
𝛾̅ = 𝛾 − 1.](https://image.slidesharecdn.com/kernelrkhsandgp-170328222447/85/Kernel-RKHS-and-Gaussian-Processes-39-320.jpg)