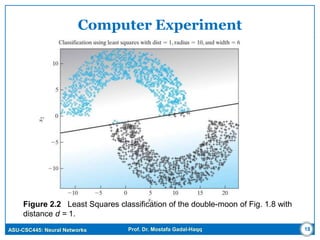
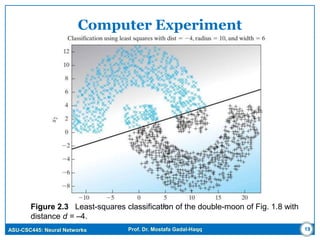
The document discusses regression models for modeling relationships between input and output variables. It covers linear regression, using linear functions to model the relationship, and nonlinear regression, using nonlinear functions. Maximum a posteriori (MAP) estimation and least squares estimation are described as approaches for estimating the parameters of regression models from data. MAP estimation maximizes the posterior probability of the parameters given the data and assumes prior probabilities on the parameters, while least squares minimizes error. Regularized least squares is also covered, which adds a regularization term to improve stability. Computer experiments are demonstrated applying linear regression to classification problems.

1. CHAPTER 02
MODEL BUILDING THROUGH
REGRESSION
CSC445: Neural Networks
Prof. Dr. Mostafa Gadal-Haqq M. Mostafa
Computer Science Department
Faculty of Computer & Information Sciences
AIN SHAMS UNIVERSITY
(most of the figures in this presentation are copyrighted to Pearson Education, Inc.)

2. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
 Introduction
 Supervised Learning vs. Regression
 Linear Regression Model
 Maximum a Posteriori Estimation (MAP)
 Computer Experiment
 The Minimum-Description-Length Principle
 Finite Sample Size Consideration
2
Model Building Through Regression

3. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Introduction
 Regression is a special type of function approximation
 There are two types of regression models:
 Linear regression: the dependence of the output on the
input is defined by a linear function
 Nonlinear regression : the dependence of the output on
the input is defined by a nonlinear function
3
y
x
y
x
Linear regression Nonlinear regression

4. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 4
Supervised Learning vs. Regression
 Supervised Learning (Classification):
 Learn the “right answer” for each data sample.
 Regression Problem:
 Predict the real-valued output using the data samples.

5. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Introduction
 In regression we do the following:
 One of the random variables is considered to be of
particular interest and is referred to as a dependant
variable, or response (The output).
 The remaining random variables are called
independent variables, or regressor (The input).
 The dependence of the response on the regressors
includes an additive error term.
5

6. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Linear Regression Model
 Linear Regression (One variable)
 The parameter vector w = [ w0 w1 ] is fixed but unknown;
stationary environment.
bay  x
6
y
x
Linear regression
01 x wwy 
a = slope
b = intercept

7. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Linear Regression Model
 Linear Regression (Multiple variables)
 The parameter vector w is
fixed but unknown;
stationary environment.
Figure 2.1(a) Unknown stationary stochastic environment.
(b) Linear regression model of the environment.



M
j
jjxwd
1

 xwT
d
7
T
Mxxx ],...,,[ 21x

8. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 8
Linear Regression Model
 Preliminary Considerations:
 With the environment being stochastic, it follows that: the
regressor x, the response d, and the expectational error 
are sample values of the random variables X, D, and E.
 Then, we can state the problem as follows:
 Given the joint statistics of the regressor X and the
corresponding response D, estimate the unknown
parameter vector w.
 By joint statistics we mean that we have:
 The correlation matrix of the regressor X;
 The variance of the desired response D;
 The cross-correlation vector of X and D.
 It is assumed that the means of both X and D are zero.

9. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 9
Linear Regression Model
How to estimate the parameter vector W?
 Maximum A Posteriori (MAP)
 Least Squares Estimation (LS)
 Regularized Least Squares Estimation (RLS)

10. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 10
Maximum A Posteriori (MAP) Estimation
 Estimation of the parameter vector w:
 The regressor X bears no relation to the parameter vector w.
 Information about w is contained in the desired response D.
 Then we focus on the joint probability density of w
and D conditional on X:
 Which gives a special form of Bayes theorem:
)(),|()(),|()|,( wxwxwxw pdpdpdpdp 
)(
)(),|(
),|(
dp
pdp
dp
wxw
xw 

11. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 11
Maximum A Posteriori (MAP) Estimation
 Observation density: p(d|w,x), referring to the observation of
the environmental response d due to the regressor x, given w.
Also, it is called the likelihood l(d|w,x).
 Prior: p(w), referring to information about the parameter vector
w, prior to any observations.
 Posterior density: p(w|d,x), referring to the parameter vector w
after observations have been completed.
 Evidence: p(d), referring to the information contained in the
environmental response.
)(
)(),|(
),|(
dp
pdp
dp
wxw
xw 

12. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 12
Maximum A Posteriori (MAP) Estimation
 Since p(d) is a normalization constant, we can write:
 The Maximum-Likelihood (ML) estimate of the vector w is:
 The Maximum a Posteriori (MAP) estimate of the vector w is:
 The MAP is more profound than the ML because the ML
estimator relies solely on the observation model (d, x), which
may lead to non-unique solution. The MAP estimator enforce
uniqueness and stability to the solution by including p(w).
)(),|(),|( wxwxw pdldp 
),|(maxarg xww
w
dlML 
),|(maxarg xww
w
dpMAP 

13. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 13
Maximum A Posteriori (MAP) Estimation
 Parameter Estimation in Gaussian Environment:
 Let we have a total of N samples of the training data pairs (x, d).
We have to make the following three assumptions:
1. IID: The N samples are statistically independent and identically
distributed (iid)
2. Gaussianity: The environment, generating the training samples,
is Gaussian distributed.
))(
2
1
exp(
2
1
),|(
)
2
exp(
2
1
)(
2
2
2
2
xwT
iii
i
i
dxwdp
p








14. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 14
Maximum A Posteriori (MAP) Estimation
 Parameter Estimation in Gaussian Environment:
3. Stationarity: The environment is stationary, which mean that
the parameter vector w is fixed but unknown.
 Substitution in Bayes rule leads to the MAP estimation of the
parameter vector as:
 Where  = 2/2
w






 

N
i
i
T
idMAP
1
22
||||
2
)(
2
1
maxˆ wxww
w

)
2
exp(
2
1
)( 2
2
w
i
w
i
w
wp



15. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 15
Maximum A Posteriori (MAP) Estimation
 Parameter Estimation in Gaussian Environment:
 Maximizing the bracket in the previous equation is equivalent to
minimizing the quadratic function:
 By differentiating w.r.t. w and equating to zero, we get the MAP
estimate of w:
 Where the M-by-M correlation matrix, Rxx , and the M-by-1
cross-correlation vector , rdx , are given by:



N
i
i
T
id
1
22
||||
2
)(
2
1
)( wxww

  )()()(ˆ 1
NNN dxxxMAP rIRw 
 
 
 

N
i
iidx
N
i
N
j
T
jixx dNN
11 1
)(and,)( xrxxR

16. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 16
Least-Square (LS)
 The estimator is obtained by minimizing the least square error
in the parameter vector:
 This is identical to the Maximum-likelihood (ML) estimator
 But this solution lacks uniqueness and stability.


N
i
i
T
id
1
2
)(
2
1
)( xww
)()()(ˆ 1
NNN dxxx rRw 


17. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 17
Regularized Least-Square (RLS)
 To overcome this, we add a structural regularization
term, ||w||2, to obtain the regularized least-square
estimator:
 structural regularization term, ||w||2, to obtain the
regularized least-square estimator:
 Which is identical to the MAP estimator.  is called a
regularization parameter. If ~0, it means that we have
complete confidence in the data; if ~ then we have no
confidence in the data.
  )()()(ˆ 1
NNN dxxx rIRw 
 
,w
2
)(
2
1
)(
2
1
2
 



N
i
i
T
id xww

18. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Computer Experiment
18
Figure 2.2 Least Squares classification of the double-moon of Fig. 1.8 with
distance d = 1.

19. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Computer Experiment
19
Figure 2.3 Least-squares classification of the double-moon of Fig. 1.8 with
distance d = –4.

20. •Problems:
•2.1, 2.2
•Computer Experiment
•2.8, 2.10
Homework 2
20

21. The Least Mean Square
Algorithm
Next Time
21