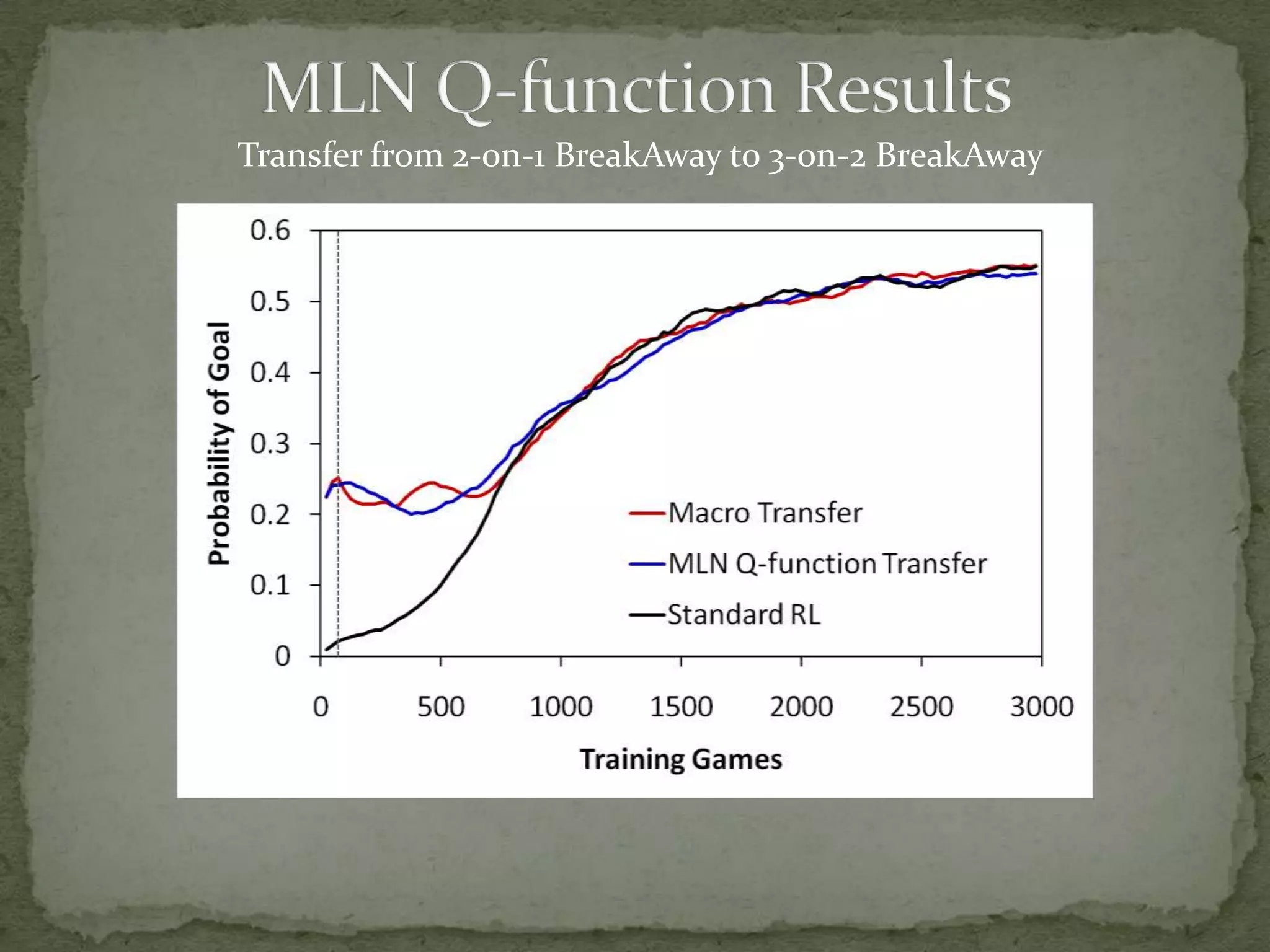
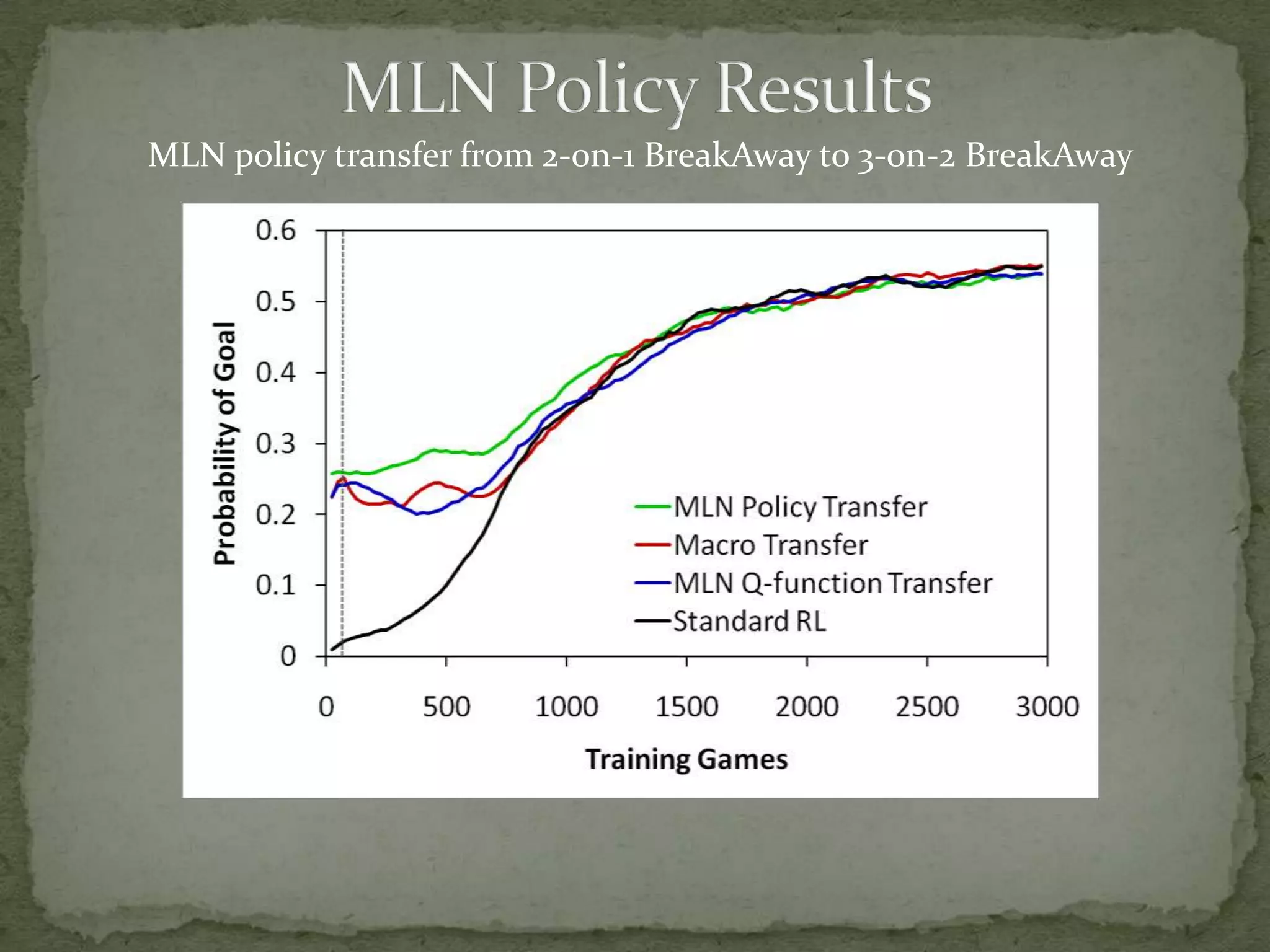
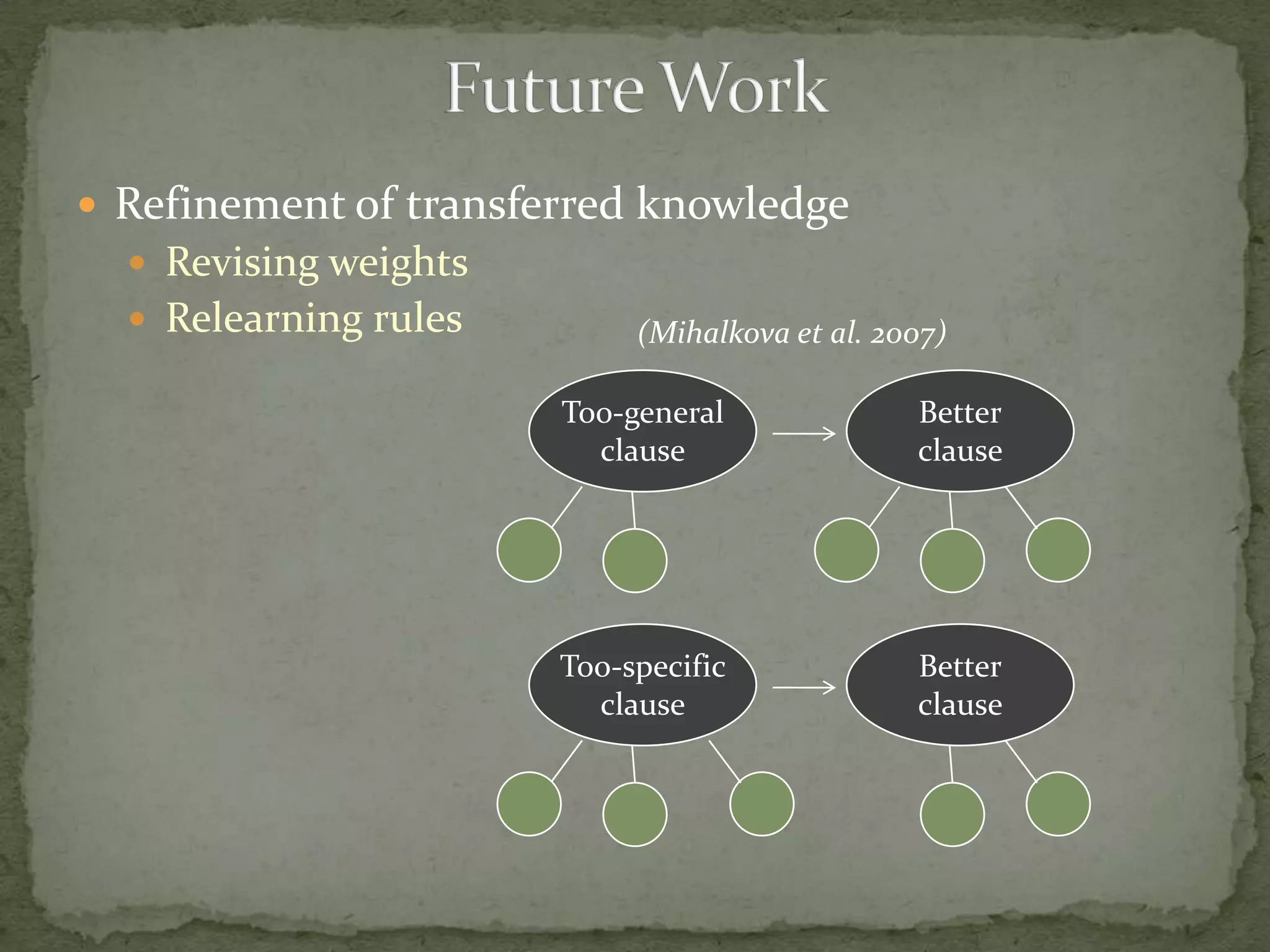
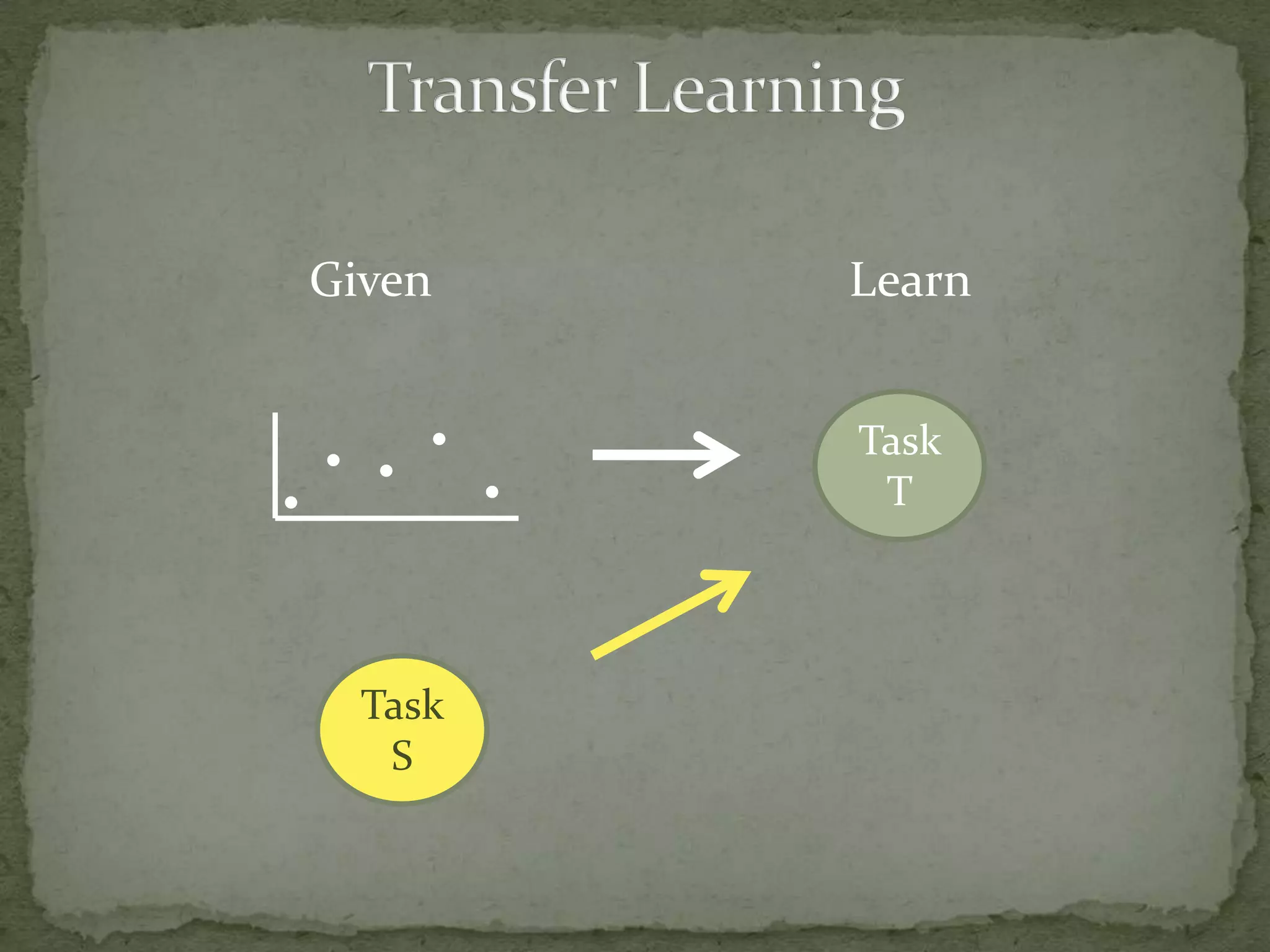
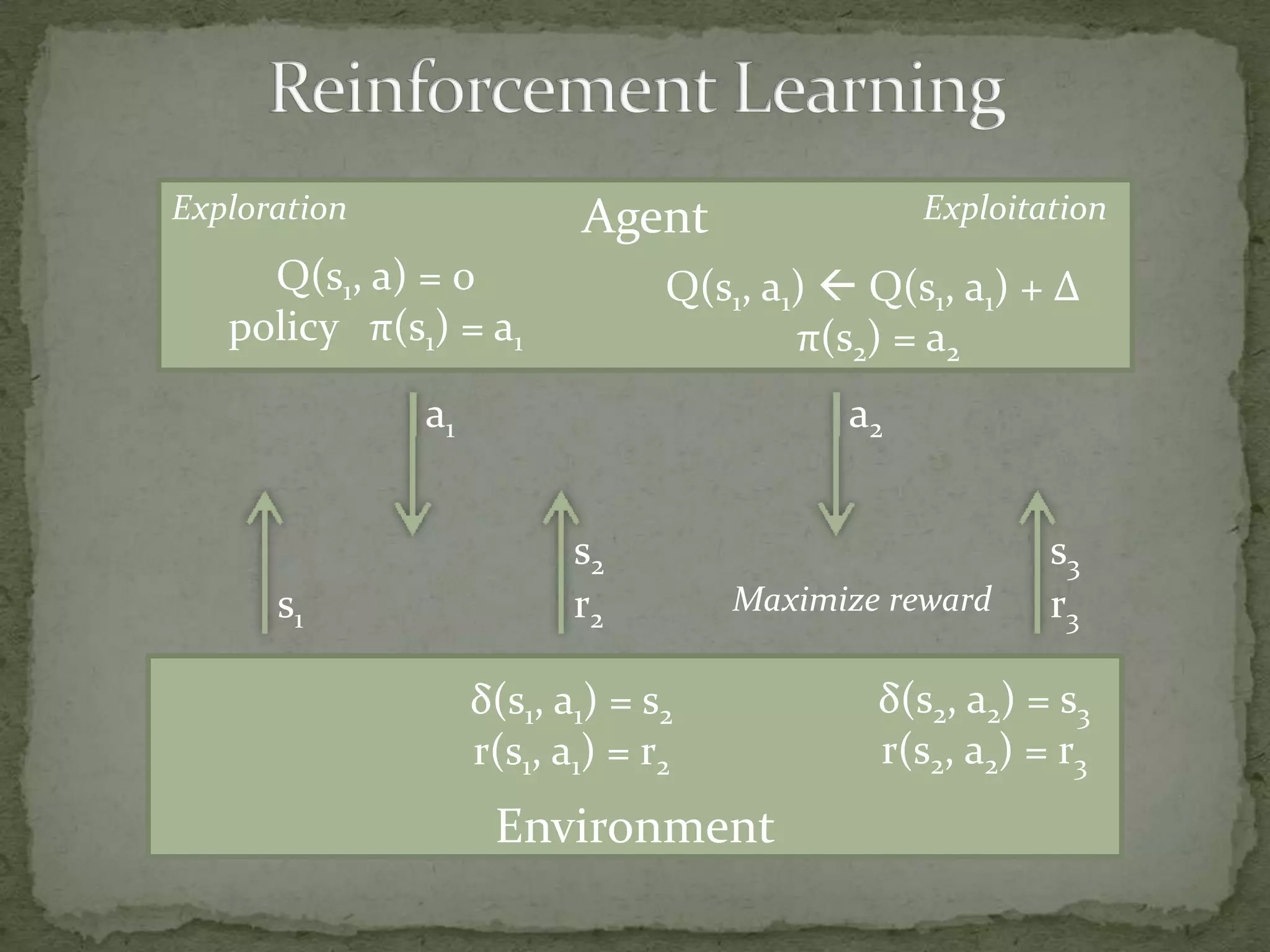
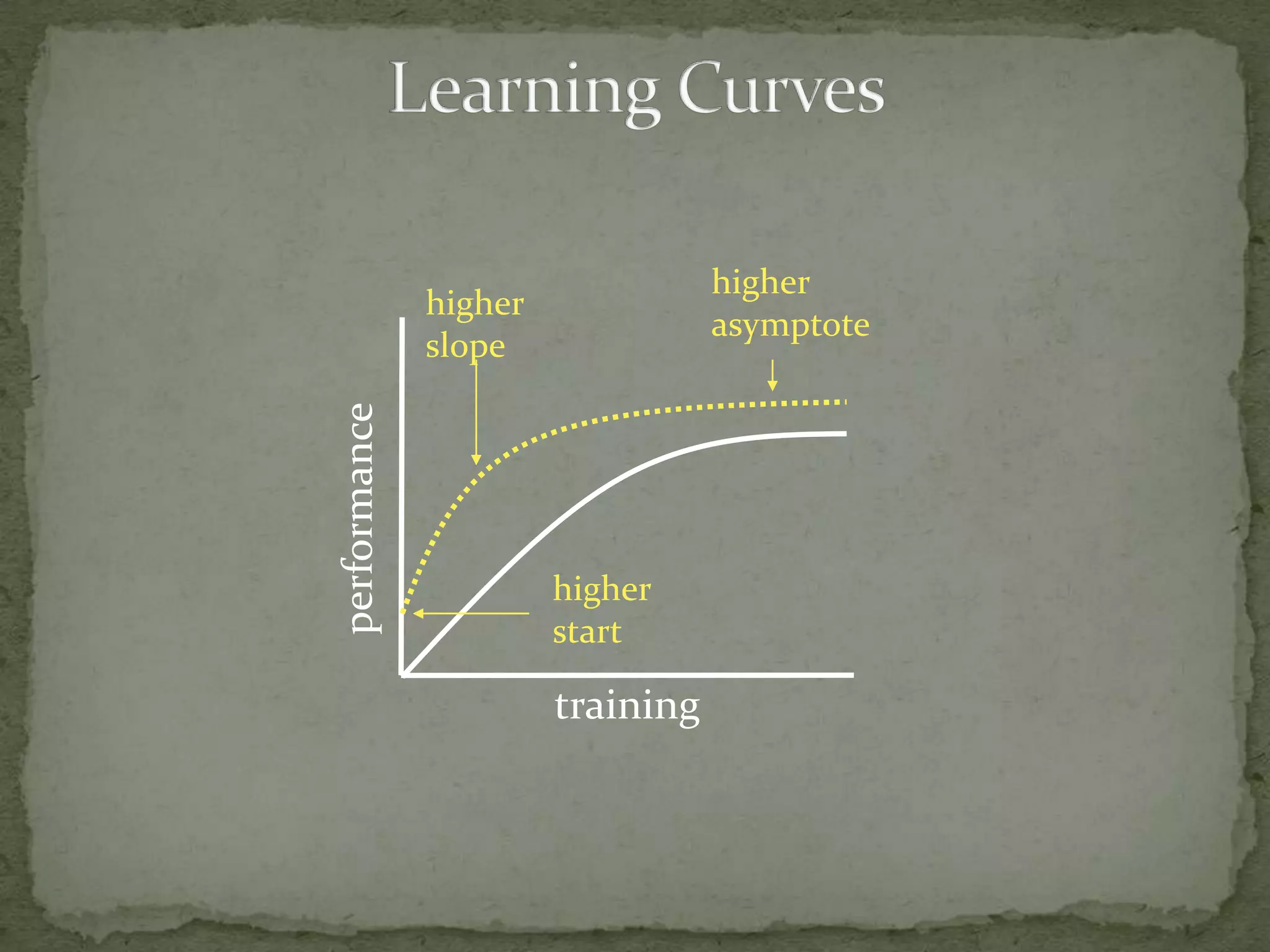
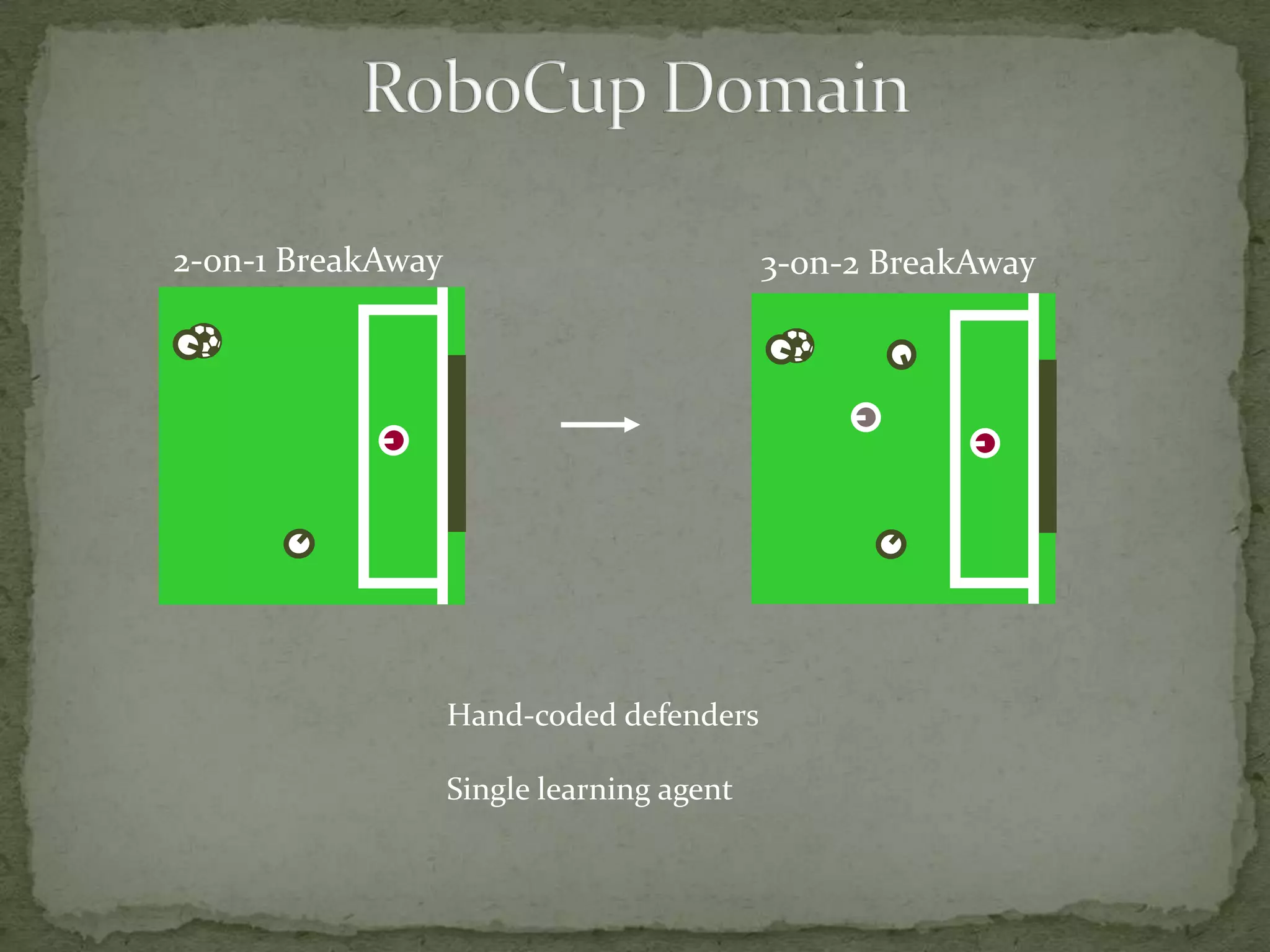
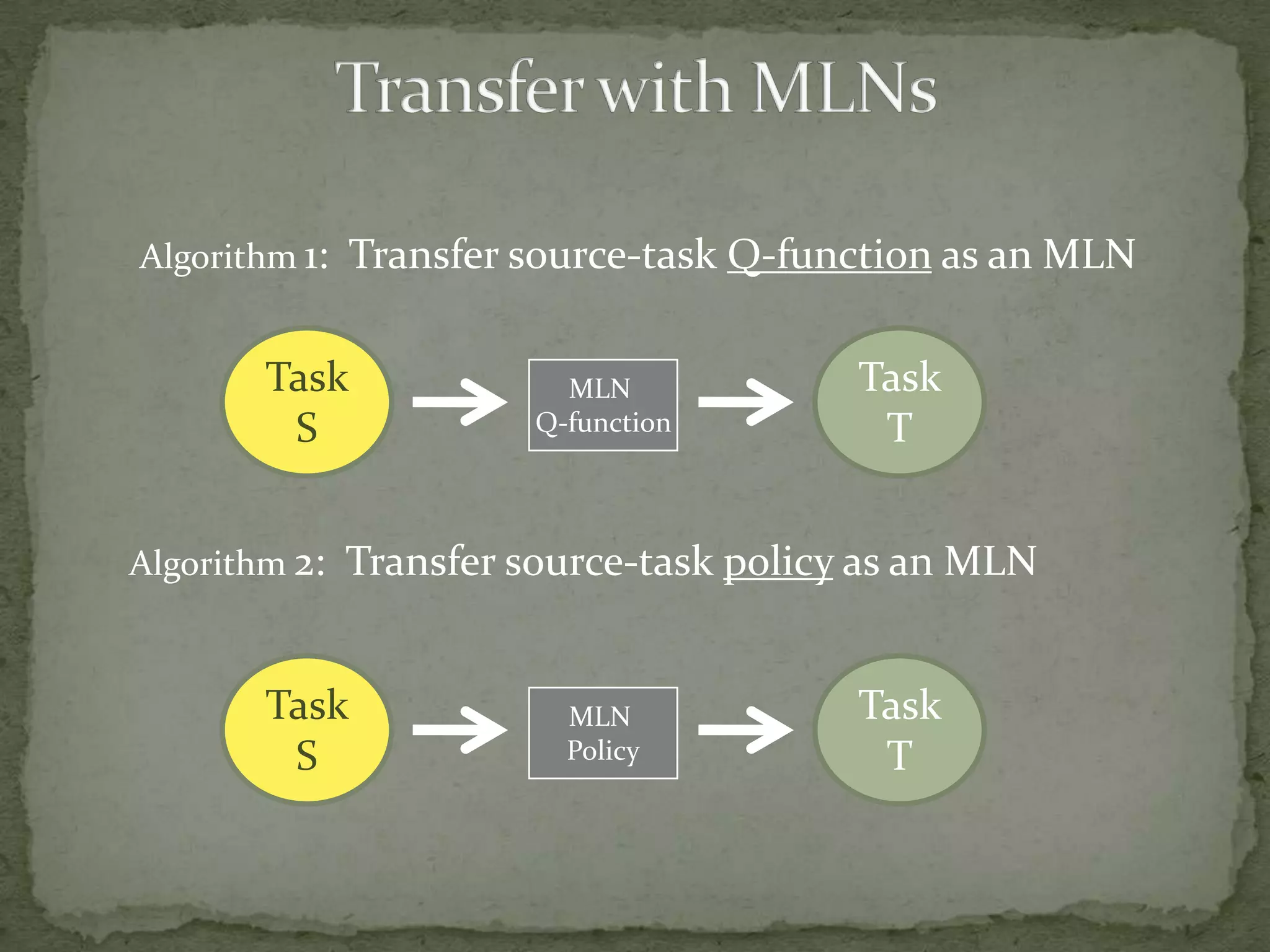
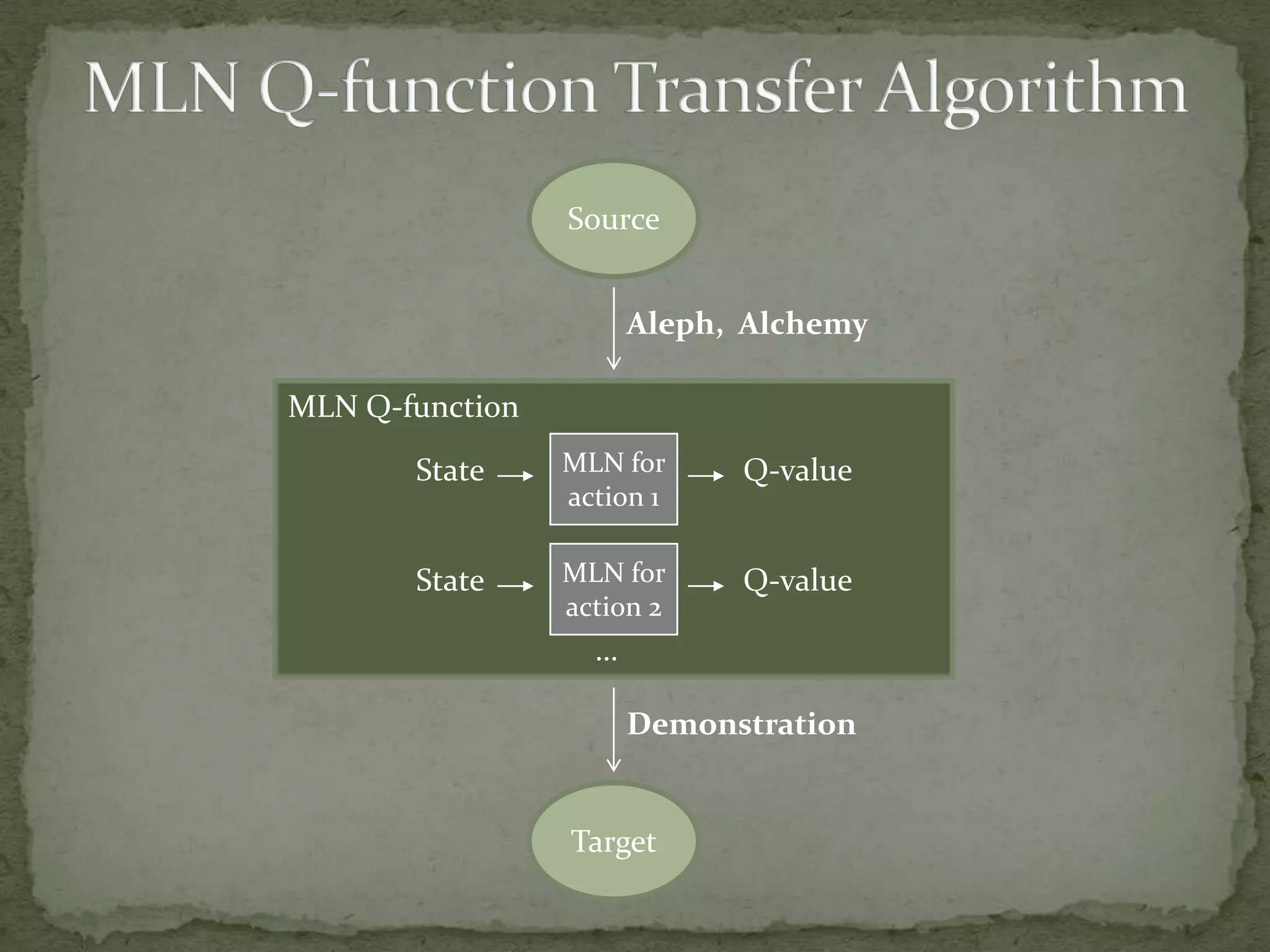
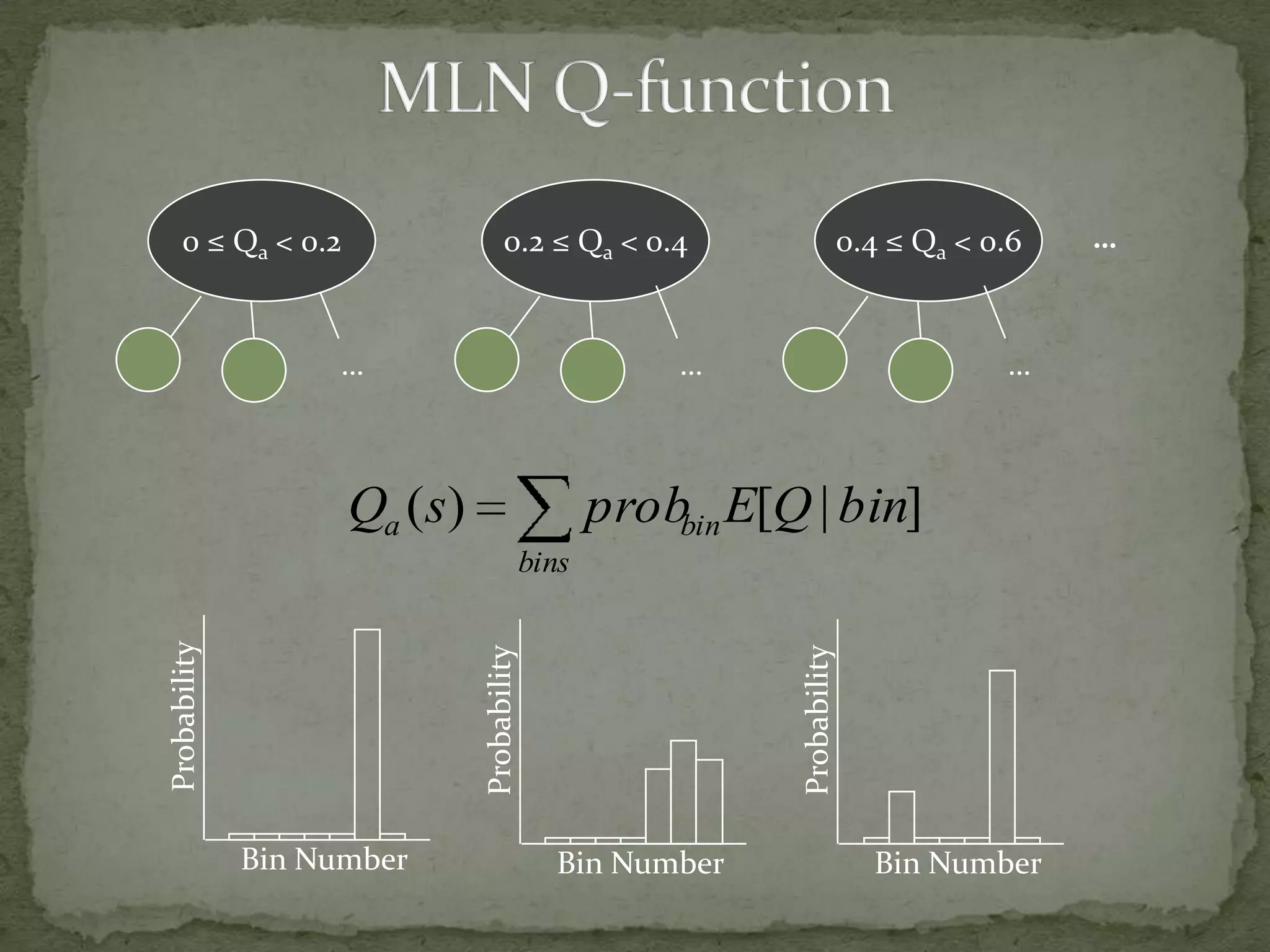
This document summarizes research on using Markov logic networks (MLNs) for transfer learning in reinforcement learning domains. It presents two new algorithms for transferring either a Q-function or policy from a source task to a target task via an MLN. Experimental results show that MLN transfer can improve learning performance in the target task compared to learning from scratch, and that policy transfer often works better than Q-function transfer. However, additional relational knowledge in MLN policies does not always further improve transfer. Future work areas include refining transferred knowledge and exploring relational reinforcement learning using MLNs.

1. Lisa Torrey and Jude ShavlikUniversity of WisconsinMadison WI, USAPolicy Transfer viaMarkov Logic Networks

2. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

3. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

4. Transfer LearningGivenLearnTask TTask S

5. Reinforcement LearningAgentExplorationExploitationQ(s1, a) = 0policy π(s1) = a1Q(s1, a1)  Q(s1, a1) + Δπ(s2) = a2s2s3a1a2r2r3Maximize rewards1Environmentδ(s2, a2) = s3r(s2, a2) = r3δ(s1, a1) = s2r(s1, a1) = r2

6. Learning Curveshigher asymptotehigher slopeperformancehigher starttraining

7. RoboCup Domain2-on-1 BreakAway3-on-2 BreakAwayHand-coded defendersSingle learning agent

8. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

9. Madden & Howley 2004Learn a set of rulesUse during exploration stepsCroonenborghs et al. 2007Learn a relational decision treeUse as an additional actionOur prior work, 2007Learn a relational macroUse as a demonstrationRelated Work

10. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

11. pass(t1)goalLeftpass(t2)goalRightIF distance(GoalPart) > 10AND angle(ball, Teammate, Opponent) > 30THENRelational Transferpass(Teammate)

12. Markov Logic NetworksRichardson and Domingos, Machine Learning 2006Formulas (F)evidence1(X) AND query(X)evidence2(X) AND query(X)Weights (W)w0 = 1.1w1 = 0.9query(x1)query(x2)e1e1……e2e2ni(world) = # true groundings of ith formula in world

13. Transfer with MLNsAlgorithm 1: Transfer source-task Q-function as an MLNTask TTask SMLN Q-functionAlgorithm 2: Transfer source-task policy as an MLNTask TTask SMLN Policy

14. Demonstration MethodUse MLNUse regular target-task training

15. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

16. MLN Q-function Transfer AlgorithmSourceAleph, AlchemyMLN Q-functionMLN foraction 1StateQ-valueMLN foraction 2StateQ-value…DemonstrationTarget

17. MLN Q-functionProbabilityProbabilityProbabilityBin NumberBin NumberBin Number0 ≤ Qa < 0.20.2 ≤ Qa < 0.40.4 ≤ Qa < 0.6…………

18. Learning an MLN Q-functionBins: Hierarchical clusteringIF … THEN 0 < Q < 0.2IF … THEN 0 < Q < 0.2IF … THEN 0 < Q < 0.2Formulas for each bin: Aleph (Srinivasan)w0= 1.1w1 = 0.9…Weights: Alchemy (U. Washington)

19. Selecting Rules to be MLN FormulasAdd torulesetAleph rulesDoes rule increase F-score of ruleset?yesRule 1 Precision=1.0Rule 2 Precision=0.99Rule3 Precision=0.96… …F = 2 x Precision x Recall Precision + Recall

20. MLN Q-function RulesExamples for transfer from 2-on-1 BreakAway to 3-on-2 BreakAwayIF distance(me, GoalPart) ≥ 42 distance(me, Teammate) ≥ 39 THEN pass(Teammate) falls into [0, 0.11]IF angle(topRight, goalCenter, me) ≤ 42 angle(topRight, goalCenter, me) ≥ 55 angle(goalLeft, me, goalie) ≥ 20 angle(goalCenter, me, goalie) ≤ 30THEN pass(Teammate) falls into [0.11, 0.27]IF distance(Teammate, goalCenter) ≤ 9 angle(topRight, goalCenter, me) ≤ 85THEN pass(Teammate) falls into [0.27, 0.43]

21. MLN Q-function ResultsTransfer from 2-on-1 BreakAway to 3-on-2 BreakAway

22. BackgroundApproaches for transfer in reinforcement learningRelational transfer with Markov Logic NetworksTwo new algorithms for MLN transferOutline

23. MLN Policy-Transfer AlgorithmSourceAleph, AlchemyMLN PolicyStateActionMLN(F,W)ProbabilityDemonstrationTarget

24. MLN Policymove(ahead)pass(Teammate)shoot(goalLeft)…………Policy: choose highest-probability action

25. IF … THEN pass(Teammate)IF … THEN pass(Teammate)IF … THEN pass(Teammate)Learning an MLN PolicyFormulas for each action: Aleph (Srinivasan)w0= 1.1w1 = 0.9…Weights: Alchemy (U. Washington)

26. MLN Policy RulesExamples for transfer from 2-on-1 BreakAway to 3-on-2 BreakAwayIF angle(topRight, goalCenter, me) ≤ 70 timeLeft ≥ 98 distance(me, Teammate) ≥ 3 THEN pass(Teammate)IF distance(me, GoalPart) ≥ 36 distance(me, Teammate) ≥ 12 timeLeft ≥ 91 angle(topRight, goalCenter, me) ≤ 80THEN pass(Teammate)IF distance(me, GoalPart) ≥ 27 angle(topRight, goalCenter, me) ≤ 75 distance(me, Teammate) ≥ 9 angle(Teammate, me, goalie) ≥ 25THEN pass(Teammate)

27. MLN Policy ResultsMLN policy transfer from 2-on-1 BreakAway to 3-on-2 BreakAway

28. ILP rulesets can represent a policy by themselvesDoes the MLN provide extra benefit?Yes, MLN policies perform as well or betterMLN policies can include action-sequence knowledgeDoes this improve transfer?No, the Markov assumption appears to hold in RoboCupAdditional Experimental Findings

29. MLN transfer can improve reinforcement learningHigher initial performancePolicies transfer better than Q-functionsSimpler and more generalPolicies can transfer better than macros, but not alwaysMore detailed knowledge, risk of overspecializationMLNs transfer better than rulesetsStatistical-relational over pure relationalAction-sequence information is redundantMarkov assumption holds in our domain Conclusions

30. Future WorkRefinement of transferred knowledgeRevising weightsRelearning rules(Mihalkova et al. 2007) Too-specificclauseBetterclauseToo-generalclauseBetterclause

31. Future WorkProbabilityBin NumberRelational reinforcement learningQ-learning with MLN Q-functionPolicy search with MLN policies or macroMLN Q-functions lose too much information:

32. Co-author: Jude ShavlikGrantsDARPA HR0011-04-1-0007DARPA FA8650-06-C-7606Thank You