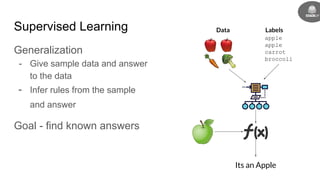
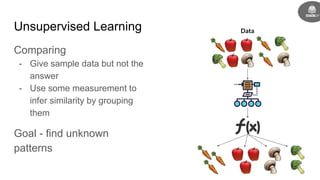
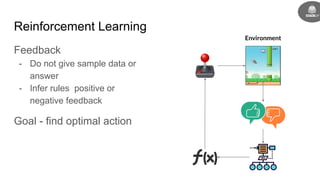
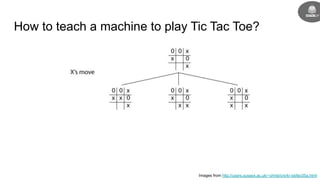
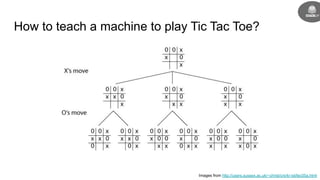
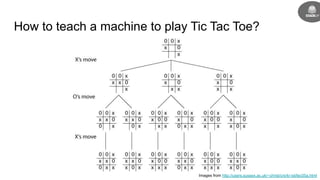
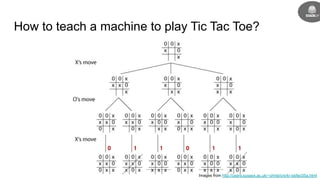
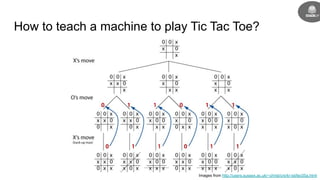
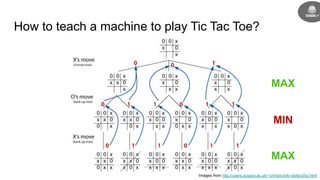
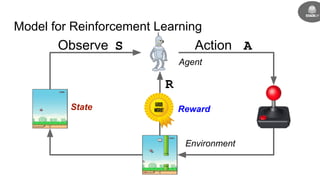
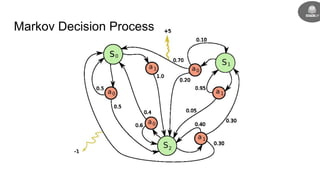
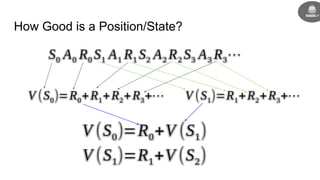
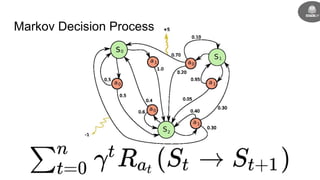
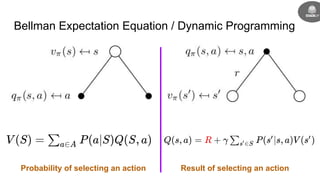
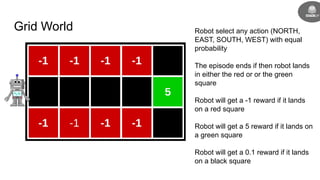
This document provides an introduction to reinforcement learning concepts including: - Reinforcement learning uses feedback to infer optimal actions without sample data or answers being provided directly. - It was inspired by Arthur Samuel programming the first machine to learn checkers in 1959 using a minimax algorithm. - Reinforcement learning problems can be modeled as Markov decision processes where an agent takes actions in an environment and receives rewards. 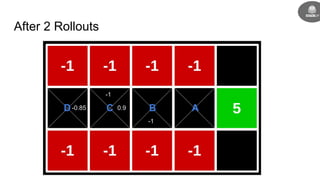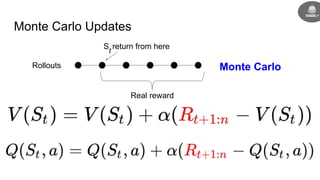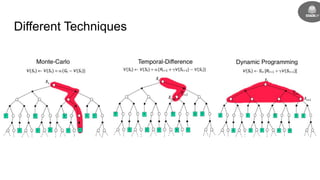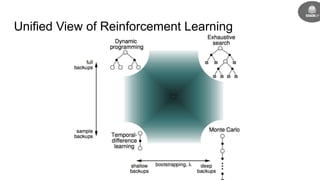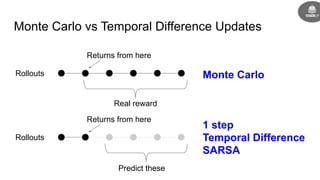- The goal is to learn a policy that maximizes long term rewards by estimating state and action values using techniques like Monte Carlo methods, temporal difference learning, and deep reinforcement learning.

1. Machine Learning
Dilbert from https://dilbert.com/strip/2013-02-02

2. Introduction to
Reinforcement Learning
Lee Chuk Munn
Slides at http://bit.ly/ld2019_rl

3. Objective
Introduce Major
Reinforcement Learning
Concepts

4. What is Machine Learning?
“Machine learning is the field of
study that gives computers the
ability to learn without being
explicitly programmed”
Arthur Samuel

5. Programmed vs Learnt

6. Supervised Learning
Generalization
- Give sample data and answer
to the data
- Infer rules from the sample
and answer
Goal - find known answers
apple
apple
carrot
broccoli
LabelsData
Its an Apple

7. Unsupervised Learning
Comparing
- Give sample data but not the
answer
- Use some measurement to
infer similarity by grouping
them
Goal - find unknown
patterns
Data

8. Reinforcement Learning
Feedback
- Do not give sample data or
answer
- Infer rules positive or
negative feedback
Goal - find optimal action
Environment

9. Wrote the first
program that learn
how to play
checkers in 1959
Uses the minimax
algorithm
Arthur Samuel

10. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

11. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

12. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

13. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

14. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

15. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html

16. How to teach a machine to play Tic Tac Toe?
Images from http://users.sussex.ac.uk/~christ/crs/kr-ist/lec05a.html
MAX
MIN
MAX

17. Model for Reinforcement Learning
ActionObserve
Agent
Environment
State Reward
S A
R

18. Markov Decision Process

19. How Good is a Position/State?

20. Central Idea of Any Autonomous Agent

21. Markov Decision Process

22. Bellman Expectation Equation / Dynamic Programming
Probability of selecting an action Result of selecting an action

23. Grid World Robot select any action (NORTH,
EAST, SOUTH, WEST) with equal
probability
The episode ends if then robot lands
in either the red or or the green
square
Robot will get a -1 reward if it lands
on a red square
Robot will get a 5 reward if it lands on
a green square
Robot will get a 0.1 reward if it lands
on a black square

24. First Iteration - State Value
AB
0.78-0.45-0.45-0.45
t = 0
CD

25. Second Iteration - State Value
0.66-0.4-0.68-0.68
0.78-0.45-0.45-0.45
t = 0
t = 1

26. State Value
We know how good it is to be in a
particular state viz. how close we are
to the goal
But how do we know what is the best
action to take so that we can land in
the next best state0.66-0.4-0.68-0.68
0.78-0.45-0.45-0.45
t = 0
t = 1

27. Action Value
Pick the best action
0.66-0.4-0.68-0.68
t = 1

28. First Iteration - Action Values
1.250.03
-0.25
-0.25
0.030.03
-0.25
-0.25
0.030.03
-0.25
-0.25
0.030.03
-0.25
-0.25

29. Second Iteration - Action Values
1.25-0.09
-0.25
-0.25
0.22
-0.25
-0.25
-0.09-0.09
-0.25
-0.25
-0.09-0.09
-0.25
-0.25
-0.09
Policy
emerging
after 2
iterations

30. Action Value
No way to make decision with state value
Keep the value of each action separate so we can select the best action
Treat this as an array of terms. max
behaves like Python max() function

31. When to Use What
Deterministic - as sure
as the sunrise
Minimax
Stochastic - as sure as
the weather forecast
MDP

32. What happens when you get end up in
a totally alien environment?

33. Law of Large Numbers - Monte Carlo
When you have no knowledge of the MDP (model free)
Sample forever, the probabilities will converge to their
true values
What should you wear?

34. Monte Carlo
Generate an episode using your current agent’s policy
Average the return for the first occurrence of (state, action) pair
(D,E) = (0.1 + -1 + 0.1 + 0.1 + -1) / 2 = -0.85
(C,N) = -1 / 1 = -1
(C,E) = (0.1 + -1) / 1 = 0.9
(B,S) = -1 / 1 = -1
Use the slightly better policy to generate another episode
0.1 -1
(D,E) (C,N)
0.1 0.1 -1
(D,E) (C,E) (B,S)
ABCD

35. After 2 Rollouts
-0.85
-1
0.9
-1
ABCD

36. Monte Carlo Updates
Rollouts
S
t
return from here
Real reward
Monte Carlo

37. Going to Alpha Centauri

38. Temporal Difference Updates
S
t
return from here
Rollouts
Predict these
1 step
Temporal Difference
SARSA

39. Different Techniques

40. Unified View of Reinforcement Learning

41. Demo

42. State/Action Value
Exact
- Dynamic Programming
Approximate
- Linear combination
- Neural net
- Etc.

43. Monte Carlo vs Temporal Difference Updates
Rollouts
Returns from here
Real reward
Monte Carlo
Rollouts
Returns from here
Predict these
1 step
Temporal Difference
SARSA

44. Incremental Mean
Does this
look
familiar?

45. Monte Carlo Update
Learning rate
State value of previous iteration
Slightly better state
value after update
Cumulative reward from n
to the end of episode
Episodic updates based on real returns

46. Temporal Difference TD(0)
Incremental updates based on bootstraps
One step reward plus predicted
reward from the next state

47. Difference Between MC and TD
Monte Carlo
Update policy at the end of
an episode
Works only in episodic
environment
High variance
Temporal Difference
Update policy a little after
every step
Works with incomplete
sequences/non-terminating
High bias

48. SARSA(0)
Incremental updates based on bootstraps
Uses action-values instead of
state value