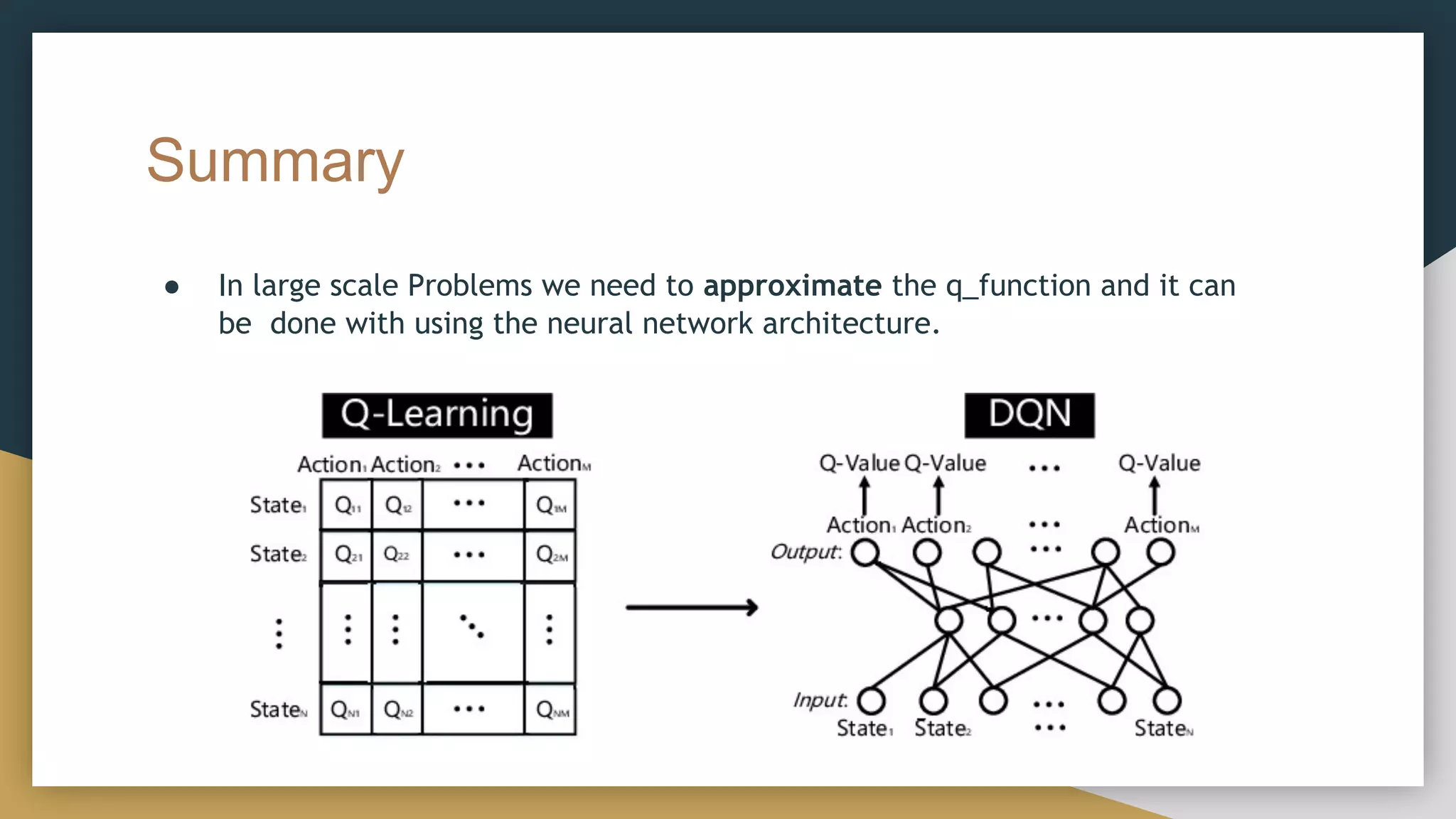
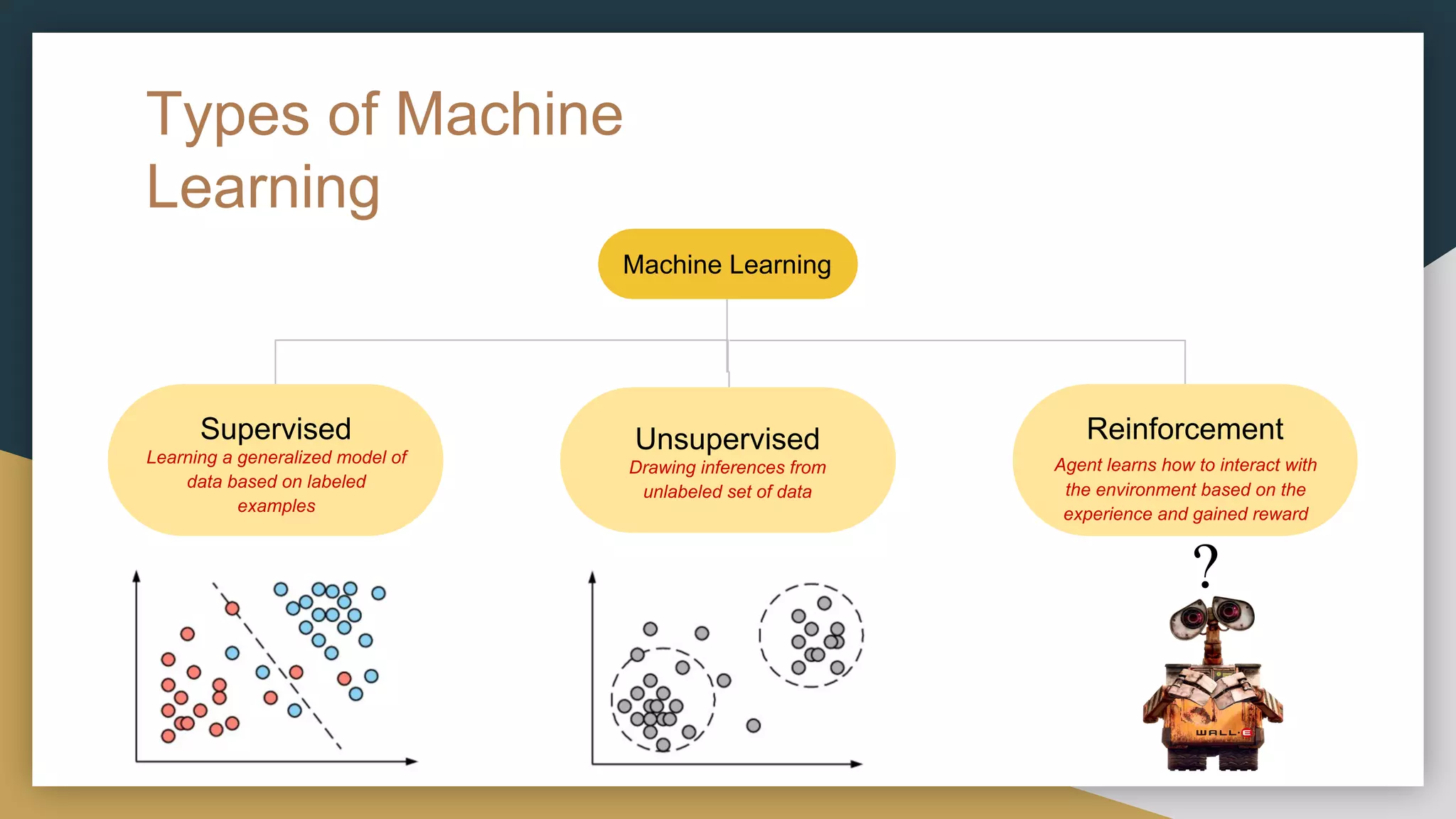
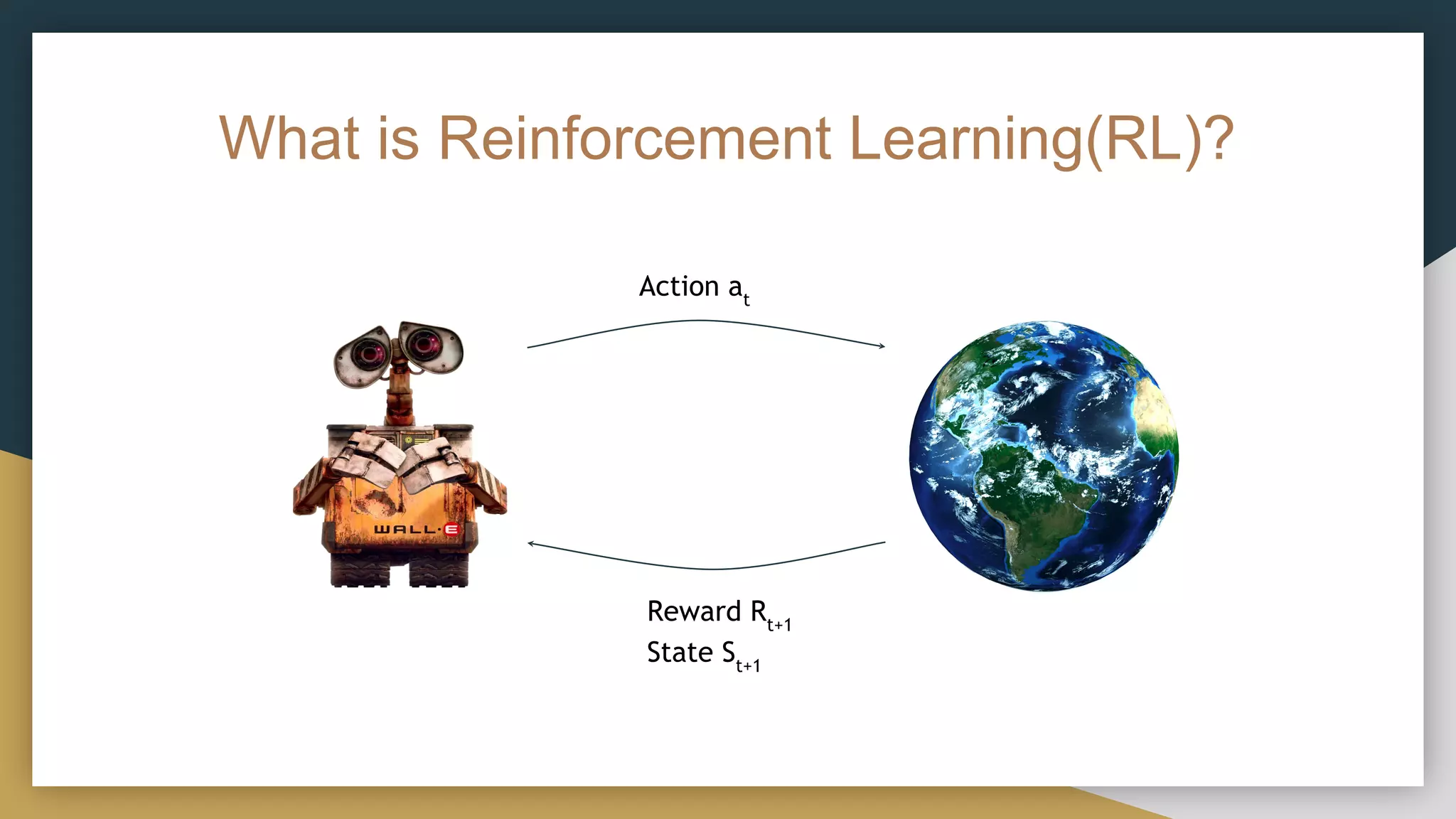
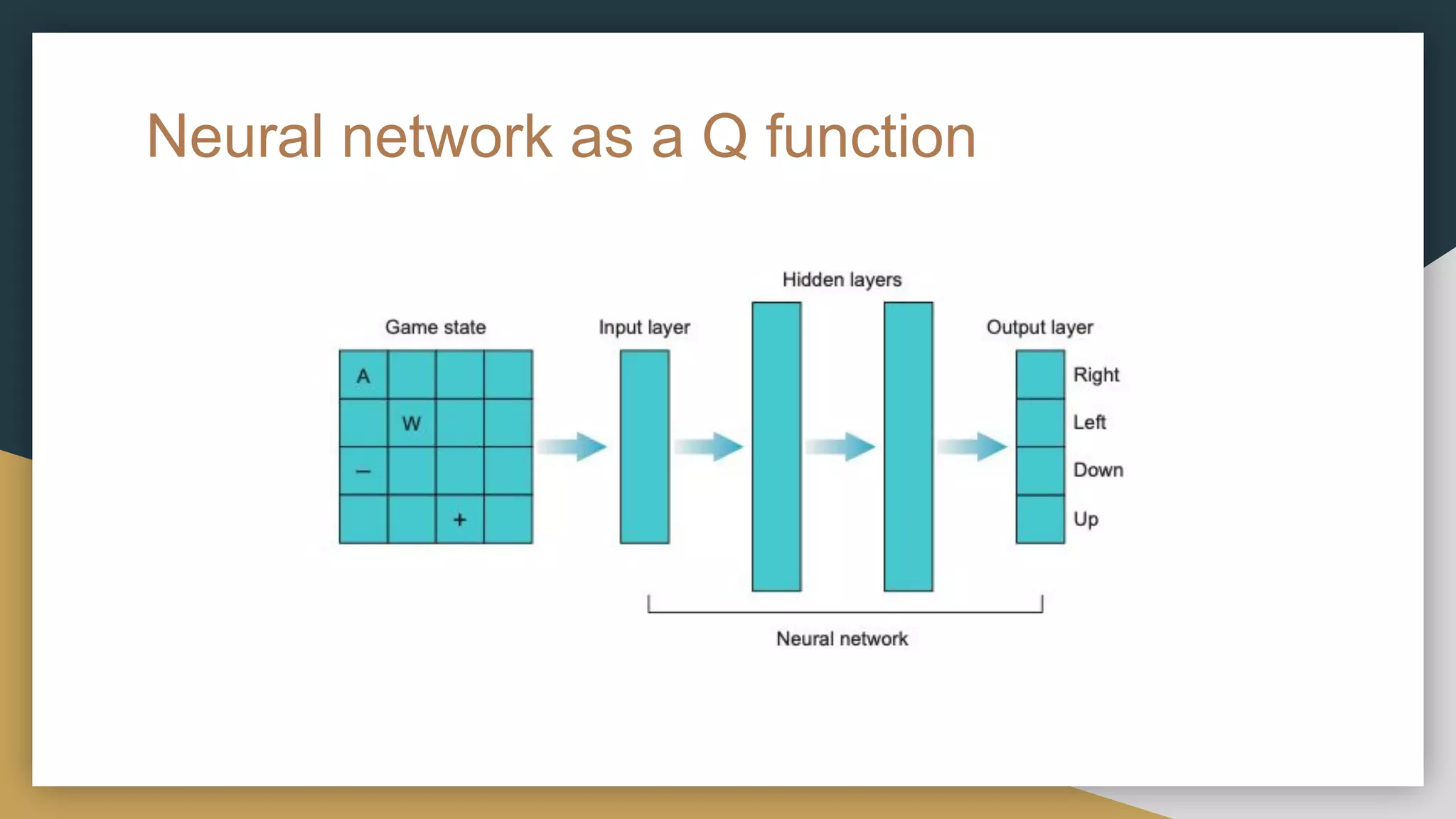
This document provides a comprehensive introduction to deep reinforcement learning (RL) and its foundational concepts, including types of machine learning, Markov processes, and different RL algorithms like Q-learning and policy iteration. It emphasizes the significance of maximizing cumulative rewards, explores the challenges posed by large state and action spaces, and discusses how neural networks can be used to approximate Q-functions in complex environments. The document also includes examples and strategies for problem-solving in RL contexts, such as exploration vs. exploitation in multi-armed bandit scenarios.

1. Introduction toDeep
Reinforcement Learning
By:
Reyhane Akhavan Kharazi
Mohammad Hossein Modirrousta

2. Types of Machine
Learning
Machine Learning
Supervised
Learning a generalized model of
data based on labeled
examples
Unsupervised
Drawing inferences from
unlabeled set of data
Reinforcement
Agent learns how to interact with
the environment based on the
experience and gained reward

3. What is Reinforcement Learning(RL)?
Action at
Reward Rt+1
State St+1

4. Example of RL
Agent start from the point (1, 1) and move on
to reach the Goal:
State = (1, 1)
Action = Right
new State = (1, 2)
reward = -1

5. Some definitions

6. Markov Process
● Markov Process or Markov Chain is a stochastic (random) process that satisfies Markov
property.
● Markov Property assume memorylessness, which means that predictions about the future of the
process can be made based only on the current state, without any knowledge about the historical
states.
● p(St+1
|S1
, … , St
) = p(St+1
|St
)

7. Markov Process
S0
S1
S3 S2
● Markov Process is characterized by:
○ States : The discrete states of a process at any time
○ Transition probability: The probability of moving from one state to another
0.4
0.6
0.5 0.5
0.3 0.7
S S′ P
S0
S1
0.6
S0
S0
0.4
S1
S2
0.5
S1
S3
0.5
S2
S2
0.7
S2
S3
0.3

8. Markov Reward Process(MRP)
● A Markov Reward Process or an MRP is a Markov
process with value judgment, saying how much reward
accumulated through some particular sequence that we
sampled.
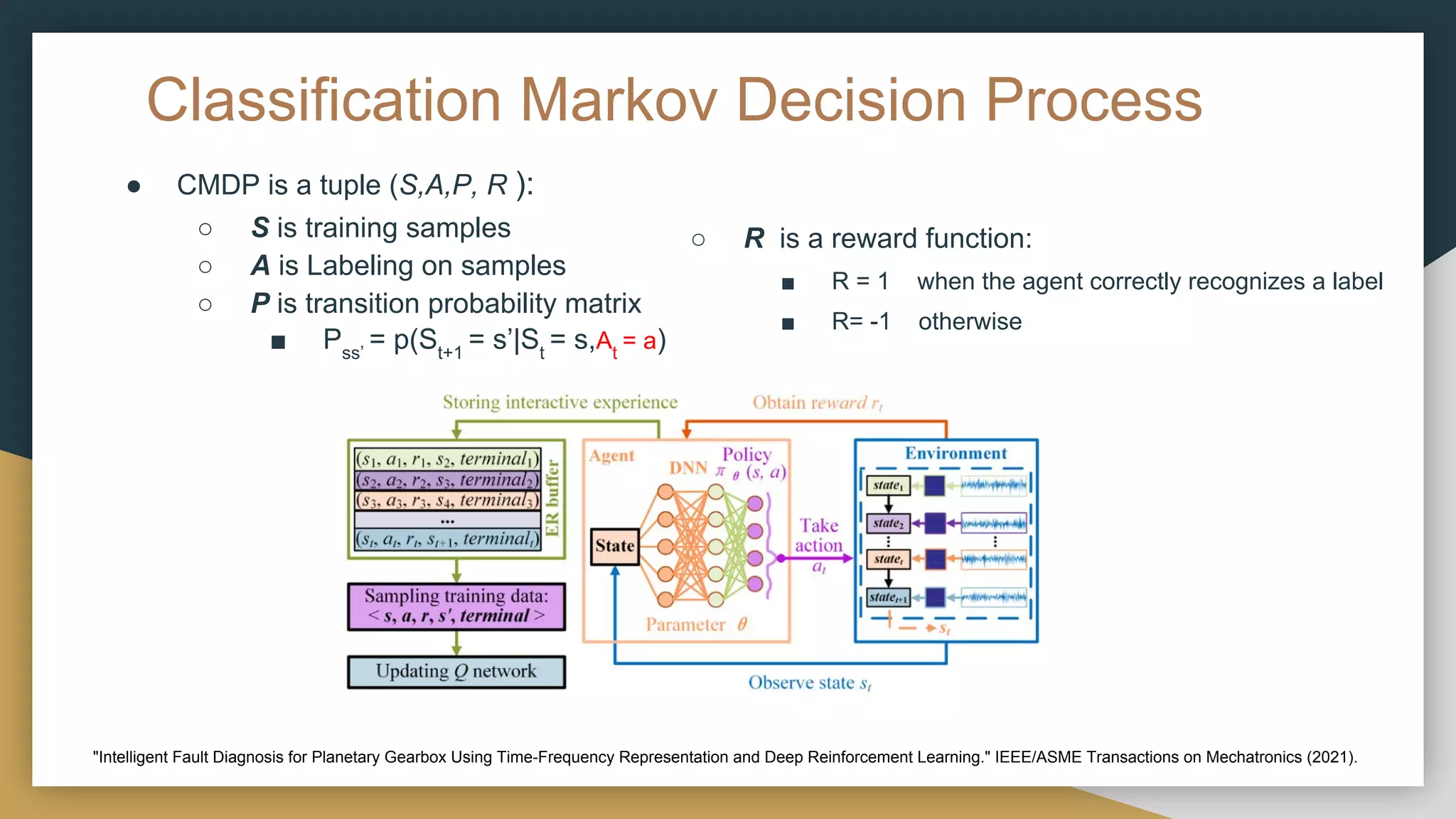
● MRP is a tuple (S, P, R, 𝛄):
○ S is finite set of states
○ P is transition probability matrix
■ Pss’
= p(St+1
= s’|St
= s)
○ R is a reward function:
■ Rs,a
= E [Rt+1
| St
= s]
■ It is immediate reward
○ 𝛄 is a discount factor, 𝛄 ∈ [0, 1]
0.4
S0
S1
S3 S2
0.6
0.5 0.5
0.3 0.7
R = -1 R = +2
R = -1
R = +5

9. Return
- Our goal is to maximize the return.
- The return Gt
is the total discount reward from time step t.
- The discount factor γ is a value between 0 and 1. If gamma is closer 0 it leads to
short sighted evaluation, while a value closer to 1 favors far sighted evaluation.

10. State Value
Function
State Value Function v(s): gives the long-term value of state s. It is the expected return
starting from state s

11. Value
Function
0.4
S0
S1
S3 S2
0.6
0.5 0.5
0.3
0.7
R = -1 R = +2
R = -1
R = +5

12. 0.4
0.5 0.5
-1 +2
-1
+5
0.6
0.5 0.5
-0.2 +4
-0.2
+5
0.3 0.7
v(s0
) = -1 + 1(0.4*-1 + 0.6*2) = -0.2
v(s1
) = 2 + 1(0.5*-1 + 0.5*5) = 4
v(s2
) = -1 + 1(0.7*-1 + 0.3*5) = -0.2
v(s3
) = +5
0.3 0.7
v(s0
) = -1 + 1(0.4*-0.2 + 0.6*4) = 1.32
v(s1
) = 2 + 1(0.5*-0.2 + 0.5*5) = 4.4
v(s2
) = -1 + 1(0.7*-0.2 + 0.3*5) = 0.36
v(s3
) = +5
0.4
0.6
0.5
0.7
0.3
0.5
3.66 5.33
1.66
+5
Value
Iteration
Iteration 0
0.4
0.6
Iteration 1 Final Iteration
…

13. Markov Decision Process(MDP)
● MDP can be represented as follows:
𝐬𝟎 → → 𝐬𝟏 → → 𝐬𝟐 → → ⋯
● MDP is a tuple (S, A, P, R, 𝛄):
○ S is finite set of states
○ A is finite set of actions
○ P is transition probability matrix
■ Pss’
= p(St+1
= s’|St
= s,At
= a)
○ R is a reward function:
s,a t+1 t t
■ R = E [R | S = s,A = a]
■ It is immediate reward
○ 𝛄 is a discount factor, 𝛄 ∈ [0, 1]
a r a r
a r
0 1 1 2
2 3
S0
S2
S1
S3
a0
a1
a2
0.5
0.5
0.6
0.4
1.0
R = -1
R = -1
R = +2
R = +5

14. Policy
A policy π is a distribution over actions given states. It fully defines the behavior of an agent.
MDP policies depend on the current state and not the history.

15. Value Function for
MDP
The state-value function vπ
(s) of an MDP is the expected return starting from state s, and
then following policy π.
State-value function tells us how good is it to be in state s by following policy π.

16. Action Value
Function
The action-value function qπ
(s, a) is the expected return starting from state s, taking action
a, and then following policy π.
Action-value function tells us how good is it to take a particular action from a particular state.
Gives us an idea on what action we should take at states.

17. Ways to solve
...
There are different ways to solve this problem.
● Policy Iteration, where our focus is to find optimal policy (model based)
● Value Iteration, where our focus is to find optimal value, i.e. cumulative reward (model
based)
● Q-Learning, where our focus is to find quality of actions in each state (model free)

18. Solving multi-armed bandit problem

19. Multi-arm Bandit
● A one-armed bandit is a simple slot machine wherein you insert a coin into the machine,
pull a lever, and get an immediate reward. (but in this lecture we assume this is free to test
each machine)
● In multi-armed bandit problem We have an agent which we allow to choose actions, and
each action has a reward that is returned according to a given, underlying probability
distribution. The game is played over many episodes (single actions in this case) and the
goal is to maximize your reward.

21. Exploration & Exploitation
● When we first start playing, we need to play the game and observe the rewards we get
for the various machines. We can call this strategy exploration, since we’re essentially
randomly exploring the results of our actions.
● There is a different strategy we could employ called exploitation, which means that we
use our current knowledge about which machine seems to produce the most rewards.
● Our overall strategy needs to include some amount of exploitation (choosing the best
lever based on what we know so far) and some amount of exploration (choosing
random levers so we can learn more).

22. Epsilon-greedy strategy
In epsilon-greedy strategy we choose the action based on some exploration and some
exploitation.
with a probability, ε, we will choose an action, a, at random, and the rest of the time
(probability 1 – ε) we will choose the best lever based on what we currently know from past
plays.

23. Solving the n-armed bandit
#Initialize the eps to balance the exploration and exploitation
eps = 0.2
for i in range(number_of_iterations):
if random.random() > eps:
# Exploitation: choose the best arm according to it's average reward
selected_arm = choose_the_best_arm()
else:
# Exploration: select an arm randomly
selected_arm = random_selection(number_of_arms)
# pull the selected arm and get the immediate reward
immediate_reward = get_reward(selected_arm)
# we should update the reward of the selected arm and add it to our history
update_mean_reward(selected_arm, immediate_reward)

24. Q-learning
“Q-learning is an off policy reinforcement learning
algorithm that seeks to find the best action to take given
the current state. It’s considered off-policy because the q-
learning function learns from actions that are outside the
current policy, like taking random actions, and therefore a
policy isn’t needed. More specifically, q-learning seeks to
learn a policy that maximizes the total reward.”

25. Q-learning
Q(St
,At
) : Prediction of model
Rt+1
+ 𝛄 max Q(St+1
,a) : Estimation of target value

26. Q-Learning Example
Q =
s1
s2
s3
Q′(s,a) = 3 + 0.01 * [Rt+1
+ 0.9 max Q(St+1
,a) - Q(St
,a)] = 3 + 0.01*[4 + 0.9*10 - 3] = 3.1
Assume we are in state s1
and we choose action a2. This action will take us to state s3.
The reward of env to our action is +4.
Learning rate = 0.01
Discounted factor = 0.9
a0
a1
a2
a3
a4
a5
a0
a1
a2
a3
a4
a5
s0 12 1 3 1 10 6 s0 12 1 3
1
10 6
0 1 3 0 1 2 Q′ =
s1 0 1 3.1 0 1 2
8 5 0 1 0 2 s2 8 5 0
1
0 2
0 1 3 9 0 10 s3 0 1 3
9
0 10

27. Large scale Reinforcement learning
● Reinforcement learning can be used to solve large problems
○ Backgammon: 1020
states
○ Go: 1070
states
○ Atari games, Helicopter, …
● So far we mostly considered lookup tables
○ Every state-action pair s, a has an entry q(s, a)
● Problem with large MDPs:
○ There are too many states & actions to store in memory
○ It is too slow to learn the value of each state individually
● Solution:
○ We need to approximate the Q function.

28. Q function
The original Q function accepts a state-action pair and returns the value of that state-action pair—a
single number.
DeepMind used a modified vector-valued Q function that accepts a state and returns a vector of
state-action values, one for each possible action given the input state. The vector-valued Q function
is more efficient, since you only need to compute the function once for all the actions.

29. Deep Q-learning : Building the network
● The last layer will simply produce an output vector of Q values—one for each possible action.
● In this lecture we use the epsilon-greedy approach for action selection.
● instead of using a static ε value, we will initialize it to a large value and we will slowly
decrement it. In this way, we will allow the algorithm to explore and learn a lot in the
beginning, but then it will settle into maximizing rewards by exploiting what it has learned.

30. Gridworld Example
The board of
game
This is how the Gridworld board is represented as a
numpy array.
Each matrix encodes the position of one of the four
objects: the player, the goal, the pit, and the wall.

31. Neural network as a Q function

32. Deep Q-learning
Algorithm
Initialize action-value function(weights of the network) with random
weights For episode = 1,M do:
Initialize the game and get starting state s
For t = 1,T do:
With probability ε select a random action at
; Otherwise select at
= maxa
Q(s, a)
Take action at
, and observe the new state s′ and reward rt+1
.
Run the network forward using s′. Store the highest Q value, which we’ll call maxQ = maxa
Q(s′,a)
if the game continues
rt+1
+ γ *maxQ
r
t+1
if the game is over
Train the model with this sample
=>
s = s′
If the game is over break; else continue
target value =
final_target = model.predict(state)
final_target[action] = target value
model.fit(state, final_target)

33. Double DQN and Dueling DQN
• Double DQN: Decouple selection and evaluation
• Dueling DQN: Split Q-value into advantage function and value function

34. Classification Markov Decision Process
● CMDP is a tuple (S,A,P, R ):
○ S is training samples
○ A is Labeling on samples
○ P is transition probability matrix
■ Pss’
= p(St+1
= s’|St
= s,At
= a)
■ R = 1 when the agent correctly recognizes a label
■ R= -1 otherwise
○ R is a reward function:
"Intelligent Fault Diagnosis for Planetary Gearbox Using Time-Frequency Representation and Deep Reinforcement Learning." IEEE/ASME Transactions on Mechatronics (2021).

35. Summary
●
●
● RL is a goal-oriented learning based on interaction with environment.
Gt
is the total discounted rewards from time step t. This is what we care about, the goal is to
maximize this return
The action-value function qπ
(s,a) is the expected return starting from state s, taking action a,
and then following policy π.
● The main idea of Q-learning is that your algorithm predicts the value of a state-action pair, and
then you compare this prediction to the observed accumulated rewards at some later time and
update the parameters of your algorithm, so that next time it will make better predictions.
● There are too many states and actions in large scale problems So we can not completely find the
optimal q-function.

36. Summary
● In large scale Problems we need to approximate the q_function and it can
be done with using the neural network architecture.

37. Resources
- https://www.youtube.com/watch?
v=2pWv7GOvuf0&list=PLqYmG7hTraZBiG_XpjnPrSNw-1XQaM_gB&ab_channel=DeepMin
d
- https://www.analyticsvidhya.com/blog/2017/01/introduction-to-reinforcement-learning
- implementation/
- https://www.youtube.com/playlist?list=PL2-dafEMk2A5FZ-MnPMpp3PBtZcINKwLA
- https://towardsdatascience.com/reinforcement-learning-demystified-markov-decision-
processes-part-1-bf00dda41690
- https://towardsdatascience.com/reinforcement-learning-an-introduction-to-the-concepts-
applications-and-code-ced6fbfd882d
- https://deeplizard.com/learn/video/QK_PP_2KgGE
- https://astrobear.top/2020/02/23/RLSummary6/

38. Thank
You