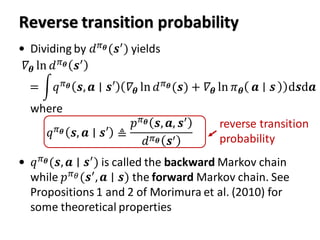
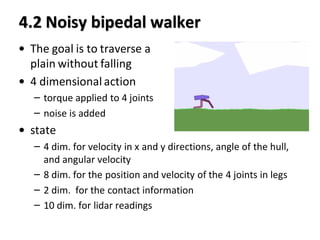
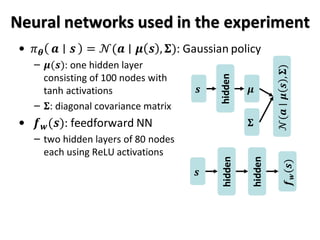
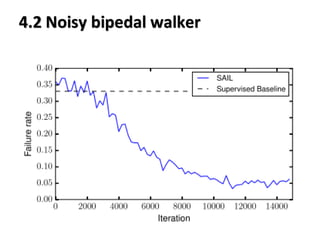
This paper proposes a method called State Aware Imitation Learning (SAIL) that aims to learn an imitation policy by reproducing both the demonstrated actions and visited states. SAIL formulates imitation learning as a maximum a posteriori problem, with one term aiming to reproduce the demonstrated actions and another term aiming to reproduce the demonstrated states by matching the policy's stationary distribution to the data distribution. The paper presents an online temporal difference learning algorithm to estimate the gradient of the log stationary distribution with respect to the policy parameters, which is needed to optimize the state reproduction term. The algorithm is demonstrated on a noisy bipedal walker domain, where SAIL is able to learn policies that traverse the environment without falling by imitating expert demonstrations