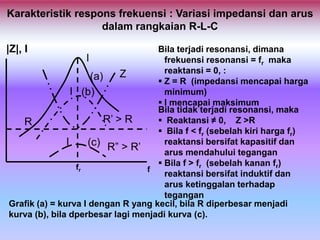
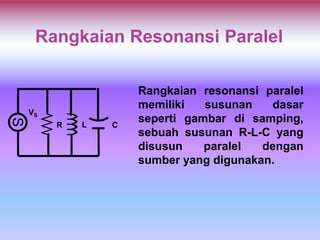
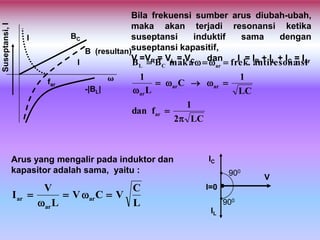
Dokumen ini membahas tentang rangkaian resonansi, termasuk definisi dan karakteristiknya dalam konteks rangkaian arus bolak-balik yang mengandung elemen induktor dan kapasitor. Ditekankan bahwa rangkaian dikatakan beresonansi ketika impedansinya sama dengan hambatan dan bagaimana hal ini mempengaruhi arus dan tegangan. Selain itu, faktor kualitas (Q) juga diperkenalkan sebagai ukuran selektivitas dari rangkaian resonator.

1. By: Nelly Sulistyorini
Rangkaian Elektrik 2
SARMAG Teknik Elektro 4
Gunadarma University
Rangkaian Resonansi
Paralel

2. Resonansi
Resonansi adalah suatu kondisi di mana rangkaian
dieksitasi dengan frekuensi naturalnya, ini
menyebabkan nilai |H(jω)| mencapai nilai minimum
dan maksimum.
Nilai |H(jω)| merupakan respon frekuensi yang
direpresentasikan sebagai perbandingan output
respon Y(jω) terhadap input sinusoidal X(jω) atau
yang lebih dikenal dengan fungsi transfer dan
domain jω:
Frekuensi yang menyebabkan kondisi tersebut
terjadi disebut dengan frekuensi resonansi (ω0), atau

3. Arti lain dari Resonansi
Resonansi adalah suatu gejala yang terjadi pada
suatu rangkaian arus bolak-balik yang
mengandung elemen induktor, L, dan kapasitor,
C.

4. Apa itu Rangkaian Resonansi ?
 Suatu rangkaian dikatakan beresonansi ketika
tegangan terpasang V dan arus yang dihasilkan I
berada dalam kondisi satu fasa.
Misalkan: ,
 Kita telah mempelajari bahwa XL dan Xc
bergantung pada frekuensi f dari arus bolak-balik
(AC). Jika XL=Xc, impedansi rangkaian Z menjadi
sama dengan hambatan R karena R tidak
bergantung pada f. Rangkaian yang memiliki nilai
seperti itu disebut dengan rangkaian resonansi.

5. Karakteristik respons frekuensi : Variasi impedansi dan arus
dalam rangkaian R-L-C
|Z|, I
R” > R’
(a)
(b)I
I
Z
I
R R’ > R
ffr
(c)
Bila terjadi resonansi, dimana
frekuensi resonansi = fr maka
reaktansi = 0, :
 Z = R (impedansi mencapai harga
minimum)
 I mencapai maksimum
Bila tidak terjadi resonansi, maka
 Reaktansi ≠ 0, Z >R
 Bila f < fr (sebelah kiri harga fr)
reaktansi bersifat kapasitif dan
arus mendahului tegangan
 Bila f > fr (sebelah kanan fr)
reaktansi bersifat induktif dan
arus ketinggalan terhadap
tegangan
Grafik (a) = kurva I dengan R yang kecil, bila R diperbesar menjadi
kurva (b), bila dperbesar lagi menjadi kurva (c).

6. Rangkaian Resonansi Paralel
Rangkaian resonansi paralel
memiliki susunan dasar
seperti gambar di samping,
sebuah susunan R-L-C yang
disusun paralel dengan
sumber yang digunakan.
S
R L C
VS

7. ADMITANSI, Y
Kebalikan dari impedansi Z adalah admitansi Y, atauKebalikan dari impedansi Z adalah admitansi Y, atau
Z
1
Y
Karena Z adalah bil. komplek maka Y juga bil. komplek :
Y = G + jB
Dengan G = Re Y disebut konduktansi
dan B = Im Y disebut suseptansi.
Satuan Y, G, dan B adalah Mho ( )
Ω
jXR
1
Z
1
jBGY


22
XR
jXR
jXR
jXR
.
jXR
1
jBG







khayalbagian
XR
X
B
nyatabagian
XR
R
G
:dengan
22
22





Jadi G tidak selalu sama dengan 1/R dan B tidak selalu sama

8. Bila frekuensi sumber arus diubah-ubah,
maka akan terjadi resonansi ketika
suseptansi induktif sama dengan
suseptansi kapasitif,
V =VR = VL = VC dan I = IR + IL + IC = Iar
LC2
1
fdan
LC
1
C
L
1
nsiantiresona.frekmakaBB
ar
arar
ar
arCL





L
C
VCV
L
V
I ar
ar
ar 


Arus yang mengalir pada induktor dan
kapasitor adalah sama, yaitu :
BC
-|BL|
B (resultan)
far
Suseptansi,I
I
I
ω
V
IC
IL
I=0
900
900

9. Faktor Kualitas (Q)
Definisi (dasar) dari Q:
Faktor kualitas merupakan ukuran selektivitas rangkaian resonator di mana
rangkaian resonator merupakan rangkaian filter BPF dengan lebar pita
(bandwith) sempit. Semakin besar nilai Q semakin sempit lebar pita
(bandwith).
Faktor Kualitas atau Q pada rangkaian paralel agak berbeda dengan Q pada
rangkaian seri.
Untuk harga RLC yang sama, atau
Untuk rangkaian paralel RLC:

10. Bandwith (BW) 3dB
Lebar bidang ditentukan oleh :
Lebar pita pada saat terjadi
level dayanya adalah ½ dari
daya maksimum.
Faktor kualitas dapat dinyatakan
sebagai perbandingan frekuensi
resonansi terhadap
bandwidth.
frekuensi resonansi f0 adalah rata-rata
geometri f1 dan f 2 :

11. Daftar Pustaka
 http://s3.amazonaws.com/ppt-download/iiirangkaianlistrikresonansi-
090312231147-
phpapp01.ppt?Signature=lshd44lQtchF%2Fa2DOzaw%2BE5dfVU%3D&Expires=1
288515798&AWSAccessKeyId=AKIAJLJT267DEGKZDHEQ (31 Oktober 2010
pukul 16.42)
 http://mujurrose.orgfree.com/1.ppt(8 November 2010 pukul 08.54)
 http://ocw.gunadarma.ac.id/course/computer-science-and-information/computer-
system-s1/listrik-magnet/karakteristik-rangkaian-rlc(8 November 2010 pukul
08.55)
 http://ocw.gunadarma.ac.id/course/computer-science-and-information/computer-
system-s1/listrik-magnet/karakteristik-rangkaian-rlc (8 November 2010 pukul
08.56)
 http://ilmu-elektronika.co.cc/index.php/arus-bolak-balik-ac/resonansi-pada-
rangkaian-ac.html(8 November 2010 pukul 08.58)
 http://www.ittelkom.ac.id/library/e-book/261206020220.pdf(8 November 2010
pukul 15.50)
 Soeparlan, Soepono & Yahdi, Umar.2007.Cerdas Belajar
Fisika.Bandung:Gunadarma