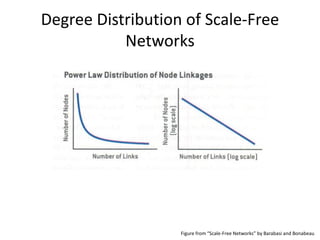
This document summarizes three common random graph models used to model complex real-world networks: Erdos-Renyi graphs, Watts-Strogatz small-world networks, and Barabasi-Albert scale-free networks. Erdos-Renyi graphs use a simple random edge placement process that can result in disconnected graphs or ones with small clustering. Watts-Strogatz networks address this by rewiring edges in a lattice, creating small-world properties but not realistic degree distributions. Barabasi-Albert networks use a preferential attachment mechanism where new nodes attach preferentially to higher degree nodes, producing power-law degree distributions seen in many real networks.

1. Random Graph Models
Network Science Reading Group
October 31, 2011

2. Modeling Complex Networks
• Real-world complex networks contain an
extremely large number of nodes (n)
• Nodes interact in various ways
– Capture interactions via a graph
– If two nodes interact, there is an edge between
them
• Question: How should edges be placed in
order to model real world complex networks?

3. Random Graph Models
• Look at three graph models that rely on a
“random” placement of edges
– Different initial conditions and probability
distributions lead to different types of graphs
• Three common models:
– Erdos-Renyi (Exponential)
– Watts-Strogatz (Small-World)
– Scale-Free/Barabasi-Albert (Power-Law
Distribution)

4. Erdos-Renyi
• Erdos-Renyi graph: G(n,p)
– n: number of nodes
– p: probability of adding an edge between any two
nodes
• Mechanism: each possible edge in the graph is
included with probability p
• What happens as n→∞ for various values of
p?

5. Phase Transitions
• If p < 1/n, graph contains many small components
• At p = 1/n, a giant component starts to form
• At p = log(n)/n, the graph is almost surely
connected
• There is a phase transition at 1/n
• Note that expected number of edges at each
node is (n-1)p

6. Characteristics of Erdos-Renyi Graphs
• If connected, average distance between two nodes is
small (small-world)
• Degree distribution is Poisson:
• Clustering coefficient: number of edges between
neighbors of a node, divided by total number of
possible edges between those neighbors
– Erdos-Renyi graphs tend to have small clustering
coefficients – do not match real world networks (high
coefficients)
Figure from “Scale-Free Networks” by Barabasi and Bonabeau

7. Watts-Strogatz (Small World) Model
• An effort to generate small-world networks with high
clustering coefficients
• Start with regular lattice and rewire each edge with a
certain probability p
• Small-world and high clustering coefficient, but degree
distribution does not match real-world networks
Figure from “Statistical Mechanics of Complex Networks” by Albert and Barabasi

8. Scale-Free Networks
• Real world networks display degree
distributions that have a power-law
distribution
P( k )  k 
• These are called power-law or scale-free
networks
• Previous random graph models do not
generate scale free networks

9. Preferential Attachment
• Start with a small group of nodes
• At each time-step, a new node comes in and
attaches to existing nodes
– Key point: prefer to attach to nodes that have a
higher degree
• Can show that this leads to a network that has
a scale-free distribution
– Contains hubs that connect to many nodes

10. Degree Distribution of Scale-Free
Networks
Figure from “Scale-Free Networks” by Barabasi and Bonabeau