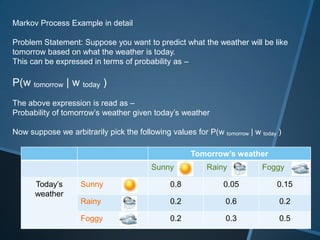
The document discusses Markov models, which are mathematical models used to predict dependent random events based on previously observed events. Specifically, it provides an example of using a Markov model to predict tomorrow's weather based on today's weather. Key aspects covered include the definition of a Markov process, examples of Markov and non-Markov systems, and calculating the probability of future weather events given the current weather.

1. Don’t you like to look at future sometimes?
Ashish Agarwal

2. Markov models are mathematical models based on the property of Markov
process
What is a Markov process?
Markov process analyzes a set of random, dependent events which depend
on what happened last.
e.g. 1. A Markov model could be to look at a long sequence of rainy, sunny &
foggy days in a particular region & try to predict what the weather will be
tomorrow.
e.g. 2. Tossing a coin that gathers a sequence of Heads & Tails & then tries to
predict what will appear next is NOT a Markov model because tossing a coin
to get a Head or a Tail are independent events.
Markov Models are applicable ONLY for dependent events.

3. Markov Process Example in detail
Problem Statement: Suppose you want to predict what the weather will be like
tomorrow based on what the weather is today.
This can be expressed in terms of probability as –
P(w tomorrow | w today )
The above expression is read as –
Probability of tomorrow’s weather given today’s weather
Now suppose we arbitrarily pick the following values for P(w tomorrow | w today )
Tomorrow’s weather
Sunny Rainy Foggy
Today’s Sunny 0.8 0.05 0.15
weather
Rainy 0.2 0.6 0.2
Foggy 0.2 0.3 0.5

4. Tomorrow’s weather
Sunny Rainy Foggy
Today’s weather Sunny 0.8 0.05 0.15
Rainy 0.2 0.6 0.2
Foggy 0.2 0.3 0.5
0.2
0.5
0.8
0.15
0.05 0.3 Finite State
0.2
0.2
Diagram
0.6

5. Question:
Given that today is Sunny (w1), what’s the probability that tomorrow is sunny (w2)
and the day after is rainy (w3)?
P( w2 = sunny, w3=rainy | w1 = sunny) = ?
The probability table (copied from previous slide)
Tomorrow’s weather
Sunny Rainy Foggy
Today’s weather Sunny 0.8 0.05 0.15
Rainy 0.2 0.6 0.2
Foggy 0.2 0.3 0.5
P( w2=sunny, w3=rainy | w1=sunny) = P (w2=sunny| w1=sunny) *
P (w3=rainy| w2=sunny, w1=sunny)
= 0.8 * 0.05
= 0.04

6. Where do we use Markov Models (MM)?
1. Speech Recognition
2. Bio Informatics
3. Face Expression Characterizations
4. Harry F. Olson at Bell Labs used MM to generate music by analyzing 11
songs of Foster