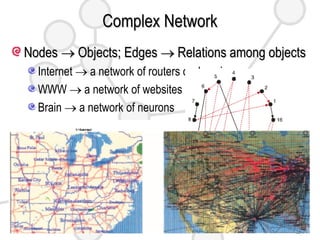
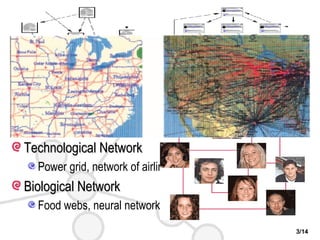
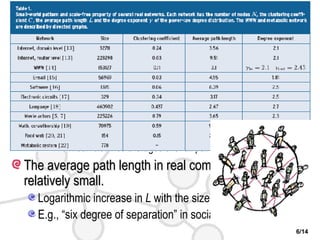
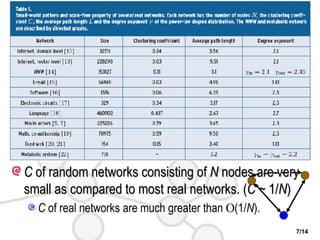
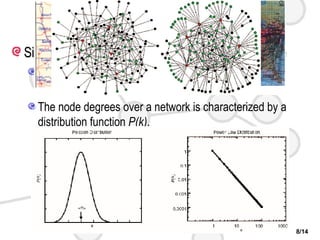
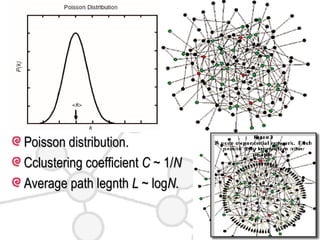
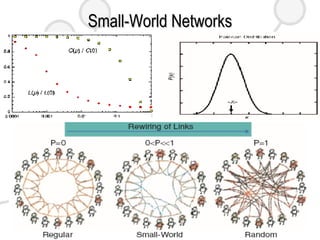
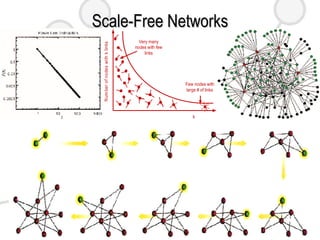
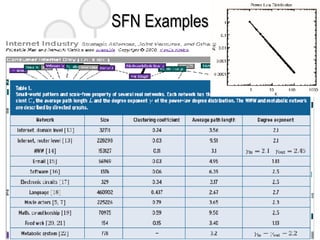
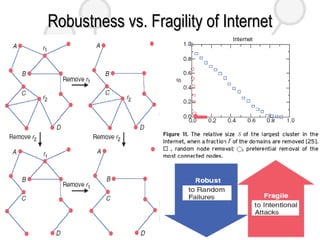
This document discusses complex networks such as social networks, technological networks, and biological networks. It finds that many complex networks exhibit small-world properties with short average path lengths between nodes, as well as scale-free properties with degree distributions that follow a power law. The document aims to characterize network structures, create models to explain properties like clustering and scale-freeness, and predict network behavior, such as resilience or disease transmission.

1. Complex Networks: Small-World, Scale-Free and Beyond 黃崇源

2. Complex Network Nodes  Objects; Edges  Relations among objects Internet  a network of routers or domains WWW  a network of websites Brain  a network of neurons Social Network, Sexual Network, Food Webs, Market, … Research Problems Diseases are transmitted through social networks. Computer viruses spread through the Internet. Energy is distributed through transportation networks

3. Types of Complex Networks Social Network Patterns of friendships between individuals Business relationships between companies Information Network WWW, citation network Technological Network Power grid, network of airline routes, roads and railways Biological Network Food webs, neural networks

4. Aims of Complex Network Theory Find global features that characterize the structure and behavior of networked systems. Local clustering, small-world, power-law properties, … Create network models to understand these properties. Random, small-world, scale-free networks, … Predict the behavior of networked systems. Network Resilience and robustness (WWW, sexual network) Epidemic Transmission Dynamics (SARS, Flu, HIV, …) Synchronization in Complex Dynamical Networks

5. Properties of Complex Networks Small-world effect Random, small-world, scale-free networks Local clustering Small-world network Degree distribution Normal distribution  random and small-world networks Power-Law distribution  scale-free network

6. Small-World Effect Definition The distance d ij between two nodes the number of edges along the shortest path connecting them. The network diameter, D The maximal distance among all distances d ij in the network. The average path length, L The mean distance averaged over all pairs of nodes. The average path length in real complex networks is relatively small. Logarithmic increase in L with the size of the network. E.g., “six degree of separation” in social network

7. Local Clustering Your friend’s friend is also your direct friend; or two of Your friends are quite possibly friends of each other. Node clustering coefficient c i = 2  E i / ( k i  ( k i – 1)) The average fraction of pairs of neighbors of a node that are also neighbors of each other. Network clustering coefficient C The average of ci over all node i. (0  C  1) C of random networks consisting of N nodes are very small as compared to most real networks. ( C ~ 1/ N ) C of real networks are much greater than  (1/ N ).

8. Degree Distribution Simplest and most important characteristic of node The node degree k i The total number of its connections. The node degrees over a network is characterized by a distribution function P(k) .

9. Complex Network Models Regular networks (e.g., Cellular Automata) Local clustering property Random networks (RNs) Small-world property Small-world networks (Watts and Strogatz’ SWNs) Local clustering and small-world properties Scale-free networks (SFNs) Small-world and power-law properties

10. Random Networks RN model Algorithm Starts with N nodes. Connects each pair of nodes with probability p. Creates a random networks with approximately pN ( N – 1) / 2 randomly placed links. Poisson distribution. Cclustering coefficient C ~ 1/ N Average path legnth L ~ log N.

11. Small-World Networks

12. Scale-Free Networks

13. SFN Examples

14. Robustness vs. Fragility of Internet