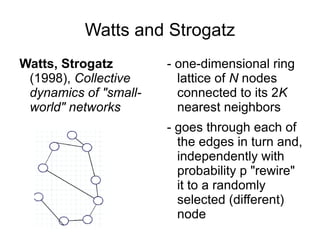
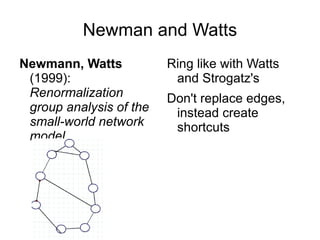
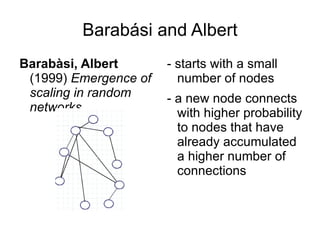
The document summarizes several random graph models: 1) Erdös and Renyi proposed connecting nodes with probability p, resulting in bell-shaped degree distributions. 2) Watts and Strogatz modeled small-world networks by rewiring edges in a ring lattice with probability p, finding short paths like social networks. 3) Barabasi and Albert grew networks by preferentially attaching new nodes to popular existing nodes, producing scale-free networks with power-law degree distributions and hubs.

1. Some random graphs for network models Birgit Plötzeneder

2. Bell-shaped node degree distributions

3. Random model Erdös,Renyi (1960s) On random graphs I; On the evolution of random graphs; On the strength of connectedness of a random grap h - start with N disconnected nodes - connect nodes with probability p to each other

4. Watts and Strogatz Watts, Strogatz (1998), Collective dynamics of "small-world" networks - one-dimensional ring lattice of N nodes connected to its 2 K nearest neighbors - goes through each of the edges in turn and, independently with probability p "rewire" it to a randomly selected (different) node

5. Watts and Strogatz - average distance grows like O(log(N) and not O(N). - support high levels of clustering „ The small-world effect (short average distance between nodes and high levelsof clustering) has been detected in networks that include a network of actors in Hollywood, the power generator network in the western US...“ Gerardo Chowell and Carlos Castillo-Chavez, Worst-Case Scenarios and Epidemics

6. Newman and Watts Newmann, Watts (1999): Renormalization group analysis of the small-world network model , Ring like with Watts and Strogatz's

7. Don't replace edges, instead create shortcuts

8. Power-law degree distributions = Pareto distributions

9. Pareto distributions - small number of highly connected nodes, most nodes have a small number of connections - Barabasi and Albert called them scale-free networks

10. Barabási and Albert Barabàsi, Albert (1999) Emergence of scaling in random networks - starts with a small number of nodes - a new node connects with higher probability to nodes that have already accumulated a higher number of connections

11. Klemm and Eguíluz " When a node is created it is linked to nodes that are popular at the time. It then receives links from nodes created subsequently, he said. "This continues until eventually the node under consideration loses its popularity." From: http://ifisc.uib-csic.es/victor/Nets/trn.html

12. Klemm, Eguíluz (2002) Growing scale-free networks with small-world behavior