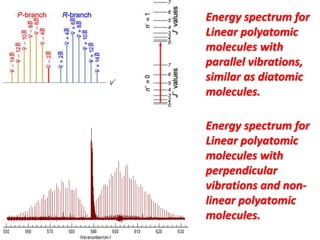
1) Vibrational spectra provides information about the molecular vibrations of a system by showing peaks that allow identification of components in a sample. Vibrational spectra can be seen in both diatomic and polyatomic molecules. 2) Polyatomic molecules have additional vibrational modes compared to diatomic molecules, including bond bending and asymmetric/symmetric stretching. Normal coordinates describe the coupled motion of atoms in a molecule as a linear combination of displacements. 3) Solving the coupled differential equations of motion results in normal modes of vibration, which are uncoupled simple harmonic motions characterized by normal frequencies and normal coordinates. This decoupling describes the overall motion of the coupled molecular system.

1. JAI NARAINVYAS UNIVERSITY
JODHPUR ( RAJ. )
MOLECULARANDRESONANCESPECTROSCOPY
SUBMITTEDTO– dr. s. l. meena
PRESENTEDBY – RAHUL MANSURIYA

2. VIBRATIONALSPECTRA,NORMAL
COORDINATESANDNORMAL
MODESOFVIBRATION

3. Vibrational Spectra
• Vibrational spectra provides information on the
molecular vibrations of a system in the form of a
vibrational spectrum, allowing identification of the
components present in the sample.
• As experimentally proved that a pure vibrational
spectra can be seen in only liquid molecules.

4. Vibrational Spectra Of Polyatomic
Molecules
• Vibrational spectra can be seen in diatomic and
polyatomic molecules. Most of discussion for
diatomic molecules will apply to polyatomic
molecules as well, but with 2 additions. One is the
larger number of vibrational degree of freedom,
and the other is the existence of other modes of
vibrations.
• For diatomic molecules, the only possible mode of
vibration is hand stretching, but the presence of
additional internal coordinates such as bond
bending, possible for polyatomic molecules.

5. Polyatomic molecules
We know that -
Degree of freedom = T + R + V = 3N
modes linear molecules nonlinear molecules
Translational 3 3
Rotational 2 3
Vibrational 3N-5 3N-6
Vibrational modes are of 2 types :
1. Stretching – (a) Symmetric (b) Asymmetric
2. Bending.

6. • For polyatomic molecules, vibrations are of 2 types :
(1) Parallel vibrations : Symmetric to principle axis.
(2) Perpendicular vibrations : Asymmetric to
principle axis.
• Polyatomic molecules :
For linear polyatomic molecules -
parallel vibrations perpendicular vibrations
selections rules : selection rules :
V = ± 1 V = ± 1
J = ± 1 J = 0, ± 1
P R branches. P Q R branches.

7. For non-linear polyatomic molecules –
for non linear molecules in both
cases of vibrations (parallel and perpendicular),
we always have P Q R branches.
selection rules –
V = ± 1
J = 0, ± 1
• We know that –
J = -1 for P branch
J = 0 for Q branch
J = + 1 for R branch

8. Energy spectrum for
Linear polyatomic
molecules with
parallel vibrations,
similar as diatomic
molecules.
Energy spectrum for
Linear polyatomic
molecules with
perpendicular
vibrations and non-
linear polyatomic
molecules.

9. NORMAL COORDINATES AND NORMAL
MODES
A normal coordinate is a linear combination of
Atomic cartesian displacement coordinates that
describe the coupled motion of all the items
that comprise a molecule. A normal mode is the
coupled motion of all the Atoms described by a
normal coordinate.
We can find the normal modes by equation of
motion or coupled differential equation of
motion.

10. Equation of motion/ coupled diffn eqn of motion –
mẍ1 + kx1 + k’(x1-x2) = 0
mẍ2 + kx2 - k’(x1-x2) = 0
Adding equation of motion –
2
𝑚 𝑑
𝑑𝑡2
(𝑥1 + 𝑥2)+ 𝑘 ( 𝑥1 + 𝑥2) = 0
𝑑2
𝑑𝑡2 (𝑥1 + 𝑥2 )+ 𝜔2
0 (𝑥1 + 𝑥2 )= 0
Subtracting equation of motion
2
𝑚 𝑑
𝑑𝑡2
(𝑥1 − 𝑥2 )+ (𝑘 + 2𝑘′) ( 𝑥1 − 𝑥2 ) = 0
𝑑2
𝑑𝑡2
(𝑥1− 𝑥2 )+ (𝜔2
0 + 2𝜔c
2) (𝑥1− 𝑥2 )= 0
Two new coordinates definition
𝑥1 + 𝑥2
𝑋1 =
2

11. 2
𝑥1 − 𝑥2
𝑋 = 2
𝑑2𝑋1
𝑑𝑡2
+ 𝜔1
2𝑋1 = 0
𝑑2𝑋2
𝑑𝑡2
+ 𝜔2
2𝑋2 = 0
We see that the motion of coupled system is now described by
two uncoupled differential equation, each of which
describe a simple harmonic motion of single frequency 𝜔1 and 𝜔2
in term of single coordinate ( X1 , X2 ). The solution of these eqns –
X1 = A1 cos (𝜔1𝑡 + ∅1 )
X2 = A2 cos (𝜔2𝑡 + ∅2)
These two simple hormonic motion obtained after decoupling
the coupled equation are called normal mode or simple modes.
Each modes of vibration has its normal frequency 𝜔1 and 𝜔2
and is described by coordinate ( X1 ,X2 ) known as normal
coordinate.

12. THANK YOU