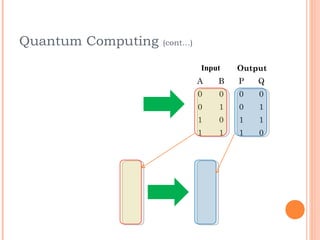
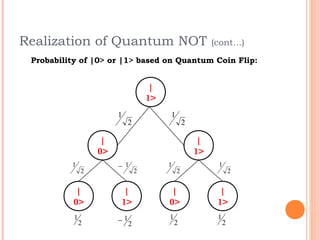
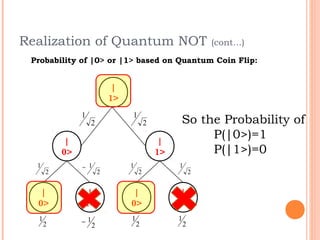
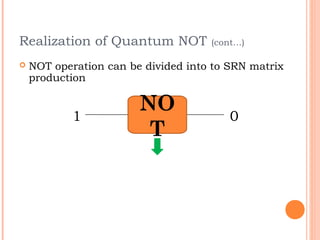
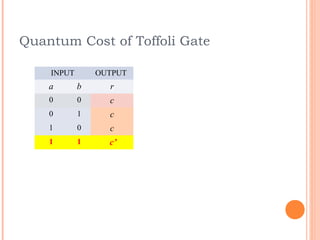
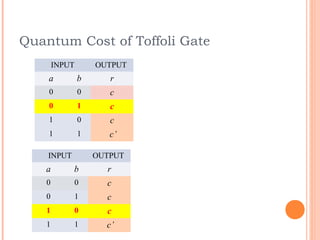
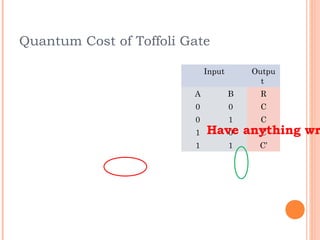
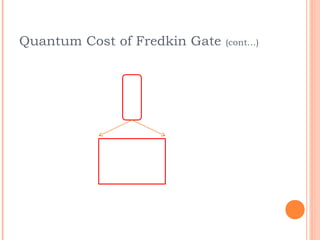
This document discusses the calculation of quantum cost for reversible circuits. It begins with an overview of reversible logic and quantum computing concepts like quantum gates. It then explains the realization of quantum NOT gate using quantum coin flips. Different quantum gates and their quantum costs are discussed, including Toffoli, Fredkin, Peres and NFT gates. Special cases involving quantum wires that have zero cost are also covered. The document concludes with an assignment to find the cost of additional gates and provides information about the author.

1. Quantum Cost Calculation of
Reversible Circuit
Sajib Mitra
Department of Computer Science and
Engineering
University of Dhaka
sajibmitra.csedu@yahoo.com

2. OVERVIEW
 Reversible Logic
 Quantum Computing
 Quantum Gates
 Realization of Quantum NOT
 Quantum wire and Special Cases
 Quantum Cost Calculation of RC
 Conclusion
 Assignment
 References

3. Reversible Logic
 Equal number of input and output vectors
 Preserves an unique mapping between input and output
vectors of the particular circuit
 One or more operation can implement in a single unit
called Reversible Gate
 (N x N) Reversible Gate has N number of inputs and N
number of outputs where N= {1, 2, 3, …}

4. Reversible Logic (cont…)
 Advantage
 Recovers bit-loss as well as production of heat
 Adaptable for Quantum Computing
 Multiple operations in a single cycle
 Uses low power CMOS technology

5. Reversible Logic (cont…)
 Limitation
 Feedback is strictly restricted
 Maximum and minimum Fan-out is always one

6. Reversible Logic (cont…)
Most Popular reversible gates are as follows:
Fig. 3x3 Dimensional Reversible gates

7. Reversible Logic (cont…)
Most Popular reversible gates are as follows:
Fig. 4x4 Dimensional Reversible gates

8. Quantum Computing
 First proposed in the 1970s, quantum computing relies on
quantum physics by taking advantage of certain quantum
physics properties of atoms or nuclei that allow them to work
together as quantum bits, or qubits, to be the computer's
processor and memory.
 Qubits can perform certain calculations exponentially faster
than conventional computers.
 Quantum computers encode information as a series of
quantum-mechanical states such as spin directions of
electrons or polarization orientations of a photon that might
represent as 0 or 1 or might represent a superposition of the
two values.
q =α 0 + β 1

9. Quantum Computing (cont…)
 Quantum Computation uses matrix multiplication rather than
conventional Boolean operations and the information
measurement is realized using qubits rather than bits The matrix
operations over qubits are simply specifies by using quantum
primitives as follows:

10. Quantum Computing (cont…)
Input Output Input/output Symbol
A B P Q Pattern
0 0 0 0 00 a
0 1 0 1 01 b
1 0 1 1 10 c
1 1 1 0 11 d

11. Quantum Computing (cont…)

12. Quantum Computing (cont…)
Input Output
A B P Q
0 0 0 0
0 1 0 1
1 0 1 1
1 1 1 0

13. Quantum Gates
Fig: Quantum Gates are used for realizing Reversible Circuit

14. Quantum Gates (cont…)
 What is SRN?
But

15. Quantum Gates (cont…)
 What is SRN?
But
NOT
But How?

16. Realization of Quantum NOT
Basic operator for single input line:
1. NOT
2. Coin Flip
3. Quantum Coin Flip

17. Realization of Quantum NOT (cont…)

18. Realization of Quantum NOT (cont…)
Probability of 0 or 1 based on Coin Flip:
1
1/2 1/2
0 1
1/2 1/2 1/2 1/2
0 1 0 1
1/4 1/4 1/4 1/4

19. Realization of Quantum NOT (cont…)
Probability of 0 or 1 based on Coin Flip:
1
1/2 1/2 So the Probability of
P(0)=1/2
0 1 P(1)=1/2
1/2 1/2 1/2 1/2
0 1 0 1
1/4 1/4 1/4 1/4

20. Realization of Quantum NOT (cont…)
Probability of |0> or |1> based on Quantum Coin Flip:
|
1>
1 1
2 2
| |
0> 1>
1 − 1 1 1
2 2 2 2
| | | |
0> 1> 0> 1>
1 −1 1 1
2 2 2 2

21. Realization of Quantum NOT (cont…)
Probability of |0> or |1> based on Quantum Coin Flip:
|
1>
1 1
2 2 So the Probability of
| |
P(|0>)=1
0> 1> P(|1>)=0
1 − 1 1 1
2 2 2 2
| | | |
0> 1> 0> 1>
1 −1 1 1
2 2 2 2

22. Realization of Quantum NOT (cont…)
 NOT operation can be divided into to SRN matrix
production
1
NO 0
T

23.  Quantum Cost (QC) of any reversible circuit is the
total number of 2x2 quantum primitives which are
used to form equivalent quantum circuit.

24. Quantum Wire and Special Cases (cont…)
Quantum XOR gate, cost is 1

25. Quantum Wire and Special Cases (cont…)
Two Quantum XOR gates, but cost is
0

26. Quantum Wire and Special Cases (cont…)
Quantum Wire

27. Quantum Wire and Special Cases (cont…)
Quantum Cost of V and V+ are same , equal to one.
SRN and its Hermitian Matrix on same
line.
VV+= Identity and the total cost = 0

28. Quantum Wire and Special Cases (cont…)
SRN and its Hermitian Matrix on same
line.
VV+= Identity and the total cost = 0

29. Quantum Wire and Special Cases (cont…)
The attachment of SRN (Hermitian Matrix of
SRN) and EX-OR gate on the same line
generates symmetric gate pattern has a cost
of 1.
Here T= V or V+

30. Quantum Wire and Special Cases (cont…)
The cost of all 4x4 Unitary Matrices (b, c, d) and the
symmetric gate pattern (e, f, g, h) are unit.

31. Quantum Cost of F2G

32. Quantum Cost of Toffoli Gate
But How?

33. Quantum Cost of Toffoli Gate
INPUT OUTPUT
a b r
0 0 c
0 1 c
1 0 c
1 1 c’

34. Quantum Cost of Toffoli Gate
INPUT OUTPUT
a b r
0 0 c
0 1 c
1 0 c
1 1 c’

35. Quantum Cost of Toffoli Gate
INPUT OUTPUT
a b r
0 0 c
0 1 c
1 0 c
1 1 c’
INPUT OUTPUT
a b r
0 0 c
0 1 c
1 0 c
1 1 c’

36. Now

37. Quantum Cost of Toffoli Gate
Input Outpu
t
A B R
0 0 C
0 1 C
1 Have anything wr
0 C
1 1 C’

38. Quantum Cost of Toffoli Gate
Input Outpu
t
A B R
0 0 C
0 1 C
1 0 C
1 1 C’
Ok

39. Quantum Cost of Toffoli Gate (cont…)
Alternate representation of Quantum circuit of TG…

40. Quantum Cost of Fredkin Gate
But How?

41. Quantum Cost of Fredkin Gate (cont…)

42. Quantum Cost of Fredkin Gate (cont…)

43. Quantum Cost of Fredkin Gate (cont…)

44. Quantum Cost of Fredkin Gate (cont…)

45. Quantum Cost of Fredkin Gate (cont…)

46. Quantum Cost of Fredkin Gate (cont…)

47. Quantum Cost of Peres Gate

48. Quantum Cost of NFT Gate

49. Quantum Cost of NFT Gate

50. Quantum Cost of MIG Gate

51. Assignment
Find out cost

52. About Author
Sajib Kumar Mitra is an MS student of Dept.
of Computer Science and Engineering,
University of Dhaka, Dhaka, Bangladesh. His
research interests include Electronics, Digital
Circuit Design, Logic Design, and Reversible
Logic Synthesis.

53. THANKS TO ALL