Automatski - RSA-2048 Cryptography Cracked using Shor's Algorithm on a Quantum Computer

CRACKING RSA-2048 USING
SHOR'S ALGORITHM ON A
QUANTUM COMPUTER
Automatski Solutions
http://www.automatski.com
E: Aditya@automatski.com , Founder & CEO
M: (904)-410-4617
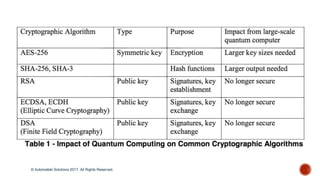
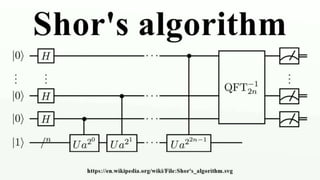
© Automatski Solutions 2017. All Rights Reserved.

WHAT IS A QUANTUM
COMPUTER?
 Its got something to do with Qubits, which unlike Bits are both 0 and 1 at the same
time
 They can do Gazillions of Calculations per second
 They can break all Existing Cryptography!

OUR PERCEPTION OF
QUANTUM COMPUTING???
Hmmm!
 Techcrunch
 Wall Street Journal, Economist,
Technology Review, Wired, Tech
Republic, Futurism, Forbes
 Medium/Blogs
 Youtube, Coursera, Udemy
 Conferences
 Magazines
 And…
 The Inhouse Expert!!!

Quantum computers are based on quantum mechanics !!!

AUTOMATSKI’S EFFORTS
(LAST 25 YEARS)
1. 25+ years of Fundamental Research
2. Solved 50-100 of the Toughest
Problems on the Planet considered
unsolvable in a 1000 years given the
current state of Human Capability
and Technology
3. Including 7 NP-Complete + 4 NP-
Hard Problems
4. Broke RSA 2048
5. … in 1990’s

AUTOMATSKI HISTORY &
TIMELINE

CONTEXT
 Quantum computing may still largely reside in the realm of scientists, but assuming it’s
too many years off to be relevant today would be a serious mistake.
 Research has largely exited the pure science phase and is now focusing on resolving
engineering challenges.
 But the real reason you should pay attention: quantum computing can – in theory –
defeat all modern encryption. From secure banking transactions to confidential
correspondence to, yes, Blockchain – quantum computing can crack them all quickly
and simply.
 Quantum Computing is well on its way to becoming cold hard reality, sooner than you
realize.

CONTEXT
 Any computer can easily multiply two large prime numbers together – but taking the
product of two such primes and factoring it is wicked hard. Such asymmetry is at the
core of all modern key-based encryption.
 Encrypting data is easy while decrypting them without the key could take years,
depending upon the length of the key.
 However, back in 1994, long before quantum computing was anything but pure theory,
mathematician and MIT professor Peter Shor created a quantum algorithm for
factoring large numbers far more quickly than conventional computers could.
 Shor’s Algorithm remains the bar every quantum computer aspires to.
 Today, we show that Shor’s algorithm, the most complex quantum algorithm known to
date, is realizable.

QUANTUM COMPUTING
TIMELINE

QUANTUM MECHANICS
(1990’S)

PAUL BENIOFF (QUANTUM
COMPUTING) (1986)

PETER W. SHOR’S
RESEARCH PAPER (1997)

GOOGLE’S 72 QUBIT
QUANTUM COMPUTER
(MARCH 2018)

QUANTUM COMPUTING @
AUTOMATSKI
1. 2014
1. 2048/4096 Universal Circuit Quantum
Computer Simulator v0.1
2. <Project put on hold due to funds>
2. 2018 (18/9/18)
1. Universal Adiabatic Quantum
Computer Simulator v1.0
2. Production Launch
3. Quantum Supremacy!!!
3. 2018 (27/9/18)
1. Special Purpose Quantum Annealing
Quantum Computer Simulator v1.0
4. December 2018
1. RSA-2048 Cracking Solution
5. December 2018
1. Universal Quantum Computations
with Quantum Walks

4 WAYS TO CRACK
1. P = NP (Theoretical Mathematics
& Computer Science)
2. Integer Factorization Algorithms
(Classical Algorithm’s, General
Number Field Sieve, etc.)
3. Quantum Computer Running
Shor’s Algorithm
4. Quantum Computer Simulator
Running Shor’s Algorithm

GENERAL NUMBER FIELD
SIEVE VS SHORS
 The largest factored RSA number is 232 decimal digits long (768 Bits)
 The most efficient known classical factoring algorithm, the general number field sieve, which works in
sub-exponential time
 Would take about 1023 operations would be necessary to factor RSA-230.
 Shor’s Algorithm works exponentially faster than this
 Shor’s algorithm could factor RSA-230 in about 3 million operations, and
 RSA-2048 in about 125,706,270 operations.
 RSA-4096 in about 553,377,825 operations, 4,947,802,324,992 quantum gates.

SHOR’S ALGORITHM

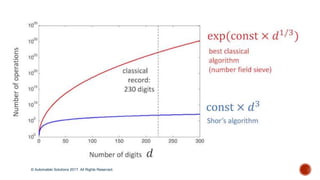
PROGRESS SO FAR
(CLASSICAL METHODS)
1. RSA-768 has 232 decimal digits (768 bits), and was factored on December 12, 2009
over the span of two years, by Thorsten Kleinjung, Kazumaro Aoki, Jens Franke, Arjen
K. Lenstra, Emmanuel Thomé, Pierrick Gaudry, Alexander Kruppa, Peter Montgomery,
Joppe W. Bos, Dag Arne Osvik, Herman te Riele, Andrey Timofeev, and Paul
Zimmermann.
 The CPU time spent on finding these factors by a collection of parallel computers amounted approximately
to the equivalent of almost 2000 years of computing on a single-core 2.2 GHz AMD Opteron-based
computer.
2. RSA-230 has 230 decimal digits (762 bits), and was factored by Samuel S. Gross at
Noblis, Inc. on August 15, 2018.
 In 2017, an analysis by a theory group led by Nike Dattani and experimental group led by Xinhua Peng and
Jiangfeng Du[35] determined that RSA-230 could be factored by a D-Wave quantum annealer if it had 687.5
MQB (mega-qubytes) or 5.5 billion qubits, much more than the 2048 qubits currently available on the largest
quantum annealer built to date. However, in the same paper they note that RSA-230 could simply be
factored by minimizing a 5893-variable quartic polynomial that takes in binary (0 or 1) input. Therefore a
quantum annealer with 5893 qubits that can be coupled together arbitrarily with each qubit coupled
simultaneously to at most three other qubits, would be able to factor RSA-230. The amount of time this
annealing would take is still an open question.

PROGRESS SO FAR (SHOR’S
ALGORITHM)
 In 2001, Shor's algorithm was
demonstrated by a group at IBM, who
factored 15 into 3 times 5, using an NMR
implementation of a quantum computer
with 7 qubits.
 In April 2012, the factorization of 143 = 11
times 13 was achieved, although this used
adiabatic quantum computation rather
than Shor's algorithm.
 In November 2014, it was discovered that
this 2012 adiabatic quantum computation
had also factored larger numbers, the
largest being 56153, (this number is equal
to 233 times 241.

WHERE ARE WE
GOING WITH ALL
THIS?

WE ARE GOING TO SHOW
YOU TODAY (LIVE)
 A Quantum Computer (Simulator)
 Simulator => Classical Simulation of a
Quantum Computer’s Quantum
Mechanics
 Which has The Capacity ( > 4096 Qubits)
to crack RSA 2048
 It has been available since 2014 CE.
 We have implemented the Shor’s
Algorithm on it.

MACHINES USED
 Development of Solution
 Machine #1
 AMD FX-6300 (6-Core), 32GB RAM
 Eight Year Old Machine
 Physical
 Testing of Parallelization & Concurrency
 Machine #2
 AWS EC2 m4.16xlarge ($3.2/hr)
 64 Core, 256 GB RAM
 Virtual Machine
 Machine #3
 AWS EC2 x1.32xlarge ($13.4/hr)
 128 Core, 1952 GB RAM
 Virtual Machine

BEFORE THE
A Message from our CFO!!!

MESSAGE FROM THE CFO!!!
 We are looking for Research & Development Grants
 Between
 $1m to $100m
 $1m will help us with the Research
 $100m will help us develop Path Breaking Solutions for over 10+ Domains using the
Breakthrough with a Big Bang.

AUTOMATSKI FUNDAMENTAL
RESEARCH
 Fundamental Research at Automatski has been working for the last 20-25+ years on
solving the toughest problems on the Planet.
 We have solved 7 NP-Complete Problems and 4 NP-Hard Problems, including the N-
Queens Completion Millennium Problem.
 We are applying them towards breakthroughs in 50+ Technology Domains
 These problems are considered unsolvable in a 1000 years given the current state of
Human Technology and Capability

SOLVED PROBLEMS
 N-Queens Completion
(Millennium Puzzle) Clay
Math Institute
 3-Sat/k-Sat
 Knapsack***
 Longest Common
Subsequence
 Travelling Salesman
Problem***
 3DM/nDM
 Graph Coloring -
Chromatic Number
 Linear Programming
 Integer Programming
 Mixed Integer
Programming
 Quadratic Programming
 Universal Expression
Programming
 Global Optimum in Hyper
Dimensional Space
 K-Means Clustering
 Universal Clustering
Algorithm
 Universal Constraint
Programming/Scheduling
 Integer Factorization***
 Prime Number Test***
 Universal Regression
 Non-Linear Random
Number Generation
 Automatic Theorem Proving
 Universal Experience
 Universal Heuristics
 Consciousness, Mind, Brain
 Genomics
 Billion & Trillion Actor Nano
Second Framework
 Universal Multi-Scale Simulations
 Internet Scale Rule Engine
 Internet Scale Workflow Engine
 Perfect Finance/Markets
 Perfect Environment
 Compromised All Cryptography
(RSA-2048, Elliptic Curve etc.)
 Post Quantum Cryptography
 Logarithmic Gradient Descent
Convergence
 Blackbox Function
Cracking/Reversal
 Hash Reversal (Incl. SHA-
256/512, LanMan etc.)
 NP-Complete Machine Learning
Algorithms (Clustering,
Regression, Classification)
 NP-Complete Deep Learning
Algorithms (ALL)
 Artificial General Intelligence
 Robotics (Simulations + RAD)***
 Universal Emotions
 Universal IQ
 Universal Creativity

FUND OUR RESEARCH
Together we can build the foundations of a better world

THE DEMO!

WHAT JUST HAPPENED?
 We used Shor’s Algorithm to Factorize some large numbers.
 This is exactly how cryptography like RSA, ECC etc. can be
cracked.
 This is how all Banking Systems, Internet Systems,
Blockchains can be compromised using Quantum Computers
 We used a Classical Simulation of a Quantum Computer with
more than 100,000+ Qubits.

OUR IMPLEMENTATION
 Is Multi-Threaded & Distributed (Internet Scale)
 Needs True Randomness to be more effective.
 Uses a Modest Constant RAM During Execution
Depending on the Problem Size
 Zero HDD Space Needed for computations.
 Linearly Scales - Horizontally (More Machines) 1000X
 Linearly Scales - Vertically (More Cores’) 10X
 Converting to C++ will accelerate it by 100X
 GPGPU will accelerate by 100X
 Custom ASIC & FPGA's will accelerate 1000X

HENCE…
 Using Shor’s Algorithm we can crack RSA-2048 in about 125,706,270
operations.
 That can be done really fast if we deploy our Solution on a Cloud with
100-500 machines
 All this is possible today!
 So basically, from where we stand RSA 2048 is Cracked!
 Yet Again!
 For the Nth time using N different schemes. Recall…
 P = NP !!!
 7 NP-Complete & 4 NP-Hard Problems Solved in Polynomial time
 N-Queens Completion etc. Including K-Means
 Quantum Computing
 Other Schemes…
 Integer Factorization
 K-SAT
 …

CONCLUSION & HEADLINES
 This “Proves” 4 things exactly
1. Quantum Computers based on Quantum
Mechanics Deliver on their Promise
2. Automatski’s Quantum Computer Simulator(s)
(3 types Circuit, Adiabatic, Annealing) with
100,000+ Qubits … are hence proven.
3. Shor’s Algorithm Delivers on its Promise.
4. All Existing Cryptography ‘is hereby’ cracked. It
‘can’ be and ‘will’ be cracked by Automatski’s
Customers of this Solution.

AVAILABLE
CONFIGURATIONS
 RSA – 100 (US$ 100m/license/year)
 RSA – 2048 (US$ 1bn/license/year)
 RSA – 4096 (US$ 2bn/license/year)
 Bigger??? (Contact us)
*** Plus Compute + Storage + Network
Costs

FROM HERE…
 RSA Cracker
 Gen 1 (2018)
 Gen 2 (2019)
 Gen 3 (2019)
 Gen 4 (2020)
 Gen 5 (2020)
 Gen 6 (2021)
 Gen 7 (2022)
 In the future video’s you will see
 Universal Quantum Computations with Quantum Walks
 General/Arbitrary NP-Complete – K-SAT in Polynomial Time O(N2).
 A Deterministic Algorithm to Find the Global Optima in a Billion Dimensions/Variables.
 I’m sure you will find it very interesting!!!

DO YOU HAVE ANY IDEA?
 What we can do with all the things
Automatski is demo’ing?
 Even though we have just shown
everyone 3-4 out of a 100+
Inventions and Innovations?
 Can you put a $ value on it? How
much will it be? Millions? Billions?
Trillions???
 Any guesses? Wanna try???

THIS MEANS TRILLIONS OF
DOLLARS!!!

NEXT STEPS FOR
PROSPECTIVE CUSTOMERS
 Please contact sales at info@automatski.com
 Send an email with the following information…
 What is the problem(s) you are trying to solve?
 We will take it from there…
*** No Free Trials/Pilots/POCs Offered

WARNING!!!
 Don’t contact us asking for The Source Code
 Don’t contact us asking us to
 File Patents
 Make Public Disclosures of our Algorithm(s)
 Publish Academic Papers

SAMPLE PROBLEMS &
RESULTS
 The .Zip File Contains
1. Sample Problems
2. And their Solutions
 Download .Zip File here
 http://bit.ly/2Ek0Xjs
 Download this Presentation here
 http://bit.ly/2G8rWju
Search Youtube for “Automatski Solutions”
To See The Video Recording of The Demo

THANKYOU!

SECURITY STRENGTH (BITS)
VS KEY SIZES

GROVERS’ – QUANTUM
RESOURCES

SHORS’ – QUANTUM
RESOURCES

CIRCUIT DEPTH

REFERENCES
 P. Shor, Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer,SIAM
J.Sci.Statist.Comput.26 (1997) 1484
 L. M. Adleman (1994), Algorithmic number theory—The complexity contribution, in Proceedings of the 35th Annual Symposium on
Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, CA, pp. 88–113.
 L. M. Adleman and K. S. McCurley (1995), Open problems in number-theoretic complexity II, in Proceedings of the 1994 Algorithmic
Number Theory Symposium, Ithaca, NY, May 6–9, Lecture Notes in Computer Science, L. M. Adleman and M.-D. Huang, eds.,
Springer, to appear.
 A. Barenco, C. H. Bennett, R. Cleve, D. P. DiVincenzo, N. Margolus, P. Shor, T. Sleator,
 J. A. Smolin, and H. Weinfurter (1995a), Elementary gates for quantum computation, Phys. Rev. A, 52, pp. 3457–3467.
 A. Barenco, D. Deutsch, A. Ekert, and R. Jozsa (1995b), Conditional quantum dynamics and logic gates, Phys. Rev. Lett., 74, pp.
4083–4086.
 P. Benioff (1980), The computer as a physical system: A microscopic quantum mechanical Hamilto- nian model of computers as
represented by Turing machines, J. Statist. Phys., 22, pp. 563–591.
 (1982a), Quantum mechanical Hamiltonian models of Turing machines, J. Statist. Phys., 29, pp. 515–546.
 (1982b), Quantum mechanical Hamiltonian models of Turing machines that dissipate no energy, Phys. Rev. Lett., 48, pp. 1581–1585.
 C. H. Bennett (1973), Logical reversibility of computation, IBM J. Res. Develop., 17, pp. 525–532.
 (1989), Time/space trade-offs for reversible computation, SIAM J. Comput., 18, pp. 766–776.
 C. H. Bennett, E. Bernstein, G. Brassard, and U. Vazirani (1994), Strengths and weaknesses of quantum computing, preprint.

REFERENCES
 C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J. A. Smolin, and W. K. Wooters (1995), Purification of noisy entanglement, and faithful
teleportation via noisy channels, Phys. Rev. Lett., to appear.
 E. Bernstein and U. Vazirani (1993), Quantum complexity theory, in Proceedings of the 25th Annual ACM Symposium on Theory of Computing, ACM, New
York, pp. 11–20.
 A. Berthiaume and G. Brassard (1992a), The quantum challenge to structural complexity theory, in Proceedings of the Seventh Annual Structure in
Complexity Theory Conference, IEEE Computer Society Press, Los Alamitos, CA, pp. 132–137.
 (1992b), Oracle quantum computing, in Proceedings of the Workshop on Physics of Computation: PhysComp ’92, IEEE Computer Society Press, Los Alamitos, CA, pp.
195–199.
 A. Berthiaume, D. Deutsch, and R. Jozsa (1994), The stabilisation of quantum computations, in Proceedings of the Workshop on Physics of
Computation: PhysComp ’94, IEEE Computer Society Press, Los Alamitos, CA, pp. 60–62.
 M. Biafore (1994), Can quantum computers have simple Hamiltonians, in Proceedings of the Workshop on Physics of Computation: PhysComp ’94, IEEE
Computer Society Press, Los Alamitos, CA, pp. 63–68.
 D. Boneh and R. J. Lipton (1995), Quantum cryptanalysis of hidden linear functions, Advances in Cryptology—CRYPTO ’95, Proceedings of the 15th Annual
International Cryptology Conference, Santa Barbara, CA, Aug. 27–31, D. Coppersmith, ed. Springer, pp. 424–437.
 J. F. Canny and J. Reif (1987), New lower bound techniques for robot motion planning problems, in Proceedings of the 28th Annual Symposium on
 J. Choi, J. Sellen, and C.-K. Yap (1995), Precision-sensitive Euclidean shortest path in 3-space, in Proceedings of the 11th Annual Symposium on
Computational Geometry, ACM, New York, pp. 350–359.
 I. L. Chuang, R. Laflamme, P. W. Shor, and W. H. Zurek (1995), Quantum computers, factoring and decoherence, Science, 270, pp. 1635–1637.
 I. L. Chuang and Y. Yamamoto (1995), A simple quantum computer, Phys. Rev. A, 52, pp. 3489–3496.

REFERENCES
 A. Church (1936), An unsolvable problem of elementary number theory, Amer. J. Math., 58, pp. 345– 363.
 J. I. Cirac and P. Zoller (1995), Quantum computations with cold trapped ions, Phys. Rev. Lett., 74, pp. 4091–4094.
 R. Cleve (1994), A note on computing Fourier transforms by quantum programs, preprint.
 D. Coppersmith (1994), An approximate Fourier transform useful in quantum factoring, IBM Research Report RC 19642.
 D. Deutsch (1985), Quantum theory, the Church–Turing principle and the universal quantum computer, Proc. Roy. Soc. London Ser. A, 400, pp. 96–117.
 (1989), Quantum computational networks, Proc. Roy. Soc. London Ser. A, 425, pp. 73–90.
 D. Deutsch, A. Barenco, and A. Ekert (1995), Universality of quantum computation, Proc. Roy. Soc. London Ser. A, 449, pp. 669-677.
 D. Deutsch and R. Jozsa (1992), Rapid solution of problems by quantum computation, Proc. Roy. Soc. London Ser. A, 439, pp. 553–558.
 D. P. DiVincenzo (1995), Two-bit gates are universal for quantum computation, Phys. Rev. A, 51, pp. 1015–1022.
 A. Ekert and R. Jozsa (1995), Shor’s quantum algorithm for factorising numbers, Rev. Mod. Phys., to appear.
 R. Feynman (1982), Simulating physics with computers, Internat. J. Theoret. Phys., 21, pp. 467–488.
 (1986), Quantum mechanical computers, Found. Phys., 16, pp. 507–531. Originally appeared in Optics News (February 1985), pp. 11–20.
 E. Fredkin and T. Toffoli (1982), Conservative logic, Internat. J. Theoret. Phys., 21, pp. 219–253.
 D. M. Gordon (1993), Discrete logarithms in GF(p) using the number field sieve, SIAM J. Discrete Math., 6, pp. 124–139.

REFERENCES
 G. H. Hardy and E. M. Wright (1979), An Introduction to the Theory of Numbers, Fifth ed., Oxford University Press, New York.
 J. Hartmanis and J. Simon (1974), On the power of multiplication in random access machines, in Proceedings of the 15th Annual Symposium on
Switching and Automata Theory, IEEE Computer Society, Long Beach, CA, pp. 13–23.
 A. Karatsuba and Yu. Ofman (1962), Multiplication of multidigit numbers on automata, Dokl. Akad. Nauk SSSR, 145, pp. 293–294 (in Russian). English
translation in Sov. Phys. Dokl., 7 (1963), pp. 595–596.
 D. E. Knuth (1981), The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, Second ed., Addison-Wesley.
 E. Knill (1995), personal communication.
 R. Landauer (1995a), Is quantum mechanics useful ? Philos. Trans. Roy. Soc. London Ser. A, to appear.
 (1995b), Is quantum mechanically coherent computation useful ? in Proceedings of the Drexel-4 Symposium on Quantum Nonintegrability—Quantum Classical
Correspondence, D. H. Feng and B-L. Hu, eds., International Press, to appear.
 Y. Lecerf (1963), Machines de Turing réversibles. Récursive insolubilité en n ∈ N de l’équation u = θnu, ou` θ est un isomorphisme de codes,
C. R. Acad. Française Sci., 257, pp. 2597–2600.
 A. K. Lenstra and H. W. Lenstra, Jr., eds. (1993), The Development of the Number Field Sieve,
 Lecture Notes in Mathematics, Vol. 1554, Springer.
 A. K. Lenstra, H. W. Lenstra, Jr., M. S. Manasse, and J. M. Pollard (1990), The number field sieve, in Proceedings of the 22nd Annual ACM Symposium on
Theory of Computing, ACM, New York, pp. 564–572. An expanded version appeared in Lenstra and Lenstra [1993], pp. 11–42.
 R. Y. Levine and A. T. Sherman (1990), A note on Bennett’s time-space tradeoff for reversible computation, SIAM J. Comput., 19, pp. 673–677.

REFERENCES
 S. Lloyd (1993), A potentially realizable quantum computer, Science, 261, pp. 1569–1571.
 (1994), Envisioning a quantum supercomputer, Science, 263, p. 695.
 (1995), Almost any quantum logic gate is universal, Phys. Rev. Lett., 75, pp. 346–349.
 N. Margolus (1986), Quantum computation, Ann. New York Acad. Sci., 480, pp. 487–497.
 (1990), Parallel quantum computation, in Complexity, Entropy and the Physics of Information, Santa Fe Institute Studies in the Sciences of Complexity, Vol. VIII, W. H.
Zurek, ed., Addison- Wesley, pp. 273–287.
 G. L. Miller (1976), Riemann’s hypothesis and tests for primality, J. Comput. System Sci., 13, pp. 300– 317.
 A. M. Odlyzko (1995), personal communication.
 G. M. Palma, K.-A. Suominen, and A. K. Ekert (1995), Quantum computers and dissipation, Proc. Roy. Soc. London Ser. A,
submitted.
 A. Peres (1993), Quantum Theory: Concepts and Methods, Kluwer Academic Publishers.
 C. Pomerance (1987), Fast, rigorous factorization and discrete logarithm algorithms, in Discrete Algo- rithms and Complexity,
Proceedings of the Japan–US Joint Seminar, June 4–6, 1986, Kyoto, D. S. Johnson, T. Nishizeki, A. Nozaki, and H. S. Wilf, eds.,
Academic Press, pp. 119–143.
 E. Post (1936), Finite combinatory processes. Formulation I., J. Symbolic Logic, 1, pp. 103–105.
 R. L. Rivest, A. Shamir, and L. Adleman (1978), A method of obtaining digital signatures and public-key cryptosystems, Comm.
Assoc. Comput. Mach., 21, pp. 120–126.
 L. A. Rubel (1989), Digital simulation of analog computation and Church’s thesis, J. Symbolic Logic, 54, pp. 1011–1017.

REFERENCES
 A. Scho¨nhage (1982), Asymptotically fast algorithms for the numerical multiplication and division of polynomials with complex
coefficients, in Computer Algebra EUROCAM ’82, Lecture Notes in Computer Science, Vol. 144, J. Calmet, ed., Springer, pp. 3–15.
 A. Scho¨nhage, A. F. W. Grotefeld, and E. Vetter (1994), Fast Algorithms: A Multitape Turing Machine Implementation, B. I.
Wissenschaftsverlag, Mannheim, Germany.
 A. Scho¨nhage and V. Strassen (1971), Schnelle Multiplikation grosser Zahlen, Computing, 7, pp. 281–292.
 P. W. Shor (1994), Algorithms for quantum computation: Discrete logarithms and factoring, in Pro- ceedings of the 35th Annual Symposium on
 (1995), Scheme for reducing decoherence in quantum memory, Phys. Rev. A, 52, pp. 2493–2496.
 D. Simon (1994), On the power of quantum computation, in Proceedings of the 35th Annual Symposium on Foundations of Computer Science,
IEEE Computer Society Press, Los Alamitos, CA, pp. 116– 123.
 T. Sleator and H. Weinfurter (1995), Realizable universal quantum logic gates, Phys. Rev. Lett., 74, pp. 4087–4090.
 R. Solovay (1995), personal communication.
 K. Steiglitz (1988), Two non-standard paradigms for computation: Analog machines and cellular automata, in Performance Limits in
Communication Theory and Practice, Proceedings of the NATO Advanced Study Institute, Il Ciocco, Castelvecchio Pascoli, Tuscany, Italy, July
7–19, 1986, J. K. Skwirzynski, ed., Kluwer Academic Publishers, pp. 173–192.
 W. G. Teich, K. Obermayer, and G. Mahler (1988), Structural basis of multistationary quantum systems II: Effective few-particle dynamics, Phys.
Rev. B, 37, pp. 8111–8121.

REFERENCES
 T. Toffoli (1980), Reversible computing, in Automata, Languages and Programming,
Seventh Collo- quium, Lecture Notes in Computer Science, Vol. 84, J. W. de Bakker and J.
van Leeuwen, eds., Springer, pp. 632–644.
 A. M. Turing (1936), On computable numbers, with an application to the
Entscheidungsproblem, Proc. London Math. Soc. (2), 42, pp. 230–265. Corrections in
Proc. London Math. Soc. (2), 43 (1937), pp. 544–546.
 W. G. Unruh (1995), Maintaining coherence in quantum computers, Phys. Rev. A, 51, pp.
992–997.
 P. van Emde Boas (1990), Machine models and simulations, in Handbook of Theoretical
Computer Science, Vol. A, J. van Leeuwen, ed., Elsevier, Amsterdam, pp. 1–66.
 A. Vergis, K. Steiglitz, and B. Dickinson (1986), The complexity of analog computation,
Math. Comput. Simulation, 28, pp. 91–113.
 A. Yao (1993), Quantum circuit complexity, in Proceedings of the 34th Annual Symposium
on Foun- dations of Computer Science, IEEE Computer Society Press, Los Alamitos, CA,
pp. 352–361.

Automatski - RSA-2048 Cryptography Cracked using Shor's Algorithm on a Quantum Computer

More Related Content

What's hot

Similar to Automatski - RSA-2048 Cryptography Cracked using Shor's Algorithm on a Quantum Computer

Recently uploaded

Automatski - RSA-2048 Cryptography Cracked using Shor's Algorithm on a Quantum Computer