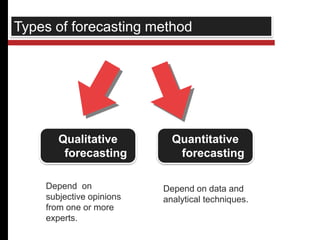
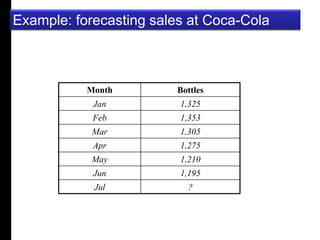
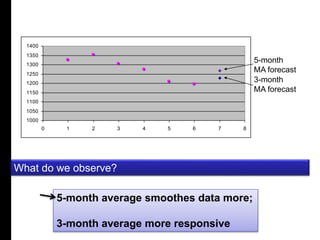
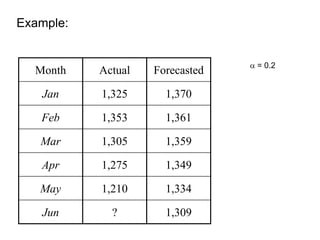
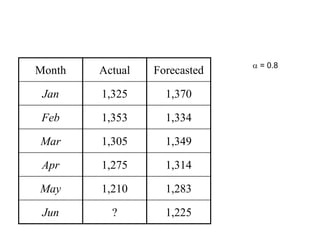
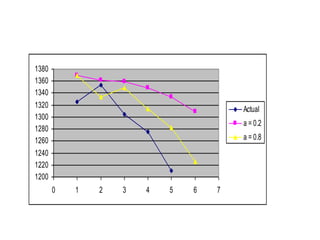
This document discusses quantitative forecasting methods. Quantitative forecasting depends on data and analytical techniques to predict future demand based on past demand information. Some common quantitative forecasting methods discussed include time series analysis, causal models, and simulation. Time series methods like simple moving averages, weighted moving averages, and exponential smoothing are explained as techniques to forecast future demand based on historical data trends. Linear regression models are also mentioned as a way to establish relationships between demand and other factors. Key factors that influence the selection of a forecasting method include data availability, required time horizon, accuracy needs, and available resources.

1. Quantitative Forecasting
Prepared By :-
Jaydeep Kanetiya
Loriya Ravi

2. What is Forecasting ?
 Forecasting is a tool used for predicting future
Forecasting Forecasting is is a a tool tool used used for for predicting
predicting
demand based on past demand information.
future demand based on
past demand information.
future demand based on
past demand information.
Forecasting is a tool used for predicting
 A forecast is only as good as the information
included in the forecast (past data)
future demand based on
past demand information.
 Forecasting is based on the assumption that the past
predicts the future!

3. Types of forecasting method
Qualitative
forecasting
Quantitative
forecasting
Depend on
subjective opinions
from one or more
experts.
Depend on data and
analytical techniques.

4. Quantitative Forecasting
 Time Series: models that predict future
demand based on past history trends
 Causal Relationship: models that use
statistical techniques to establish relationships
between various items and demand
 Simulation: models that can incorporate
some randomness and non-linear effects

5. Time Series : Simple Moving Average method
In the simple moving average models the forecast value is
At + At-1 + … + At-n
Ft+1 = -------------------------------
n
t is the current period.
Ft+1 is the forecast for next period
n is the forecasting horizon (how far back we
look),
A is the actual sales figure from each period.

6. A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
E
R
T
T
Y
D
g
e
Example: forecasting sales at Coca-Cola
Month Bottles
Jan 1,325
Feb 1,353
Mar 1,305
Apr 1,275
May 1,210
Jun 1,195
Jul ?

7. A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
E
R
T
T
Y
D
g
e
What if we use a 3-month simple moving average?
AJun + AMay + AApr
FJul = ----------------------------
3
= 1,227
What if we use a 5-month simple moving average?
AJun + AMay + AApr + AMar + AFeb
FJul = ------------------------------------------
5
= 1,268

8. A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
E
R
T
T
Y
D
g
e
1400
1350
1300
1250
1200
1150
1100
1050
1000
0 1 2 3 4 5 6 7 8
5-month
MA forecast
3-month
MA forecast
What do we observe?
5-month average smoothes data more;
3-month average more responsive

9. Time series : weighted moving average
Ft+1 = wt At + wt-1 At-1 + … + wt-n At-n
wt + wt-1 + … + wt-n = 1
t is the current period.
Ft+1 is the forecast for next period
n is the forecasting horizon (how far back we look),
A is the actual sales figure from each period.
w is the importance (weight) we give to each period

10. A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
E
R
T
T
Y
D
g
e
Why do we need the WMA models?
Month Bottles
Jan 1,325
Feb 1,353
Mar 1,305
Apr 1,275
May 1,210
Jun 1,195
Jul ?
Make the weights for the last
three months more than the
first three months…
6-month
SMA
The higher the importance we
give to recent data, the more
we pick up the declining trend
in our forecast.
WMA
40% / 60%
WMA
30% / 70%
WMA
20% / 80%
July
Forecast
1,277 1,267 1,257 1,247

11. Time series : Exponential Smoothing(ES)
Assume that we are currently in period t. We calculated the
forecast for the last period (Ft-1) and we know the actual
demand last period (At-1) …
( ) 1 1 1    t t t t F F  A F
The smoothing constant α expresses how much our
forecast will react to observed differences…
If α is low: there is little reaction to differences.
If α is high: there is a lot of reaction to differences.

12. Example:
Month Actual Forecasted
Jan 1,325 1,370
Feb 1,353 1,361
Mar 1,305 1,359
Apr 1,275 1,349
May 1,210 1,334
Jun ? 1,309
 = 0.2

13. Month Actual Forecasted
Jan 1,325 1,370
Feb 1,353 1,334
Mar 1,305 1,349
Apr 1,275 1,314
May 1,210 1,283
Jun ? 1,225
 = 0.8

14. 1380
1360
1340
1320
1300
1280
1260
1240
1220
1200
0 1 2 3 4 5 6 7
Actual
a = 0.2
a = 0.8

15. Linear Regression in forecasting
Linear regression is based on
1. Fitting a straight line to data
2. Explaining the change in one variable through changes
in other variables.
dependent variable = a + b  (independent variable)

16. Factor affecting Selection of Method
1. Data availability
2. Time horizon for the forecast
3. Required accuracy
4. Required Resources

17. References
www.csb.uncw.edu
www.prism.gatech.edu
web.calstatela.edu
www.forecasters.org
www.csun.edu