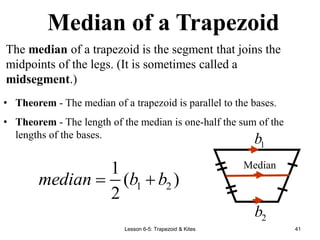
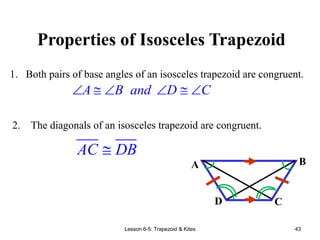
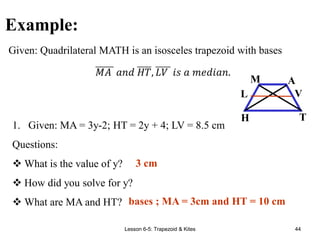
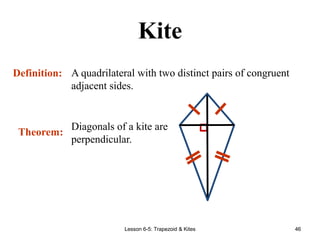
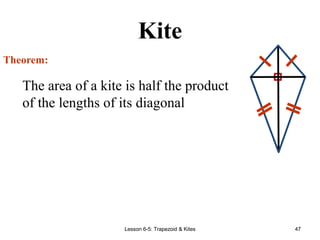
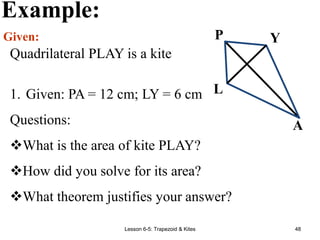
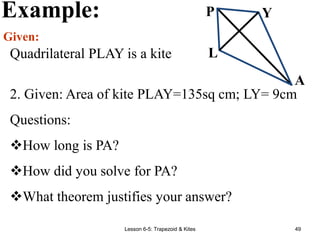
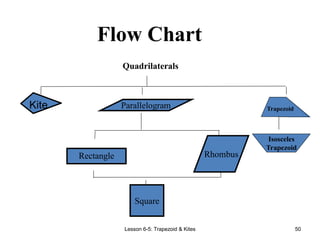
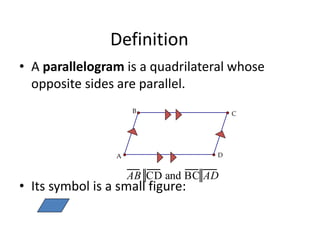
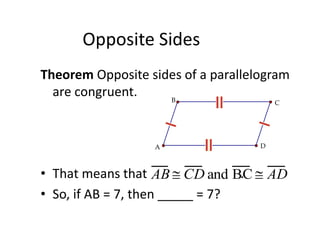
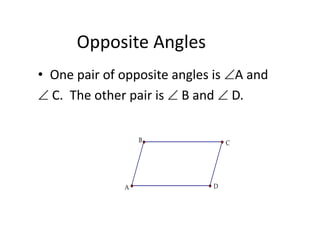
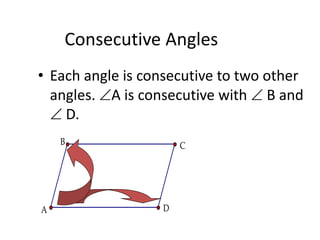
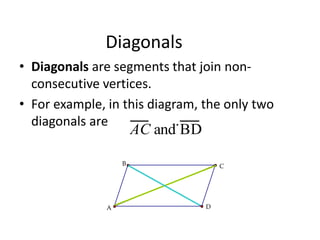
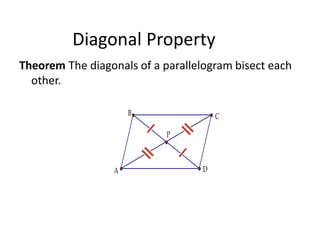
This document provides information about different types of quadrilaterals: [1] It defines parallelograms as quadrilaterals with two pairs of parallel sides, and lists their key properties: opposite sides are parallel and congruent, opposite angles are congruent, and consecutive angles are supplementary. It also discusses the diagonal property. [2] It discusses ways to prove if a quadrilateral is a parallelogram, including if opposite sides are parallel/congruent, opposite angles are congruent, or the diagonals bisect each other. 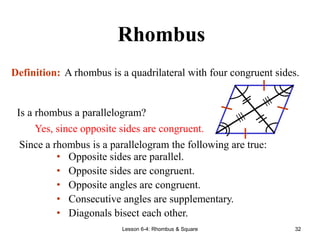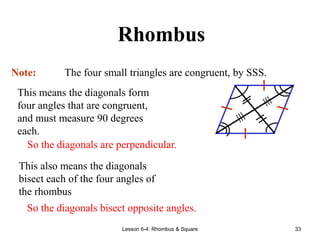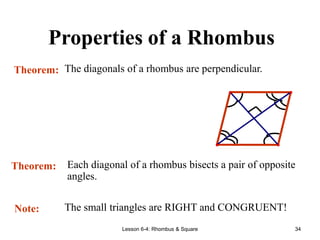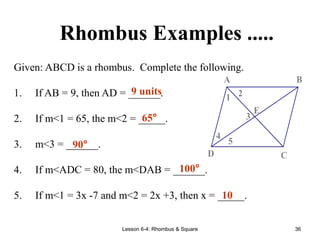[3] It defines rectangles as parallelograms with four right angles, and notes their properties include having congruent diagonals. It also discusses rhomb

2. What parts does the
quadrilateral have?
4 sides
4 vertices
4 angles
2 diagonals

3. Quadrilateral LOVE

4. Quadrilaterals
Part 1
Parallelograms

5. Definition
• A parallelogram is a quadrilateral whose
opposite sides are parallel.
• Its symbol is a small figure:
C
B
A D
AB CD and BC AD

6. Naming a Parallelogram
• A parallelogram is named using all four
vertices.
• You can start from any one vertex, but you
must continue in a clockwise or
counterclockwise direction.
• For example, this can be either
ABCD or ADCB. C
B
A D

7. Basic Properties
• There are four basic properties of all
parallelograms.
• These properties have to do with the angles,
the sides and the diagonals.

8. Opposite Sides
Theorem Opposite sides of a parallelogram
are congruent.
• That means that .
• So, if AB = 7, then _____ = 7?
C
B
A D
AB  CD and BC  AD

9. Opposite Angles
• One pair of opposite angles is A and
 C. The other pair is  B and  D.
C
B
A D

10. Opposite Angles
Theorem Opposite angles of a
parallelogram are congruent.
• Complete: If m  A = 75 and m
 B = 105, then m  C = ______
and m  D = ______ .
C
B
A D

11. Consecutive Angles
• Each angle is consecutive to two other
angles. A is consecutive with  B and
 D.
C
B
A D

12. Consecutive Angles in Parallelograms
Theorem Consecutive angles in a parallelogram are
supplementary.
• Therefore, m  A + m  B = 180 and m
 A + m  D = 180.
• If m<C = 46, then m  B = _____?
C
B
A D
Consecutive
INTERIOR
Angles are
Supplementary!

13. Diagonals
• Diagonals are segments that join non-
consecutive vertices.
• For example, in this diagram, the only two
diagonals are .
AC and BD
C
B
A D

14. Diagonal Property
When the diagonals of a parallelogram intersect, they
meet at the midpoint of each diagonal.
• So, P is the midpoint of .
• Therefore, they bisect each other;
so and .
• But, the diagonals are not congruent!
AC and BD
AP  PC BP PD
P
C
B
A D
AC  BD

15. Diagonal Property
Theorem The diagonals of a parallelogram bisect each
other.
P
C
B
A D

16. Parallelogram Summary
• By its definition, opposite sides are parallel.
Other properties (theorems):
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• The diagonals bisect each other.

17. Examples
• 1. Draw HKLP.
• 2. Complete: HK = _______ and
HP = ________ .
• 3. m<K = m<______ .
• 4. m<L + m<______ = 180.
• 5. If m<P = 65, then m<H = ____,
m<K = ______ and m<L =______ .
LP
KL
P
P
115o
65o
115o

18. Examples (cont’d)
• 6. Draw the diagonals. They intersect at
M.
• 7. Complete: If HM = 5, then ML = ____ .
• 8. If KM = 7, then KP = ____ .
• 9. If HL = 15, then ML = ____ .
• 10. If m<HPK = 36, then m<PKL = ___.
5
7
7.5
36

19. Part 2
Tests for
Parallelograms

20. Review: Properties of
Parallelograms
• Opposite sides are parallel.
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• The diagonals bisect each other.

21. How can you tell if a quadrilateral
is a parallelogram?
• Defn: A quadrilateral is a parallelogram iff
opposite sides are parallel.
• Property If a quadrilateral is a
parallelogram, then opposite sides are
parallel.
• Test If opposite sides of a quadrilateral are
parallel, then it is a parallelogram.

22. Proving Quadrilaterals as Parallelograms
If both pairs of opposite sides of a quadrilateral are
congruent, then the quadrilateral is a parallelogram .
Theorem 1:
H G
E F
If one pair of opposite sides of a quadrilateral are both congruent and
parallel, then the quadrilateral is a parallelogram .
Theorem 2:
If EF GH; FG EH, then Quad. EFGH is a parallelogram.
 
If EF GH and EF || HG, then Quad. EFGH is a parallelogram.


23. Theorem:
If both pairs of opposite angles of a quadrilateral are congruent, then
the quadrilateral is a parallelogram.
Theorem 3:
If the diagonals of a quadrilateral bisect each other, then the
quadrilateral is a parallelogram .
Theorem 4:
H G
E
F
M
,
If H F and E G
     
then Quad. EFGH is a parallelogram.
int
If M is themidpo of EG and FH
then Quad. EFGH is a parallelogram.
EM = GM and HM = FM

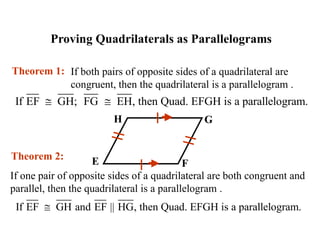
24. 5 ways to prove that a quadrilateral is a parallelogram.
1. Show that both pairs of opposite sides are || . [definition]
2. Show that both pairs of opposite sides are  .
3. Show that one pair of opposite sides are both || and  .
4. Show that both pairs of opposite angles are  .
5. Show that the diagonals bisect each other .

25. Examples ……
Find the values of x and y that ensures the quadrilateral
is a parallelogram.
Example 1:
6x
4x+8
y+2
2y
6x = 4x + 8
2x = 8
x = 4
2y = y + 2
y = 2
Example 2: Find the value of x and y that ensure the quadrilateral is
a parallelogram.
120°
5y°
(2x + 8)°
2x + 8 = 120
2x = 112
x = 56
5y + 120 = 180
5y = 60
y = 12

26. Lesson 6-3: Rectangles 26
Part 3
Rectangles

27. Lesson 6-3: Rectangles 27
Rectangles
• Opposite sides are parallel.
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• Diagonals bisect each other.
Definition:
A rectangle is a quadrilateral with four right
angles.
Is a rectangle a parallelogram?
Thus a rectangle has all the properties of a parallelogram.
Yes, since opposite angles are congruent.

28. Lesson 6-3: Rectangles 28
Properties of Rectangles
Therefore, ∆AEB, ∆BEC, ∆CED, and ∆AED are isosceles
triangles.
If a parallelogram is a rectangle, then its diagonals
are congruent.
E
D C
B
A
Theorem:
Converse: If the diagonals of a parallelogram are
congruent , then the parallelogram is a
rectangle.

29. Lesson 6-3: Rectangles 29
Properties of Rectangles
E
D C
B
A
Parallelogram Properties:
 Opposite sides are parallel.
 Opposite sides are congruent.
 Opposite angles are congruent.
 Consecutive angles are supplementary.
 Diagonals bisect each other.
Plus:
 All angles are right angles.
 Diagonals are congruent.
 Also: ∆AEB, ∆BEC, ∆CED, and ∆AED are
isosceles triangles

30. Lesson 6-3: Rectangles 30
Examples…….
1. If AE = 3x +2 and BE = 29, find the value of x.
2. If AC = 21, then BE = _______.
3. If m<1 = 4x and m<4 = 2x, find the value of x.
4. If m<2 = 40, find m<1, m<3, m<4, m<5 and m<6.
m<1=50,
m<3=40,
m<4=80,
m<5=100,
m<6=40
10.5 units
x = 9 units
x = 18 units
6
5
4
3
2
1
E
D C
B
A

31. Lesson 6-4: Rhombus & Square 31
Part 4
Rhombi
and
Squares

32. Lesson 6-4: Rhombus & Square 32
Rhombus
Definition: A rhombus is a quadrilateral with four congruent sides.
Since a rhombus is a parallelogram the following are true:
• Opposite sides are parallel.
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• Diagonals bisect each other.
Is a rhombus a parallelogram?
Yes, since opposite sides are congruent.

33. Lesson 6-4: Rhombus & Square 33
Rhombus
Note: The four small triangles are congruent, by SSS.
This means the diagonals form
four angles that are congruent,
and must measure 90 degrees
each.
So the diagonals are perpendicular.
This also means the diagonals
bisect each of the four angles of
the rhombus
So the diagonals bisect opposite angles.

34. Lesson 6-4: Rhombus & Square 34
Properties of a Rhombus
Theorem: The diagonals of a rhombus are perpendicular.
Theorem: Each diagonal of a rhombus bisects a pair of opposite
angles.
Note: The small triangles are RIGHT and CONGRUENT!

35. Lesson 6-4: Rhombus & Square 35
Properties of a Rhombus
.
Since a rhombus is a parallelogram the following are true:
• Opposite sides are parallel.
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• Diagonals bisect each other.
Plus:
• All four sides are congruent.
• Diagonals are perpendicular.
• Diagonals bisect opposite angles.
• Also remember: the small triangles are RIGHT and
CONGRUENT!

36. Lesson 6-4: Rhombus & Square 36
Rhombus Examples .....
Given: ABCD is a rhombus. Complete the following.
1. If AB = 9, then AD = ______.
2. If m<1 = 65, the m<2 = _____.
3. m<3 = ______.
4. If m<ADC = 80, the m<DAB = ______.
5. If m<1 = 3x -7 and m<2 = 2x +3, then x = _____.
5
4
3
2
1
E
D C
B
A
9 units
65°
90°
100°
10

37. 37
Square
• Opposite sides are parallel.
• Opposite sides are congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• Diagonals bisect each other.
Plus:
• Four right angles.
• Four congruent sides.
• Diagonals are congruent.
• Diagonals are perpendicular.
• Diagonals bisect opposite angles.
Definition:A square is a quadrilateral with four congruent
angles and four congruent sides.
Since every square is a parallelogram as well as a rhombus and
rectangle, it has all the properties of these quadrilaterals.

38. Lesson 6-4: Rhombus & Square 38
Squares – Examples…...
Given: ABCD is a square. Complete the following.
1. If AB = 10, then AD = _____ and DC = _____.
2. If CE = 5, then DE = _____.
3. m<ABC = _____.
4. m<ACD = _____.
5. m<AED = _____.
8 7 6
5
4
3
2
1
E
D C
B
A
10 units 10 units
5 units
90°
45°
90°

39. Lesson 6-5: Trapezoid & Kites 39
Part 5
Trapezoids
and Kites

40. Lesson 6-5: Trapezoid & Kites 40
Trapezoid
A quadrilateral with exactly one pair of parallel
sides.
Definition:
Base
Leg Trapezoid
The parallel sides are called bases and the non-parallel
sides are called legs.
Leg
Base

41. Lesson 6-5: Trapezoid & Kites 41
The median of a trapezoid is the segment that joins the
midpoints of the legs. (It is sometimes called a
midsegment.)
• Theorem - The median of a trapezoid is parallel to the bases.
• Theorem - The length of the median is one-half the sum of the
lengths of the bases.
Median
1
b
2
b
1 2
1
( )
2
median b b
 
Median of a Trapezoid

42. Lesson 6-5: Trapezoid & Kites 42
Isosceles Trapezoid
A trapezoid with congruent legs.
Definition:
Isosceles
trapezoid

43. Lesson 6-5: Trapezoid & Kites 43
Properties of Isosceles Trapezoid
A B and D C
     
2. The diagonals of an isosceles trapezoid are congruent.
1. Both pairs of base angles of an isosceles trapezoid are congruent.
A B
C
D

AC DB

44. Lesson 6-5: Trapezoid & Kites 44
Example:
1. Given: MA = 3y-2; HT = 2y + 4; LV = 8.5 cm
Questions:
 What is the value of y?
 How did you solve for y?
 What are MA and HT?
Given: Quadrilateral MATH is an isosceles trapezoid with bases
A
M
T
H
V
L
3 cm
bases ; MA = 3cm and HT = 10 cm

45. Lesson 6-5: Trapezoid & Kites 45
Example:
Given: Quadrilateral MATH is an isosceles trapezoid with bases
A
M
T
H
V
L
115

46. Lesson 6-5: Trapezoid & Kites 46
Kite
A quadrilateral with two distinct pairs of congruent
adjacent sides.
Definition:
Theorem:
Diagonals of a kite are
perpendicular.

47. Lesson 6-5: Trapezoid & Kites 47
Kite
Theorem:
The area of a kite is half the product
of the lengths of its diagonal

48. Lesson 6-5: Trapezoid & Kites 48
Example:
Given:
Quadrilateral PLAY is a kite
P Y
L
A
1. Given: PA = 12 cm; LY = 6 cm
Questions:
What is the area of kite PLAY?
How did you solve for its area?
What theorem justifies your answer?

49. Lesson 6-5: Trapezoid & Kites 49
Example:
Given:
Quadrilateral PLAY is a kite
P Y
L
A
2. Given: Area of kite PLAY=135sq cm; LY= 9cm
Questions:
How long is PA?
How did you solve for PA?
What theorem justifies your answer?

50. Lesson 6-5: Trapezoid & Kites 50
Isosceles
Trapezoid
Quadrilaterals
Rectangle
Parallelogram
Rhombus
Square
Flow Chart
Trapezoid
Kite