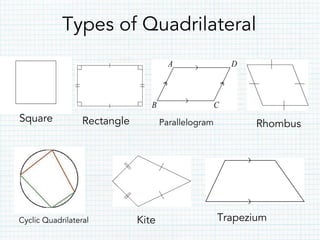
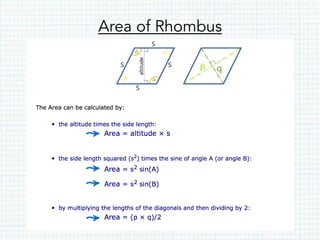
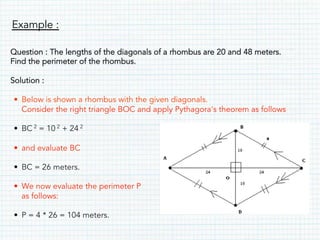
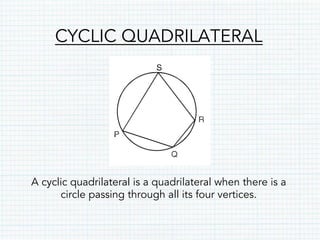
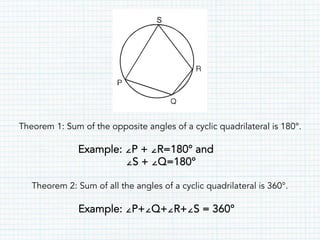
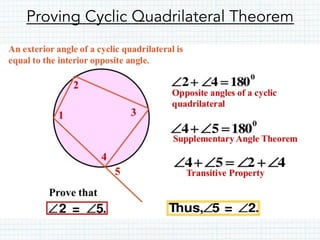
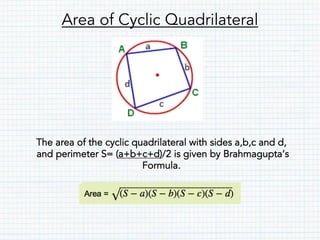
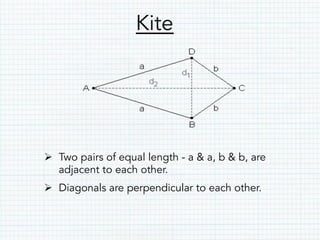
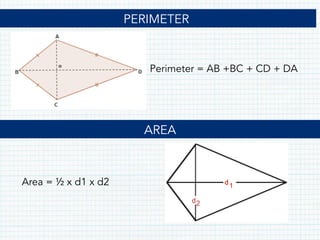
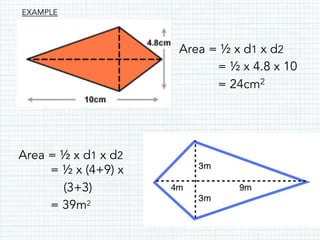
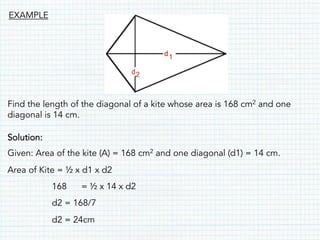
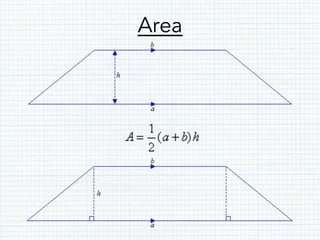
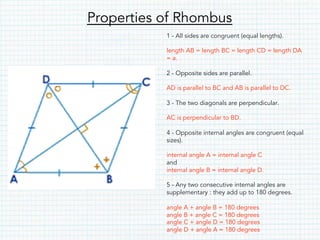
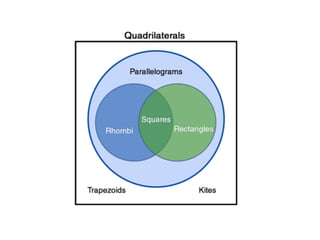
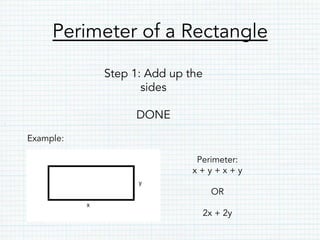
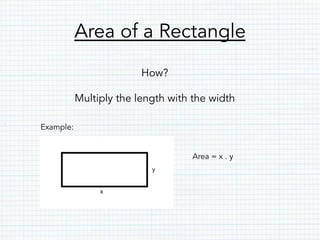
This document defines and provides properties of various quadrilaterals: - A quadrilateral is a four-sided polygon with four interior angles summing to 360 degrees. Types include squares, rectangles, parallelograms, rhombuses, kites, and trapezoids. - Rectangles have opposite parallel sides of equal length and right angles. The perimeter of a rectangle is the sum of its sides, and its area is length multiplied by width. 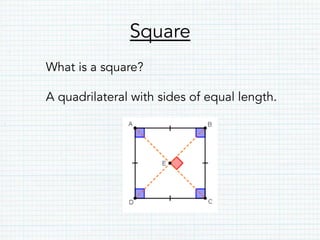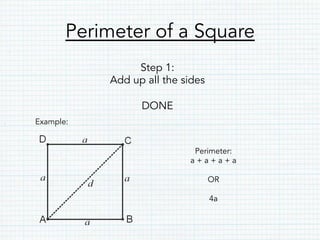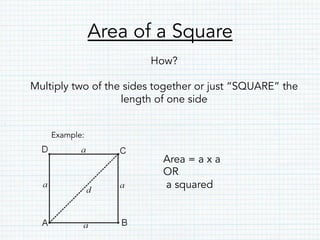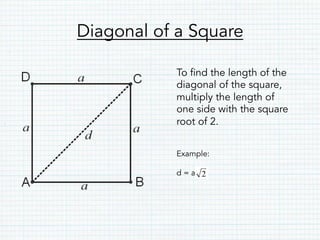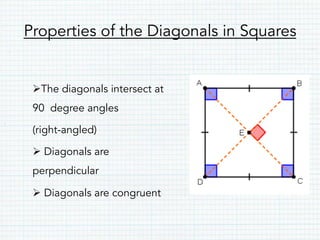- Squares are rectangles with all sides of equal length. The perimeter and area formulas are the same but use only one side length. 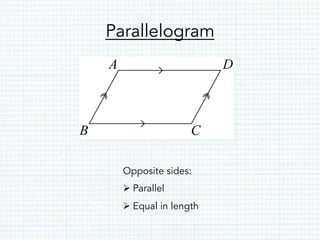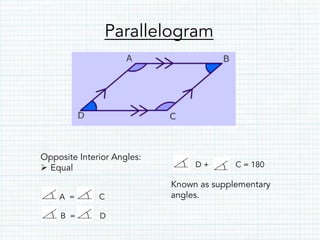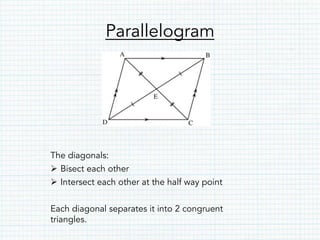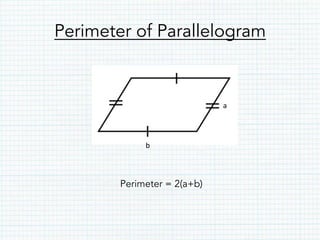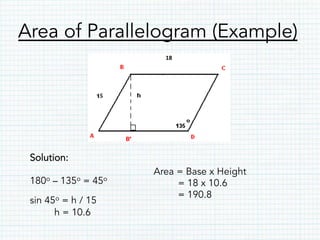- Parallelograms have opposite parallel sides of equal length and opposite interior angles that sum to 180 degrees. The

1. Quadrilateral

2. What is a Quadrilateral ？
Ø It is a four-sided polygon with four angles
Ø The sum of interior angles is 360

3. Types of Quadrilateral
Square Rectangle Parallelogram Rhombus
Kite TrapeziumCyclic Quadrilateral

4. Rectangles and Squares

5. Rectangle
What is a rectangle?
A quadrilateral where opposite sides are parallel.

6. Properties of a Rectangle
Ø Opposite sides are congruent
Ø Opposite sides are parallel
Ø Internal angles are congruent
Ø All internal angles are right angled (90 degrees)

7. Perimeter of a Rectangle
Step 1: Add up the
sides
DONE
Example:
Perimeter:
x + y + x + y
OR
2x + 2y

8. Area of a Rectangle
How?
Multiply the length with the width
Example:
Area = x . y

9. The Diagonal of a Rectangle
To find the length of diagonal on a rectangle:
Let diagonal = D
D squared = x squared + y squared
D

10. Properties of the Diagonals on
Rectangles
Ø Diagonals do not intersect at right angles
Ø Angles at the intersection can differ
Ø Opposite angles at intersection are
congruent

11. Square
What is a square?
A quadrilateral with sides of equal length.

12. Properties of a Square
Ø The sides are congruent
Ø Angles are congruent
Ø Total internal angle is 360 degrees
Ø All internal angles are right-angled
(90 degrees)
Ø Opposite angles are congruent
Ø Opposite sides are congruent
Ø Opposite sides are parallel

13. Perimeter of a Square
Step 1:
Add up all the sides
DONE
Example:
Perimeter:
a + a + a + a
OR
4a

14. Area of a Square
How?
Multiply two of the sides together or just “SQUARE” the
length of one side
Example:
Area = a x a
OR
a squared

15. Diagonal of a Square
To find the length of the
diagonal of the square,
multiply the length of
one side with the square
root of 2.
Example:
d = a

16. Properties of the Diagonals in Squares
Ø The diagonals intersect at
90 degree angles
(right-angled)
Ø Diagonals are
perpendicular
Ø Diagonals are congruent

17. Parallelogram
Opposite sides:
Ø Parallel
Ø Equal in length

18. Parallelogram
Opposite Interior Angles:
Ø Equal
Ø A = C
B = D
D + C = 180
Known as supplementary
angles.

19. Parallelogram
The diagonals:
Ø Bisect each other
Ø Intersect each other at the half way point
Each diagonal separates it into 2 congruent
triangles.

20. Perimeter of Parallelogram
Perimeter = 2(a+b)
a
b

21. Area of Parallelogram
Area = Base x Height

22. Area of Parallelogram (Example)
Solution:
180o – 135o = 45o
sin 45o = h / 15
h = 10.6
18
Area = Base x Height
= 18 x 10.6
= 190.8

23. Rhombus
A flat shape with 4 equal straight sides that looks
like a diamond.

24. Properties of Rhombus
1 - All sides are congruent (equal lengths).
length AB = length BC = length CD = length DA
= a.
2 - Opposite sides are parallel.
AD is parallel to BC and AB is parallel to DC.
3 - The two diagonals are perpendicular.
AC is perpendicular to BD.
4 - Opposite internal angles are congruent (equal
sizes).
internal angle A = internal angle C
and
internal angle B = internal angle D.
5 - Any two consecutive internal angles are
supplementary : they add up to 180 degrees.
angle A + angle B = 180 degrees
angle B + angle C = 180 degrees
angle C + angle D = 180 degrees
angle D + angle A = 180 degrees

25. Area of Rhombus

26. Perimeter of Rhombus

27. Example :
Question : The lengths of the diagonals of a rhombus are 20 and 48 meters.
Find the perimeter of the rhombus.
Solution :
• Below is shown a rhombus with the given diagonals.
Consider the right triangle BOC and apply Pythagora's theorem as follows
• BC 2 = 10 2 + 24 2
• and evaluate BC
• BC = 26 meters.
• We now evaluate the perimeter P
as follows:
• P = 4 * 26 = 104 meters.

28. CYCLIC QUADRILATERAL
A cyclic quadrilateral is a quadrilateral when there is a
circle passing through all its four vertices.

29. Theorem 1: Sum of the opposite angles of a cyclic quadrilateral is 180°.
Example: ∠P + ∠R=180° and
∠S + ∠Q=180°
Theorem 2: Sum of all the angles of a cyclic quadrilateral is 360°.
Example: ∠P+∠Q+∠R+∠S = 360°

30. Proving Cyclic Quadrilateral Theorem

31. Area of Cyclic Quadrilateral
The area of the cyclic quadrilateral with sides a,b,c and d,
and perimeter S= (a+b+c+d)/2 is given by Brahmagupta’s
Formula.

32. Kite
Ø Two pairs of equal length - a & a, b & b, are
adjacent to each other.
Ø Diagonals are perpendicular to each other.

33. Perimeter = AB +BC + CD + DA
Area = ½ x d1 x d2
PERIMETER
AREA

34. Area = ½ x d1 x d2
= ½ x 4.8 x 10
= 24cm2
Area = ½ x d1 x d2
= ½ x (4+9) x
(3+3)
= 39m2
EXAMPLE

35. Find the length of the diagonal of a kite whose area is 168 cm2 and one
diagonal is 14 cm.
Solution:
Given: Area of the kite (A) = 168 cm2 and one diagonal (d1) = 14 cm.
Area of Kite = ½ x d1 x d2
168 = ½ x 14 x d2
d2 = 168/7
d2 = 24cm
EXAMPLE

36. Trapezium
Properties:
Only one pair of opposite side is parallel.

37. Area

39. Example

41. Class Activity

42. Question 1
• Only one pair of opposite side is parallel.

43. Question 2
• Opposite sides are parallel.
• All sides are congruent (equal lengths).
• Opposite internal angles are congruent (equal sizes).
• The two diagonals are perpendicular.
• Any two consecutive internal angles are supplementary : they add up to
180 degrees.

44. Question 3
Opposite sides:
• Parallel
• Equal in length
The diagonals:
• Bisect each other
• Intersect each other at the half way point
Each diagonal separates it into 2 congruent triangles

45. Question 4
• Two pairs of equal length - a & a, b & b, are adjacent
to each other.
• Diagonals are perpendicular to each other.

46. End of Presentation
Thank You.