This document describes algorithms for trajectory generation and control of quadcopters. It discusses: 1) Using splines to generate minimum snap trajectories between waypoints specified in SO(3) space. 2) Developing controllers to track the smooth generated trajectories, including linearized small angle control and altitude control. 3) Extending the control to 3D trajectory tracking using position and velocity error feedback to compute commanded accelerations.

1. Trajectory Generation and Control for
Quadcopter

2. Introduction
As quadcopters are increasingly becoming more and more popular, there is an increasing need of
making these vehicles autonomous. In this work we have designed an algorithm for generation of
smooth minimal snap trajectory given waypoints in SO(3). Each waypoint specifies a desired position,
velocity, yaw, pitch and roll angles in SO(3). Such waypoints can be generated by an RRT algorithm and
our algorithm generates smooth minimum snap (4th
derivative of position) trajectories between these
waypoints. We have also developed a controller that allows our vehicle to track these given smooth
trajectories.

3. Modelling and Control
Important equations governing the motion of the quadcopter are:
Euler equation:

4. The quadrotor is modeled as a rigid body of mass [mg] evolving in the 3-D space. The effects linked to
fluid dynamic are all neglected for our model.
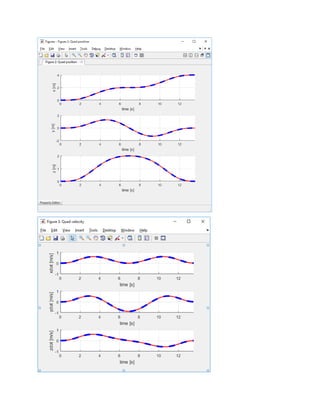
3-D Trajectory Generation
We used a method based on splines that generates a minimum snap trajectory (7th
order polynomial)
between specified waypoints using the Euler-Lagrange equations. Below we explain how to generate the
minimum jerk (5th
order polynomials) trajectory using the method employed.
- We can solve the Euler-Lagrange equation
- to get the condition x(6)
= 0, such that we get the trajectory equation of the form:
- By imposing certain boundary conditions, position, velocity and acceleration constraints, we are
able to extrapolate the coefficients for the above trajectory equation
o Position constraint: x(0) = c0 = a
o Velocity constraints: x ̇(0) = c1 = 0
o Acceleration constraints: x ̈(0) = 2c2 = 0
o Boundary conditions:
Position Acceleration Velocity
t = 0 a 0 0
t = T b 0 0
Similarly, we have to solve for N-1 polynomials
Control Schemes
Small Angle Control
We linearized the equations of motion and motor models (the two equations above in “Modelling and
Control”) in order to find the coefficients of our controller, with a selection of an operating point that
corresponds to nominal hover state,
r = r0, θ = φ = 0, ψ = ψ0, ˙ r = 0, and ˙ φ = ˙ θ = ˙ ψ = 0,
where the roll and pitch angles are small
(cφ ≈ 1, cθ ≈ 1, sφ ≈ φ, and sθ ≈ θ).
At this hover state, the nominal thrusts from the propellers must satisfy the conditions of:
F i,o = mg / 4,
and the motor speeds must satisfy conditions of:

5. ω i,o = ωh = (mg / 4 * kF )^1/2
Altitude Control
Here we discuss the attitude controller to track trajectories in SO(3) that are close to the nominal hover
state where the roll and pitch angles are small. From the Euler equation (equation above in “Modelling
and Control”) if we assume that the products of inertia are small (ideally, they would be 0 because the
axes are close to the principal axis) and
Ixx ≈ Iyy
Because of this symmetry:
We can also assume the component of the angular velocity in the Zb direction (see Quadcopter model
Fig above), r, is small so the rightmost terms in the first two of the above three equations, qr(Izz –
Iyy) and pr(Ixx – Izz) , which are products involving r are small compared to the other terms. We
note that near the nominal hover state ˙ φ ≈ p, ˙ θ ≈ q, and ˙ ψ ≈ r. For these reasons we can use simple
proportional derivative control laws that take the form
The vector of desired rotor speeds can be found from the desired net force (u1,des) and moments (u2,des,
u3,des and u4,des) by inverting

6. .
Position Control
A hover controller is used for station-keeping or maintaining the position at a desired x, y, and z
location.
- Here we use pitch and roll angle to control position in the xW and yW plane
- Here we use u4 to control yaw angle, and u1 to control position along zW
- rT(t), ψT(t) are the trajectory and yaw angle which we are trying to track
- ψT(t) = ψ0 for the hover controller
- The command accelerations, rdes, i, are calculated from PID feedback of the position error,
ei = (ri,T −ri), as
- Then we linearize
to get the relationship between the desired accelerations and roll and pitch angles, which are
given by the following equations:

7. - Invert the above results to compute the values for the roll and pitch angles of the altitude
controller, using the desired acceleration value and the u1,des
3D Trajectory Control
The 3-D Trajectory Controller is used in our project to follow the 3-D trajectories with normal (not too
high or low) acceleration values such as to still maintain the near-hover assumptions. Our approach to
the problem is similar to that described in G. Hoffmann, S. Waslander, and C. Tomlin. Quadrotor
helicopter trajectory tracking control. In AIAA Guidance, Navigation and Control Conference and Exhibit,
Honolulu, Hawaii, April 2008 publication.
The method for calculating the closest point on the trajectory, rT, to the current position, r is as
described below:

8. - Tangent Unit vector of the trajectory associated with that point be ˆt and the desired velocity
vector be ˙ rT.
- We define the position and velocity errors as:
We can ignore position error in the tangent direction by only considering position error in the normal,
ˆn, and bi-normal, ˆb, directions.
- We calculate the commanded acceleration, ¨rdes i, from PD feedback of the position and velocity
errors:
- The ¨ri,T terms in the equation above illustrate the feed forward term on the desired
accelerations, which can be ignored for low accelerations but will significantly bolster the
performance of the controller for high accelerations.
- Finally we use
to compute the desired roll and pitch angles as well as u1,des.

9. Results and Simulation
We tested out control law on several different trajectories as described below:
1) Tracking a Line:

11. 2) Tracking a Helical Ring:

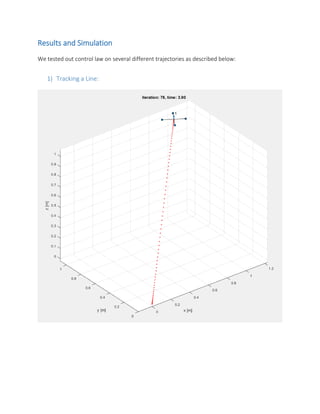
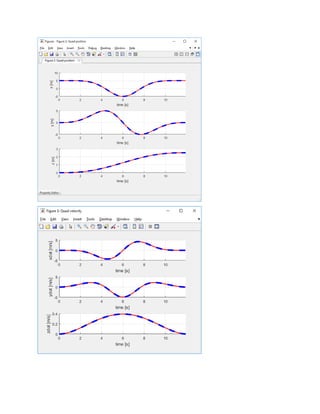
13. 3) Tracking path using given waypoints (Non-smooth trajectory)
waypoints = [0 0 0;
1 1 1;
2 0 2;
3 -1 1;
4 0 0]';

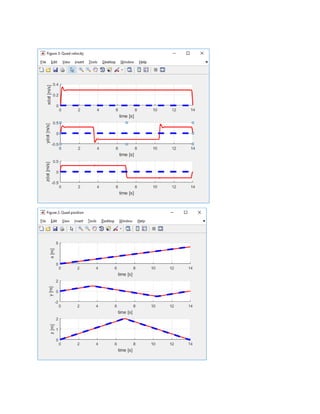
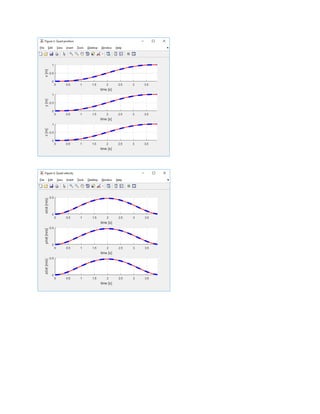
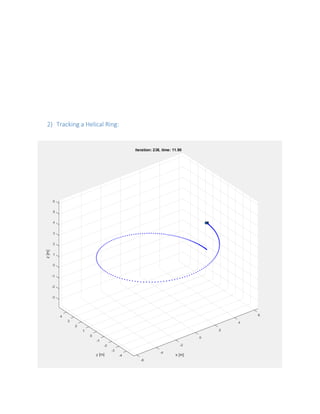
15. 4) Tracking using given waypoints (Using Smooth Minimal Snap Trajectory
Generation)
waypoints = [0 0 0;
1 1 1;
2 0 2;
3 -1 1;
4 0 0]';

17. References
 Mathieu Geisert, Nicolas Mansard. Trajectory Generation for Quadrotor Based Systems using
Numerical Optimal Control. International Conference on Robotics and Automation (ICRA 2016),
May 2016, Stockholm, Sweden. pp. 2958-2964, 2016.
 Mellinger, Daniel Warren, "Trajectory Generation and Control for Quadrotors" (2012).Publicly
Accessible Penn Dissertations.Paper 547.