1. Control of a quadcopter
Pablo Garc´ıa Au˜n´on
M´aster de Intenier´ıa de Sistemas y Control
UNED-UCM
pablogarciaaunon@gmail.com
June 2015
2. Abstract
The aim of this master thesis is to analyzed a complex and multivariable
system, a quadcopter, to model it and develop a controller able to control its
attitude and horizontal and vertical position. The system will be simulated to
check the system response when implementing this controller.
In the first chapter, a state of the art regarding the controller of the quad-
copter is presented. In the second chapter, the dynamic equations of the quad-
copter and the model of the motor’s response are developed. The equations are
then simplified by linearizing them around the equilibrium point. In chapter 3,
only the rotation equations are considered and a controller presented, whereas
in chapter 4 a controller is constructed for the complete model. Since the con-
troller are based on a linearlized model, the system response will be checked for
a linear and a nonlinear model. In chapter 5 a second controller has been also
presented, with a more complex control laws, being able to successfully absorb
external perturbations and changes in the mass of the aircraft. Finally in chap-
ter 6, both controllers are compared with different tests and the conclusions
presented.
3. Chapter 1
Introduction
Quadcopters and their control have being developed in the last 20 years by
many investigation groups all around the world. However, it was only when
the size, consumption and weight of the computers were reduced, when these
aircraft became popular. Nowadays, their use is being regularized gradually in
many countries and it is expected that they will be used in several civil uses in
a near future.
There are presently a wide variety of techniques that may be used to control
them. In [24] a review of a wide set of different controllers, with their advantages
and their drawbacks, is presented. Normally, the quadcopter’s control is divided
in two different levels; one low level controller, in charge of stabilizing the atti-
tude, and a high level one, in charge of controlling the horizontal position. The
vertical movement can be separately controlled.
Linear strategies, and more specifically the well-known PID controllers, may
provide acceptable results if the movement of the quadcopter is slow and close
to the equilibrium point (hovering). For instance, in [16], the attitude of the
quadcopter was stabilized using a PID controller, whereas in [17] the attitude
and the position were controlled by this type of controller. In many cases, the
parameters are tuned intuitively by just observing the system response.
PID controllers can be combined with other methods to improve their per-
formance. In [22] for example, an helicopter was controlled with a PID, which
is switched to different configurations depending on the aircraft’s state. This is
actually an adaptive method, since its configuration changes depending on the
environment and/or the aircraft state. In that case, an adaptive method was
use to improve the robustness of the controller, but also if the system presents
not-well-known characteristics, they might be useful. In [7] for instance, the sys-
tem was supposed to have uncertain mass, inertia and aerodynamic damping
coefficients and the controller was able to deal with these uncertainties.
Another widely used and well-known technique is the backstepping. It con-
sists of dividing the system in different levels and stabilizing them one by one
progressively. In [15], using a quatiernion formulation, a backstepping method
was implemented to stabilize the attitude of the quadcopter, and Lyapunov
functions to prove the stability of the system. To improve the robustness of a
backstepping controller, in [9] an integrator term was added, eliminating steady-
state errors and reducing the response time.
Linear-Quadratic Regulators (LQR) have been also studied. In [2], a PID
1
4. and a LQR controller are compared. The LQR one, which was based on a more
complex model, presents better results. Also feedback linearization [19], robust
control [3] and intelligent techniques [20][8] are used. Even really demanding
controllers in terms of computation cost can now be implemented due to the
improve in the micro-computers in the last years, like predictive control tech-
niques [5]. Despite here only a couple of techniques have been named, one can
get a picture of the diversity of solutions available to control these systems.
In this work, two different backstepping methods are presented and com-
pared. These methods converge fast and need less computational efforts, but
normally their robustness is not specially good. Both controllers separate the
attitude control from the horizontal and vertical position control. In first place,
the attitude is stabilized to lead the quadcopter to the required angles, by
controlling the traction of the propellers. The horizontal position control is sta-
bilized in second place, by assuming that the attitude angles are the variables
that can be controlled. The first and more simple controller is not able to ab-
sorb disturbances, such as horizontal forces or changes in the mass; the second
and more advance one, is capable of handle them. A final comparison will show
these differences.
2
5. Chapter 2
Dynamics of the quadcopter
In this chapter the dynamics of the quadcopter will be analyzed and a model
to represent the behavior of the system will be proposed. Based on the model,
the control’s law will be built up.
2.1 Coordinate frames and transformations
To develop the equations of the quapcopter and its control the next coordinate
frames will be used (see Figure (2.1a)):
• Earth frame (intertial frame): fixed to a point in the earth surface, it is
called ”North-East-Down” system. The zi axes points to the direction
of the center of the earth, xi to the North direction and yi to the East.
Despite the Earth moves, this frame system can be considered as inertial
considering the small displacement and low velocity of the quadcopter.
• Vehicle-carried vertical frame: fix to the center of gravity of the quad-
copter, its axes are parallel to the Earth frame’s ones.
• Body frame: its origin is located at the center of gravity of the quadcopter
and they are fixed to it. Its xbyb plane contains the planes of the rotors
and xbzb is equidistant from all the rotor axes.
To relate the coordinate systems, the Euler angles will be used :
φ: Balance angle
θ: Pitch angle
ψ: Yaw angle
In the Figure (2.1b) those angles have been represented as well as the trans-
formation order from Fv (in blue) to Fb (in red). Note that the order of the
transformations is relevant to transform a vector from one system to the other.
The transformation matrix is therefore:
Rbv =
cθcψ sφsθcψ−cφsψ cφsθcψ+sφsψ
cθsψ sφsθsψ+cφcψ cφsθsψ−sφcψ
−sθ sφcθ cφcθ
(2.1)
3
6. (a) Coordinates frame used (b) Euler angles
Figure 2.1: System response with non-zero initial conditions.
This matrix transforms a vector ub referenced in the body frame system Fb
to vehicle frame system Fv:
uv = Rvb · ub (2.2)
This transformation matrix might be inverted to make the contrary trans-
formation by simply transposing it Rbv = RT
vb.
2.2 Dynamic equations
The quadcopter will be considered as a solid, so that the equations which de-
scribe its dynamics are:
dv(t)
dt i
=
dvb(t)
dt b
+ ωb × vb = g +
Faero
m
+
Fprop
m
(2.3)
dh(t)
dt i
=
dhb(t)
dt b
+ ωb × hb =
Maero
m
+
Mprop
m
(2.4)
where
v velocity of the CoG in Fi
vb velocity of the CoG in Fb
h angular moment in Fi
hb angular moment in Fb
d
dt a
is the derivative in the frame a
ωb is the angular velocity of the quadcopter in Fb
m mass of the quadcopter
g is the acceleration of gravity
4
7. Faero, Maero aerodynamic forces and moments
Fprop, Mprop the propulsive forces and moments (propellers’ traction)
Every term will be determined in the following subsections.
2.2.1 Aerodynamic forces and moments
In a first approximation, they will be considered as negligible, i.e. Faero ≈
Maero ≈ 0. As the quadcopter moves faster, the aerodynamic forces become
higher and make it to move slower. If fact, if we simulated the movement of
the quadcopter without having these forces into account, it would accelerate
indefinitely, which is clearly unrealistic. Anyway, in this work only slow a dis-
placements will be considered and therefore this approximation can be assumed.
2.2.2 Propulsive forces
They are generated by the traction of the 4 propellers installed in the quad-
copter. The forces’ direction is always −zb, are always positive and it will be
assumed that they do not depend on the relative velocity of the air respect each
propeller1
. Therefore, the transfer function of the traction of each propeller, ui,
will be assumed to be:
ui = µ
ωm
s + ωm
vmi
(2.5)
where µ is a constant given, ωm is a bandwidth and vmi
is the voltage
delivered to the engines. In the Figure (2.2) the traction of each propeller and
the direction of rotation have been represented. The total force, resulting from
adding the traction of each propeller, is then T = u1 + u2 + u3 + u4. Normally
a change of variable is used so that the problem is simplified:
u1 + u2 + u3 + u4 = uz (2.6)
2.2.3 Propulsive moments
The moments caused by the traction of the propellers are:
Mx = L = d(u4 − u2) (2.7a)
My = M = d(u1 − u3) (2.7b)
Nz = N = dN (u1 + u3 − u2 − u4) (2.7c)
where d is the distance from the center of the propeller to the CoG in the xbyb
plane and dN is a fictitious distance which represents the aerodynamic reaction
of the propellers due to the draft of the blades. Note that the rotation inertia
of the blades and the motors have been neglected, which will cause moments
1The behavior of the propeller depends highly on it, see [14]. However, such a relative
velocity might be assumed to be much lower than the relative velocity of the air due to the
spin of the blades.
5
8. Figure 2.2: Forces of the propellers and their directions of spin.
.
around the zb axes. As well as in (2.6), the next change of variables is convenient
to be used:
uφ = u4 − u2 (2.8a)
uθ = u1 − u3 (2.8b)
uψ = u1 + u3 − u2 − u4 (2.8c)
On the other hand, the angular moment shall be calculated as:
hb = Ib · ωb (2.9)
where
Ib =
Ix 0 0
0 Iy 0
0 0 Iz
ωb =
p
q
r
Recall that the planes xbyb, xbzb and ybzb are planes of symmetry and there-
fore the non-diagonal elements of the inertia matrix are null.
2.2.4 Equations of the navigation
These equation relate the rotation and the velocity of the quadcopter in the
body frame Fb and its movement in the inertial frame Fi, i.e. the its relative
velocity respect the earth and the Eurler angles:
vv = Rbv · vb (2.11)
˙φ
˙θ
˙ψ
=
1 sφtanθ cφtanθ
0 cφ −sφ
0 sφ/cθ cφ/cθ
ωb (2.12)
6
9. The Equation (2.11) is simply the transformation of the velocity of the quad-
copter in the body frame to the earth frame using Equation (2.1). The Equation
(2.12) is calculated taking into account the order in the transformation in the
Eurler angles.
2.3 Movement equations
Gathering the equations described above one gets finally:
˙u + wq − vr
˙v + ur − wp
˙w + vp − uq
=
−gsθ
gcθsφ
gcθcφ − uz/m
(2.13)
Ix ˙p + (Iz − Iy)rq
Iy ˙q + (Ix − Iz)pr
Iz ˙r + (Iy − Ix)qp
=
d · uφ
d · uθ
dN · uψ
(2.14)
The force equations (2.13) and the moment equations (2.14) together with
(2.12) can be integrated to work out the movement of the quadcopter, given the
propulsion of the propellers. Once it is calculated, the displacement in the earth
frame can be calculated with (2.11). In the Appendix (A.1) the parameters of
the quadcopter have been collected. The state of the system will be defined
then:
x =
u
v
w
p
q
r
φ
θ
ψ
(2.15)
7
12. Chapter 3
3dof controller
3.1 Description of the 3dof system
As a first step, before designing a complete controller for the quadcopter, a
design of the 3dof quadcopter is proposed. This system is made up with 4
propellers and its structure can rotate around its center of gravity, but its dis-
placement is restricted. It will be supposed that the system is equipped by
gyroscopes, able to measure the velocity of rotation in every body axes:
y =
p
q
r
(3.1)
Giving three reference values φr, θr and ψr the system must follow them
actuating its 4 motors.
3.2 Simplification of the equations
The Equation (2.18) calculated in the previous chapter considers 6 degrees of
freedom. For the system studied in this chapter, that equation shall be simplified
eliminating the force equations:
˙˜p
˙˜q
˙˜r
˙˜φ
˙˜θ
˙˜ψ
=
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
˜p
˜q
˜r
˜φ
˜θ
˜ψ
+
0 d
Ix
0 0
0 0 d
Iy
0
0 0 0 dN
Iz
0 0 0 0
0 0 0 0
0 0 0 0
uz
uφ
uθ
uψ
(3.2)
Note that the control uz has no influence on the state of the system so that
it can be chosen freely.
10
13. 3.3 Design of the linear controller
Since the linealized equations are decoupled, each controller can be design sep-
arately. Taking as example the control of φ, from Equation (3.2) one has:
˙˜p = d
Ix
uφ
˙˜φ = ˜p
→
¨˜φ =
d
Ix
uφ (3.3)
To control the variable φ, a PID controller is be proposed. With the Laplace
transform of the previous equation we get:
s2 Ix
d
˜Φ(s) = Uφ(s) (3.4)
If we suppose now that when Uφ is commanded, the commands for the
engines 4 and 2 are equal and but with different sign, Uφ = U4 − U2 = 2U4,
from Equations (2.5) and (2.8) we obtain:
s2 Ix
d
˜Φ = Uφ = 2 · U4 =
2µωm
s + ωm
Vm4
=
2µωm
s + ωm
Vφ (3.5)
and therefore the forward-path transfer function is:
˜Φ
Vφ
= Gp(s) =
2µωmd
Ix
1
s2(s + ωm)
= kφ
1
s2(s + ωm)
(3.6)
The PID controller has the following transfer function Gc(s):
Gc = kP +
kI
s
+ kD · s (3.7)
Having a unity feedback gain, the transfer function of the close-loop system
turns out to be:
Hφ(s) =
Gc · Gp
1 + Gc · Gp
= kφ
kDs2
+ kP s + kI
s4 + s3ωm + kφ(kDs2 + kP s + kI)
(3.8)
In a similar way, we can get the transfer function of the system for the ψ
angle:
Hψ(s) = kψ
kDs2
+ kP s + kI
s4 + s3ωm + kψ(kDs2 + kP s + kI)
(3.9a)
kψ =
4µωmdN
Iz
(3.9b)
Having a look at the previous equations, we can realize that analytically
would not be easy to choose the coefficient of the PID controller, even simplifying
the equation considering kI 1. Therefore, the parameters will be determined
with the help of the PID Tune toolbox within Simulink to reach a suitable
behavior; although this tool does not represent exactly the behavior of the
complete system, it helps as a first step to select the parameters of the controller.
Since there have not been specified any performance requirement, it will be tried
that the system response is as fast as possible with an overshoot lower than 5%,
11
14. Parameter PID - φ, θ PID - ψ
kP 0.0055 1
kI 0.0007 0
kD 0.9 4.9
N 35 100
BM (rad/s) 5.37 2.74
Mr 1.03 1.09
ωr (rad/s) 1.57 0.47
Table 3.1: Values of the parameters of the 3 dof PID controller and their main
characteristics extracted from the Bode diagram.
taking into account the saturation of the motors. For the angle ψ, since the
velocity response is not critical, the overshooting will be set to zero, and the
system response will not be required to be as fast as possible, ensuring then
that the effort needed from the motors is lower.
In the Table (3.1) the parameters of the controller have been written. Notice
that there is a parameter, N, which normally is not used. It is the Filter
Coefficient, which is the pole of the derivative term (an ideal derivative term
would have N = ∞). The transfer function of the controller is then:
FP ID(s) = kP +
kI
s
+ kD
N · s
s + N
(3.10)
This coefficient fillers the signal before deriving it, so that higher frequencies
than N are absorbed. The higher N is, the wider the considered bandwidth of
the signal is.
The some aspects of the performance of the system might be obtained with
the frequency-domain analysis, as well a some conclusions about the sensitivity
and robustness of it. In Figure 3.1 the Bode diagram of the system response, see
Equations 3.8 and 3.9, with the PID controller of Table 3.1 has been represented.
From it, the Bandwidth (BM), the Resonant Peak (Mr) and the Resonant Fre-
quency (ωr) can be obtained; in Table 3.1 all these values have been presented.
Note that the bandwidth of the yaw control is lower than the pitch one, which
means that for reference signals whose frequencies are higher than this value,
the system will have difficulties to follow them. This result is actually consis-
tent, since the dynamics of the system is slower rotating around the zb axes.
Anyway, as it was already pointed out, the yaw requirements are not expected
to be very demanding and therefore this result is acceptable.
Once the inputs uφ, uθ and uψ have been calculated, they must be trans-
formed to the inputs of each motor. Notice that there is a variable not yet
determined, uz, since the movement in the zb direction is impeded. Therefore,
to determine the 4 inputs, this last variable must be chosen. If it were simply
taken as 0, when one the other variables were determined, it would lead to a
negative thrust in at least one engine. The easiest solution might be simply as-
sign a positive value to uz, e.g. the weight, high enough to avoid that situation;
this would be the trimming of the system if it were a quadcopter able to move
in the vertical direction, which is not the case. In the case here studied, a 3dof
quadcotper, this choice would not be the optimal, since the output could be
12
15. Magnitude(dB)
-60
-40
-20
0
20
φ, θ
ψ
10-2
10-1
100
101
102
Phase(deg)
-180
-135
-90
-45
0
45
Bode Diagram
Frequency (rad/s)
Figure 3.1: Bode diagram of the system with the PID controller of Table 3.1.
.
unnecessary restricted because of the saturation of the motors. Knowing that,
an algorithm which calculates a suitable uz has been implemented inside a func-
tion, being known that for low revolutions of the engine the dynamic described
in (2.5) would be slower. Rewriting Equations (2.6) and (2.8) we get:
uθ + uφ + uψ = 2(u4 − u3) (3.11)
The next inequalities must be therefore satisfied:
uθ + uφ + uψ ≤ 2umax (3.12a)
uθ + uφ + uψ ≥ −2umax (3.12b)
If not, the variable uψ will be accordingly restricted so that the previous
condition is fulfilled. Note that if this variable, which has been considered the
less critical and therefore the one to be restricted, were zero, the preliminary
restriction uφ ≤ umax and uθ ≤ umax would be enough to ensure that the
engines are not either saturated or actuated under negative voltages. With this
logic law, the input uz can be freely chosen if uψ is not restricted, or determined
if it is restricted.
In this very function, the actual thrust of each engine, umi
, is calculated as
well, as per (2.6) and (2.8), and afterwards transformed in their corresponding
voltage, Vmi = umi /µ.
As before described, the output from the sensors are the rotational velocity
in every axes, i.e. p, q, r. Since the controller needs the Euler angles, an observer
is needed, which in a first approximation can be taken as a simply integrator
considering Equation (2.18). If the system has a angle measurement unit, this
integrator can be then not used and the angle directly taken from it.
Finally, a maximum rotation rate of 40◦
/s in each axes should be limited for
safety reasons. Although an explicit way of limiting this maximum speed will
not be implemented, it will be checked that this limit is respected, tuning the
gains if they are overtaken.
13
16. time (s)
0 5 10 15 20
angle(deg)
-5
0
5
10
15
20
φ
θ
ψ
(a) Euler angles
time (s)
0 0.5 1 1.5 2
Vm
(V)
-5
0
5
10
15
20
25
V1
V2
V3
V4
(b) Inputs
Figure 3.2: System response with non-zero initial conditions
3.4 Results of the 3dof controller
Once the controller has been configured, it has been tested firstly with the linear
system. The controller must be capable of, giving a initial condition, to make
the system return to the x0 position. Also, it must be able to follow successfully
a reference signal. In a second step, the system will be tested with a non-linear
system using 6dof Euler Angles block, included in the Aerospace Blockset. Since
this provides a movement in every direction and the system here studied has
its movement restricted, the acceleration will be fed back to the forces input of
the block to eliminate those accelerations. In that simulation, it will be shown
that the observer does not provide values accurate enough and a new one will
be proposed.
3.4.1 Linear system
In the Figure (3.2) the response of the system with non-zero initial conditions
has been represented, being φ0 = θ0 = ψ0 = 0.3 rad= 17.2◦
. Note that the pitch
and roll dynamics are considerably faster. The main time-domain characteristics
of the pitch and roll response are the following:
maxover = 7%
td = 0.33 s
tr = 0.44 s
ts = 0.62 s
The dynamics of the roll and the pitch are the same, as it was expected. The
overshoot is higher than the maximum before established; however, this value
is also acceptable. In the case of the yaw angle, it has been preferred to lead
the system so that there is not overshooting, needing 9.5 s to reach the 95% of
the final value. In the Figure (3.2b) the inputs in volts have been represented,
being the maximum and the minimum 22 and 0 V respectively.
Once the controller has been tested with non-zero conditions, a referenced
to be followed has been used. The references are two sinusoidal signals to be
followed by φ and θ while ψ will be kept equal to 0, being the initial conditions
14
17. time (s)
0 5 10 15 20
angle(deg)
-15
-10
-5
0
5
10
15
φ
θ
ψ
(a) ωφ = ωθ = 0.5 rad/s
time (s)
0 0.2 0.4 0.6 0.8 1
angle(deg)
-15
-10
-5
0
5
10
15
φ
θ
ψ
(b) ωφ = ωθ = 10 rad/s
Figure 3.3: System response with zero initial conditions and sinusoidal reference
signal with an amplitude of 0.2 rad, 11.5◦
.
equal to zero. In the Figure (3.3) the input of the system has been represented
as well as the reference signals (dashed lines) for two different frequencies, 0.5
and 10 rad/s. For the lower frequency, see Figure 3.3a, the attenuation is barely
visible, around +0.035 dB, and a phase delay of 8.9◦
, 0.31 s. From the Bode
diagram we would have expected an attenuation of +0.025 dB and a phase delay
of 7.5◦
, which matches pretty well. This results shows that the controller is able
to follow successfully the reference signal. If the frequency increases up to 10
rad/s, the situation is completely different, as can be seen in Figure 3.3b. The
attenuation is clearly visible as well as the phase delay. From the graphic we
identify an attenuation of -13.8 dB and a phase delay of 158◦
, whereas with
the Bode diagram we would expect -11.9 dB and 135◦
. Note also that the first
cycles of the system response do not represent the steady state and therefore
the attenuation and the phase delay have been identified after some oscillations.
The results obtained directly from the system response are not exactly the
same as the ones obtained from the Bode diagram, although both are similar.
The differences might be due the derivative block of the PID controller, in which
the coefficient N is not infinity, what has been assumed in Equation 3.7.
3.4.2 Non-linear system
The controller has been designed assuming the system as linear. Although for
small angles it is a good approximation, if it is not the case, the result may be
really different. On the other hand, the rotation in every axes is coupled, as can
be seen in (2.14), so that when the rotations in the different axes are managed
at the same time, the behavior is non-linear.
In the Figure (3.4a) the response of the non-linear system has been shown,
with the same controller and observer previously used. It must be said, that the
angles here shown are the estimated by the linear observer, which it is nothing
but an integration of the linear Equations (3.2) to obtain the euler angles. The
result seems to be pretty the same as the one obtained using the linearized
system, Figure (3.3b). However, if one observes the real angles, assumed to be
the ones calculated by the 6dof Euler Angles block, one realizes that the yaw
angle is not kept in 0◦
as requested, but oscillates periodically with an amplitude
15
18. time (s)
0 5 10 15 20
angle(deg)
-15
-10
-5
0
5
10
15
φ
θ
ψ
(a) Measurements from the linear observer
time (s)
0 5 10 15 20
angle(deg)
-15
-10
-5
0
5
10
15
φ
θ
ψ
(b) Real values
Figure 3.4: Non-linear system response with zero initial conditions and sinu-
soidal reference signals with ωφ = ωθ = 0.2 rad/s
time (s)
0 5 10 15 20 25 30 35 40
angle(deg)
-15
-10
-5
0
5
10
15
φ
θ
ψ
Figure 3.5: Non-linear system response with zero initial conditions and sinu-
soidal reference signals with ωφ = ωθ = 0.2 rad/s and non-linear observer
.
1.2◦
and a mean value of -0.6◦
. This is due to the fact that a linear observer
has been used to calculate a movement which is not linear in reality. Beside the
oscillation of ψ, apparently, there is no change in the response of the system,
which means that with this frequency the system still behaves as linear.
To improve the yaw response, an improved observer has been used afterwards
which integrates (2.12) to calculate a more accurate value of the attitude of the
quadcopter. In the Figure (3.5) the response of the non-linear system, using the
new non-linear observer has been represented. The system keeps on oscillating in
the yaw axes but now the mean value has been moved to 0◦
and the amplitude
reduced to only 0.2◦
, being this result considerably better. The oscillation
around 0◦
still exists because the controller is not fast enough to cancel it.
16
19. Chapter 4
6dof linear controller
4.1 Description of system
Once the controller for the 3dof quadcopter has been developed, a new con-
troller for the complete 6dof quadcopter is wanted, using the first stabilization
controller for the attitude, angles φ, θ and ψ. The design firstly must be ex-
tended to control the movement in the zb direction so that the quadcopter is
capable of being stabilized in both horizontal axes and in the vertical direction
independently. Finally, a higher level controller will be implemented in order to
allow the quadcopter to move from one point to another, being the coordinates
of those points given in the inertial coordinate frame.
The physical properties of the quadcopter are presented in the Appendix
(A.2). The behavior of the quadcopter will be probably more agile, since Ix, Iy,
Iz and m decrease, and the product µ · Vmax increases. On the other hand, ωm
increases as well, which means that the dynamic of the engines is faster than
the one of the 3dof quadcopter.
4.2 Architecture of the controller
In the Figure (4.1) the architecture of the 6dof controller has been represented
with its different components. First, we have the Quadcopter, which represents
the quadcopter itself and provides the measurements of the gyroscopes and ac-
celerometer to the Observer. This, using that information, processes it and
calculates the state of the quadcopter, i.e. global position and attitude, deliv-
ering it to both controller levels. The High Level Controller, having as input
the estimated position and the Desired position and orientation, calculates the
needed attitude angles and the altitude in the zi direction (which is approxi-
mately zb) to reach the destination point. Finally, the Lower Level Controller
provides the required voltages (Vm) to the engines of the quadcopter so that the
vales φ, θ, ψ and zd are reached adequately. Every component of the system
will be described in detail.
17
20. Quadcopter
Observer
High Level
Controller
Low Level
Controller
𝑦
𝑥
𝜙 𝑑, 𝜃 𝑑, 𝜓 𝑑, 𝑧 𝑑 𝑉𝑚
𝑥
Desired position
and orientation
𝑋, 𝑌, 𝑍, 𝜓 𝑑
Figure 4.1: Architecture of the 6dof controller
.
4.2.1 Quadcopter
The model used to represent the quadcopter is, as used for the design of the
3dof controller, the 6dof Euler Angles block integrated in Simulink, but now the
displacement will be allowed and the weight will be included as external force
in the direction of zi. The model of the dynamic of the engines, Equation (2.5),
will be also included. The output will be the acceleration and the velocity of
rotation in every axes of the body frame Fb.
4.2.2 Observer
The observer here developed is an extension of the non-linear observer used in
the 3dof controller. Given the velocity of rotation in every body axex, wb, it is
integrated using Equation (2.12) and the attitude is then calculated. With it,
the acceleration vector can be transformed from the body frame to the inertial
frame using the matrix of the Equation (2.1), and finally integrated twice to
calculate the global position.
Notice that this observer has two important problems. First, the attitude
angles are an integration of the velocity of rotation, which means that along
the time, errors are integrated as well and this leads to an increase, linearly
dependent on time, of the errors in the measurements of those angles. In the
case of the the global position, it is calculated by integrating the acceleration
twice, so the errors may become bigger even faster. Despite this fact, the first
problem is more critical, since it affects directly to the safety of the aircraft.
Finally, as it will be said afterwards, the High Level Controller needs an
estimation of the total thrust of the propellers, i.e. uz, which will be provided
by the observer as well knowing the voltage provided to the motors, Vmi
.
18
21. Parameter PID - φ, θ PID - ψ PID - z
KP 0.0015 1 5
KI 0 0 0
KD 0.4 2.2 5
N 50 150 50
BM (rad/s) 7.33 9.18 -
Mr 1.00 1.07 -
ωr (rad/s) 0.004 1.40 -
Table 4.1: Values of the parameters of the 6dof PID controller
4.2.3 Low Level Controller
The Low Level Controller is in charge of stabilizing the attitude of the quad-
copter given the desired Euler angles, and of controlling the movement in the
direction zb. The same structure will be used as for the 3dof quadcopter, but
the function which used to control the saturation of the motors will no be used
anymore, since the the variable uz is also given, and the voltage output to the
motors will be restricted to its limits. On the other hand, since the parameters
of the quadcopter have changed, see Appendix (A.2), the PID controllers must
be tuned again to get a good response of the system.
In the Table (4.1) the parameters of the 6dof controller has been shown, with
the new PID controller for the zb direction. The coefficients are now lower, since
the dynamic of the quadcopter is faster (lower mass and inertia and higher thrust
of the motors), while the pole of the derivative term, N, has been increased.
Equations (3.8) and (3.9) are still valid for this controller, but with the
parameters updated. Following a similar procedure, one can obtain the equation
in the Laplace plane that describes the movement in the z axes:
Z(s) = kz
(kDs2
+ kP s + kI)Zr(s) +
g
s
s4 + s3ωm + kz(kDs2 + kP s + kI)
(4.1a)
kz =
4µωm
m
(4.1b)
Since it is not possible to explicitly separate the transfer function, the bode
diagram cannot be directly drawn. Instead of it, the robustness of the controller
will be tested in Section 6.2 by applying a vertical force on the quadcopter and
changing its mass.
In Figure 4.2 the Bode diagram of the θ/φ and ψ controllers has been rep-
resented. As they have been designed, the frequency response is very similar.
Also, in Table 4.1 the bandwidth, the peak and the peak frequency have been
presented. Note that the bandwidth is now higher, meaning that the system
response is faster than the 3dof one.
The configuration of the PID controllers has been tested for changes in the
yaw and pitch angles up to 0.3 rad, 17◦
, keeping in mind that the maximum
spin rate in every axes is 40◦
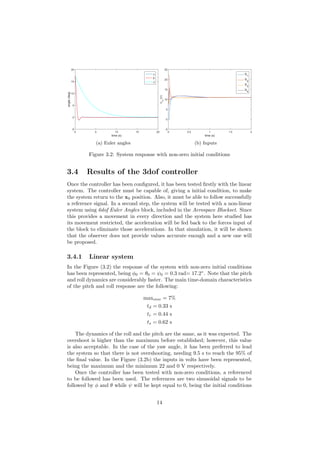
/s. In the Figure (4.3) the response of the system
has been represented, with step reference signals of 1 m for z, 0.3 rad (17.2◦
) for
the pitch and roll angles and 1 rad (57.3◦
) for the yaw angle. z is the altitude in
19
22. Magnitude(dB)
-80
-60
-40
-20
0
20
φ, θ
ψ
10-1
100
101
102
103
Phase(deg)
-180
-135
-90
-45
0
Bode Diagram
Frequency (rad/s)
Figure 4.2: Bode diagram of the system with the PID controller of Table 4.1.
.
Characteristic PID - φ, θ PID - ψ PID - z
maxover (%) 0 0.4 0
td(s) 0.31 1.49 0.41
tr 0.63 2.34 1.00
ts 0.90 4.53 1.55
Table 4.2: Time characteristics of the three controllers, obtained from the results
of Figure 4.3.
the inertial coordinate frame, Fi, since the observer transforms the accelerations
from the body frame to that one. Note that when the aircraft tilts, it looses
altitude slightly because the controller does not compensate directly the lack of
thrust in the zi component, but only when the PID controller acts due to the
difference between the altitude and the reference signal.
In Table 4.2 the time characteristics of the three controllers have been pre-
sented, as well as the overshooting. Opposed to the 3dof controller, these have
been designed so that they do not have overshooting; also, we can remark that
the response is now faster, as it was expected.
4.2.4 High Level Controller
This level of the controller is in charge of generating the reference signals for
the attitude and the altitude to be followed by the Low Level Controller, so
that being given a destination point in the inertial coordinate frame and an
orientation, the quadcopter reaches it.
To control the variables ui and vi, which are the velocities in the inertial
frame and are not directly controllable, the backstepping method will be used.
This technique basically assumes as controllable a variable which is not actually,
and once its wanted value is known, the system is controlled to reach that value.
Assuming values of the attitude small, i.e. φ, θ, ψ 1, the system can be
20
24. linearized and from Equation (2.13) one gets:
˙ub = −gθ (4.2a)
˙vb = gθ (4.2b)
˙wb = g − T/m (4.2c)
Knowing also that ub = Rbvuv, finally we have that:
˙ui = −θ
T
m
(4.3a)
˙vi = φ
T
m
(4.3b)
Then to control ˙ui and ˙vi we will assume as controllable the variables θ and
φ, being T an estimation of total thrust of the propellers, commanded by the
altitude control. If those variables are chosen as:
θd = −
m
T
¨Xd + kDx
( ˙Xd − ˙X) + kPx
(Xd − X) (4.4a)
φd =
m
T
¨Yd + kDy
( ˙Yd − ˙Y ) + kPy
(Yd − Y ) (4.4b)
where X and Y are the position in the inertial frame and Xd and Yd are the
desired position in that very frame, Equations (4.3) become:
¨ex + kDx ˙ex + kPx ex = 0 (4.5a)
¨ey + kDy ˙ey + kPy ey = 0 (4.5b)
having called ex = Xd − X and ey = Yd − Y . The constants kDx
, kPx
, kDy
and
kPy must be chosen properly so that the system converge to ex = ey = 0. For
this case, having tested the complete system, the values taken are:
kDx = kDy = 2.2
kPx = kPy = 1
Once the wanted values, θd and φd, are known, the Low Lever Controller
acts to drive the system to them. The values of zd and ψd are simply passed to
it.
It has been assumed that the attitude angles are small and therefore the
system can be linearized, getting Equation (4.3). However, the yaw angle might
not be negligible at all. To solve this assumption, a change of the coordinates
of the destination points must be carried out:
ˆX
ˆY
=
cos ψ − sin ψ
sin ψ cos ψ
X
Y
(4.7)
Given a position in the inertial frame, X and Y , the controller first change
the coordinate system so that ψ = 0, getting ˆX and ˆY . Afterwards, it calcu-
lates θd and φd through the Equations (4.4), delivering them to the Low Level
Controller.
22
25. time [s]
0 20 40 60 80 100 120
-1
-0.5
0
0.5
1 X
Y
Z
(a) Position of the quadcopter in inertial
frame coordinates
Y [m]
1
0.5
0
10.80.6
X [m]
0.40.20-0.2
1.2
0
0.2
0.4
0.6
0.8
1
-Z[m]
(b) Trajectory of the quadcopter
Figure 4.4: Test of the 6dof controller, following a predefined trajectory
4.3 Results of the 6dof controller
In order to test that the controller works properly, the quadcopter will be com-
manded to reach some points in the space with a specific orientation. Firstly, the
quadcopter will ascend to zi = −0.5 m and then trace a 1-meter-side square in
the space with an orientation of ψd = 0. Having completed that, it will change
its orientation to ψd = π/4 and repeat the same movement in the space but
with an altitude of zi = −1. Despite the orientation changes, the quadcopter
must be capable of reaching the points anyway.
The movement of the quadcopter has been represented in Figure 4.4, follow-
ing the trajectory above described. In the Figure 4.4a the position in inertial
frame coordinates are shown; once the quadcopter reaches zi = −0.5 m, it
moves forward and then to the left, coming back to the origin. Afterwards,
it changes again its high to zi = −1 m and its orientation to ψd = π/4 and
repeats the same movement. Note that even with the change in the orientation
the quadcopter reaches the destination points successfully. In the Figure 4.4b
the 3d movement, estimated by the Observer, has been represented, indicating
the orientation with the blue arrows at some points of the trajectory.
Considering a step input of 1 m, see Figure 4.4a, the time characteristics of
the system response in the x and y direction are:
maxover = 0
td = 1.58 s
tr = 3.72 s
ts = 5.51 s
The attitude and the input of the motors haven represented in Figure 4.5a
and 4.5b respectively. The change in the pitch and roll angles needed to reach
the velocities in every direction are actually small (∼5◦
) so that the linealized
system is closed to the real one. On the other hand, once the yaw angle changes,
the distribution of pitch and roll angles change as well to achieve the attitude
to reach the destination points in the second level of the travel (in the plane
zi = −1). As it can be seen in the Figure (4.5b) the inputs remains always
23
26. time [s]
0 20 40 60 80 100 120
angle[°]
-10
0
10
20
30
40
50
φ
θ
ψ
(a) Attitude (Euler angles)
time [s]
0 20 40 60 80 100 120
Vm[V]
0
2
4
6
8
10
12
14
16
18
20
Vm1
Vm2
Vm3
Vm4
(b) Inputs to the motors
Figure 4.5: Attitude and inputs during the movement represented in Figure
(4.4b)
between their limits, 0 and 20 V.
24
27. Chapter 5
Advanced backstepping
controller
A new a more advanced controller will be presented, which is based on the
backstepping technique, but is build up with more complex laws, capable of
absorbing external forces and changes in the mass. This controller is presented
in [9] and the main contribution of this work is how the parameters have been
selected by using a genetic algorithm.
First, we define a new frame coordinate system k, whose center is the center
of gravity of the quadcopter, its x axes correspond to the k2 axes (see Figure
2.1b), y axes is k1 and z is zv. The angular velocity of this new system is
the ωk = [0, 0, − ˙ψ] so that it can be neglected in Equation (2.3), since it can
be expected only low values of yaw velocities. Taking the state of the system
of Equation (2.15) represented in the frame k, the equation of the motion is
˙x = f(X, U), being
f(X, U) =
uz·Ux+Dx
m
uz·Uy+Dy
m
−uz·cos φ cos θ
m + Dz
m + g
Iy−Iz
Ix
rq + d
Ix
· uφ
Iz−Ix
Iy
pr + d
Iy
· uθ
Ix−Iy
Iz
qp + dN
Iz
· uψ
p
q
r
(5.1)
where Di are disturbances, in N, in every axes; ux and uy are the coefficients
to project the traction in both axes:
−ux = cos φ sin θ cos ψ + sin φ sin ψ (5.2a)
−uy = cos φ sin θ sin ψ − sin φ cos ψ (5.2b)
25
28. Three different controllers will be developed: attitude, position and altitude,
based on the backstepping technique. In the three cases, we have a system of
two variables:
˙x1 = x2 (5.3a)
˙x2 = a · u + b (5.3b)
where u is the controllable variable which, as it can be seen, cannot directly
control x1, the variable to be controlled. We define then the error for the
variable to be controlled and for the pseudo control variable x2:
e1 = x1d − x1 (5.4a)
e2 = x2d − x2 (5.4b)
being x1d the desired value of the variable to be controlled. Note that x2d can
be chosen freely. A Lyapunov function is proposed:
V =
1
2
λp2
+
1
2
e2
1 +
1
2
e2
2 (5.5)
having defined ˙p = e1. To ensure the convergence of the system, the function
V must be positive-definite and its derivative negative-definite:
˙V = λp ˙p + e1 ˙e1 + e2 ˙e2 (5.6)
knowing that ˙e1 = ˙x1d − ˙x1 = ˙x1d + e2 − x2d, we finally get:
˙V = λpe1 + e1( ˙x1d − x2d) + e2(˙e2 + e1) (5.7)
choosing
x2d = ˙x1d + c1e1 + λp (5.8a)
˙e2 = −e1 − c2e2 (5.8b)
the derivative of the Lyapunov function turns out to be:
˙V = −c1e2
1 − c2e2
2 (5.9)
which is definite-negative and ensures the convergence. Deriving Equations
(5.8a) and (5.8b) and with Equation (5.3b), we finally get the control law:
u =
(1 − c2
1 + λ)e1 + (c1 + c2)e2 − c1λp + ¨x1d − b
a
(5.10)
The integer term of the controller will be implemented as adaptive, so that
when the error is lower than a certain limit, p is non zero:
p =
0 if e1 ≥ e1λlim
p if e1 < eλlim
(5.11)
This will reduce the overshooting of the system.
26
29. 5.1 Attitude control
To control the three attitude variables θ, φ and ψ, Equation (5.10) shall be used,
being from Equation (5.1):
bφ =
Iy − Iz
Ix
rq aφ =
d
Ix
(5.12a)
bθ =
Iz − Ix
Iy
pr aθ =
d
Iy
(5.12b)
bψ =
Ix − Iy
Iz
qp aθ =
dN
Iz
(5.12c)
5.2 Position control
The position controller differs from the one developed for the attitude control
because of the consideration of a perturbation force Di in both axes. However,
a similar procedure will be followed. These perturbations will be estimated and
included in the control law:
˜Di = Di − ˆDi (5.13)
where ˆDi is the estimated value of the perturbation, D is the actual perturbation
value and ˜Di is the error made. These perturbations will be considered as
constant, or better said, its dynamics are much slower than the ones involved
in the estimation of the perturbation:
˙˜Di −
˙ˆDi (5.14)
Having said that, let’s assume that there exists, for the control along the x
axes, the next Lyapunov function:
V = V (px, e1x, e2x, ˜D) (5.15)
whose derivative would be:
˙V = ˙px
∂V
∂px
+ ˙e1x
∂V
∂e1x
+ ˙e2x
∂V
∂e2x
+ ˙˜Dx
∂V
∂ ˜Dx
(5.16)
Considering Equations (5.3a), (5.4b), (5.8a) and (5.4b), the error ex2 can be
calculated as:
˙e2x = c1xe1x + ¨x1d + λxpx − ¨x1 (5.17)
and with Equation (5.14) we get:
˙V = ˙px
∂V
∂px
+ λx
∂V
∂e2x
+ ˙e1x
∂V
∂e1x
+ c1x
∂V
∂e2x
+
+ ¨xd −
uxu1 + Dx
m
∂V
∂e2x
−
˙ˆDx
∂V
∂ ˜Dx
(5.18)
ux shall be chosen so that the function ˙V is definite negative. Making u1
m ux =
ux1 + ux2 and ux1 = ¨xd − ˆDx, the previous equation is simplified to:
˙V = ˙px
∂V
∂px
+ λx
∂V
∂ex2
+ ˙ex1
∂V
∂ex1
+ cx1
∂V
∂ex2
− ux2
∂V
∂ex2
−
ˆDx − Dx
m
∂V
∂ex2
−
˙ˆDx
∂V
∂ ˜Dx
(5.19)
27
30. Now, lets divide again the term ux2 into two, ux2 = ux3 + ux4, and taking
ux3 = ˙pxλx + ˙e1xc1x, we get:
˙V = ˙px
∂V
∂px
+ ˙e1x
∂V
∂e1x
− ux4
∂V
∂e2x
−
˜Dx
m
∂V
∂e2x
−
˙ˆDx
∂V
∂ ˜Dx
(5.20)
The last term can be chosen as:
ux4 =
˙px
∂V
∂px
+ ˙e1x
∂V
∂e1x
∂V
∂e2x
+ kx
∂V
∂e2x
and as result, the derivative is:
˙V = −kx
∂V
∂ex2
2
−
˜Dx
m
∂V
∂ex2
−
˙ˆDx
∂V
∂ ˜Dx
(5.21)
We still have to choose the law of the estimated perturbation and the depen-
dency of the function V on ˜D. If we take:
˙ˆDx = −γx
∂V
∂ex2
(5.22)
∂V
∂ ˜Dx
=
˜Dx
mγx
(5.23)
both terms cancel each other, having finally:
˙V = −kx
∂V
∂ex2
2
(5.24)
which is definite-negative, being the convergence ensured. To define the control
terms u1 and u4 and the perturbation law ˆD, the partial derivative ∂V
∂ex2
must
be chosen:
∂V
∂ex2
= βx1px + βx2ex1 + βx3ex2 (5.25)
The Lyapunov function is then, considering also Equation (5.23)
V = β1xpxe2x + β2xe1xe2x + β3xe2
2x +
˜D2
x
2mγx
+ (·) (5.26)
Note that the last term of the function has not been specified, since it is
not needed to determine the control and the perturbation law. However, to
ensure the convergence of the system, with the explicit construction of the Lya-
punov functions, it must be shown that V is definite-positive. Here, a Implicit
Lyapunov Function (ILF, see [1]) has been used so that it is not necessary to
explicitly specified it1
. The control law is then:
ux =
m
u1
¨xd − ˆDx + ˙pxλx + ˙e1xc1x +
β1x ˙px + β2x ˙e1x ˙e2x
β1xpx + β2xe1x + β3xe2x
kx(β1xpx + β2xe1x + β3xe2x) (5.27)
1In the paper where this controller is developed [9] is not explicitly proved the convergence
of the system, since a function g(V, X) must have been specified.
28
31. ˆDx =
t
0
˙ˆDxdτ = −γx
t
0
(β1xpx + β2xe1x + β3xe2x) dτ (5.28)
The same control law can be applied for the y axes. Once ux and uy have
been determined, the desired angles φ and θ can be then calculated from Equa-
tion (5.2):
cos φd sin θd
sin φd
= −
cos ψ sin ψ
sin ψ − cos ψ
ux
uy
(5.29)
From the second equation φd can be obtained and afterwards θd from the
first one. Both values will be then passed to the attitude control.
5.3 Altitude control
In the altitude control not only a perturbation force will be considered, see
Equation (5.13), but also a variation in the mass:
˜m = m − ˆm (5.30)
where ˆm is the estimation of the mass and ˜m is the error in that estimation.
A change in the mass of the quadcopter will seldom happen and will be only
due a change in its payload or because during a mission it is needed to drop a
load. However, an automatic system which allows to automatically detect those
changes might be interesting, since the software does not need to be reconfigured
by hand every time the mass changes, or even to develop a flexible controller
that adapts to different aircraft.
The next Lyapunov function is proposed:
V =
1
2
λzp2
z +
1
2
e2
1z +
1
2
e2
2z +
˜m2
2mγ1z
+
˜D2
z
2mγ2z
(5.31)
which is definite-positive. Its derivative is:
˙V = λzpz ˙pz + e1z ˙e1z + e2z ˙e2z −
˜m ˙ˆm
mγ1z
−
˜D
˙ˆD
mγ2z
(5.32)
Equation (5.10) can be used, being:
a = −
αz
m
; ˆa = −
αz
ˆm
b =
Dz
m
+ g; ˆb =
ˆDz
ˆm
+ g
being αz = cos φ cos θ and all the variables with (ˆ·) are estimated variables. The
control law will be then, using the estimated variables ˆa and ˆb:
u =
(1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨z1d −
ˆD
ˆm + g
−αz
ˆm
(5.34)
29
32. We have also from Equation (5.3b) the movement in the z direction, and
considering the real values a and b:
˙z2 = a · u + b
=
ˆm
m
(1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨z1d − g
+
˜Dz
m
+ g (5.35)
Lets choose ˙z2d equal to the next expression:
˙z2d =
m
m
(1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨z1d − g
+g − c2ze2z − e1z (5.36)
The error ˙e2z turns out to be:
˙e2z = ˙x2d − ˙x2 = −c2ze2z − e1z
+
˜m
m
(1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨zd − g −
˜Dz
m
(5.37)
With this last result, the derivative becomes:
˙V = −c1ze2
1z − c2ze2
2z
+
˜m
m
e2z (1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨zd − g −
˙ˆm
γ1z
−
˜D
m
e2z +
˙ˆD
γ2z
(5.38)
And to make it definite-negative, the law to control the mass estimation and
the vertical perturbation will be taken as:
˙ˆm = γ1ze2z (1 − c2
1z + λz)e1z + (c1z + c2z)e2z − c1zλzpz + ¨zd − g (5.39)
˙ˆDz = −γ2ze2z (5.40)
and therefore the derivative becomes ˙V = −c1ze2
1z − c2ze2
2z. Integrating Equa-
tions (5.39) and (5.40) the estimation of the mass and the perturbation can be
obtained. We then have finally the following control law:
u1 = −
ˆm
αz
(1 − c2
1z
+ λz)e1z
+ (c1z
+ c2z
)e2z
− c1z
λzp + ¨z1d − g +
ˆD
αz
(5.41a)
ˆm =
t
0
˙ˆmdτ (5.41b)
ˆDz =
t
0
˙ˆDzdτ (5.41c)
30
33. 5.4 Parameter selection
5.4.1 Use of genetic algorithms
One of the goals pursued when designing a controller is that it is easy to tune,
and one of the characteristics of the easy-to-tune controllers is normally that
they have a reduced number of parameters. Having a look on the controller just
presented, one can realized that it is not the case at all. Note that the controller
presented in Section 4 only has 6 parameters in the low level controller and 2
more for the high level one.
For the attitude control, we have a total of 3 parameters for every axes,
and 1 more if we consider the limit to start using the integral term of the con-
trol. Considering that the controller for θ and φ will have the same parameters
because of symmetry reasons, there are 8 parameters to be chosen:
c1θ,φ
c2θ,φ
λθ,φ eθ,φ
λlim
(5.42a)
c1ψ
c2ψ
λψ eψ
λlim
(5.42b)
The situation in the position controller is even worst. For the x and y
position control, we have a total number of 8 parameters, having taken into
consideration that for both axis the controller has the same configuration and
that the perturbation ˆD has its own law:
c1x,y
λx,y ex,y
λlim
kx,y γx,y β1x,y β2x,y β3x,y (5.43)
In the case of altitude control, we have 4 parameters, and 2 more for the
perturbation and the mass estimation:
λz ez
λlim
γ1z γ2z c1z c2z (5.44)
In total, the controller requires on 22 parameters to be specified. Note that
he control laws are quite complicated and it would be very tricky to analytically
draw conclusions about how the parameters influence the response of the system,
even if the model is simplified by a linearization, for example. Knowing that,
non-so-conventional approaches must be consider.
The use of intelligent system, and more particularly the evolutionary algo-
rithms (EA), have been used in the control theory in the last 30 years, see[11].
The EA enclose a set of techniques in which one can underline evolutionary pro-
gramming, evolution strategies, genetic programming and genetic algorithms.
Genetic algorithms (GA) are methods for robust search and optimization
based on natural selection principles and population genetics. Basically they
try to look for a sub-optimal solution of a problem when the number of possible
parameters or solutions make impossible scan them properly because computa-
tional costs. GA were popularized by Goldberg in 1989 and are the most used
method for control purposes, followed by genetic programming. Its two main
uses in the control theory are off-line design and the on-line optimization, being
the first one way more used since the the difficulties using the on-line design
associated with using them in real time.
In the search of a sub-optimal solution, a evaluation or fitting function must
be proposed so that the algorithm objectively verifies how good a solution is.
This function represents then the desired objectives of the solution and it might
31
34. take into account penalties for not wanted behaviors. In case we have more
than one objective to be fulfilled, the problem becomes harder, since only one
scalar value is to be used to distinguish between good and bad solutions. One
can try to integrate both evaluation function into only one, taking into account
the importance of each objective by means of weights, see [12].
GA have been used to optimize the PID parameters of the controllers in
different fields from the 90s (see [21] and [23] for instance), but also in the H-
infinity and LQG control (see [6]), among others. Particularly they have been
implemented to tune the PID controller of a quadcopter in [10] and even as
a methodological method of designing UAVs in [18]. However, in the field in
which GA have been widely implemented for UAVs, is in the path planning,
optimal routing and strategical and tactical planning.
In general, we can find the following elements when using this method:
• Initial population: it is the set of solutions proposed initially. They can
be seeded on the search space randomly, uniformly spaced, heuristically,
with good solutions which are previously known or a combination of them.
Normally in a number between 20 and 100, this number is preserved along
the generations. Also the so called islands can be used, which are groups
of populations which progress in parallel and can interchanged genetic
material in punctual moments.
• Representation: we have to distinguish two different concepts or do-
mains. On one hand, we have the genotype space, which is the represen-
tation of the parameters to be optimized so that the algorithm is able
to manipulate them. In the early beginning, a binary representation was
usually implemented, but real numbers or any other data structure can be
also used. On the other hand, we have the phenotype space, which is the
real space of the parameters in the model, normally real numbers. The
transformation from the phenotype to the genotype is called encoding,
whereas the other way around is called decoding.
• Evaluation: every generation of solutions must be evaluated in order to
know how they are fulfilling an objective. A fitness value, which measures
the performance of each member is normally used and the the complete
generation can be ordered in a ranking. Note that it is necessary to finally
obtain a single scalar value, either absolute of relative to the rest of the
members of the generation.
• Selection: once the current population has been evaluated, the next step
is to select the members which are going to produced the next generation of
solution. The tournament method consist of once group of pairs have been
selected, they compete between them and the genetic material form the
winner will be then used. The roulette wheel is on the contrary a method
in which the parents are chosen randomly with a probability proportional
to the fitness value, i.e. the better the fitness value is, the higher the
probabilities of being chosen as parent is. Beside these two methods,
there exists many other, such as the stochastic universal sampling or the
truncation selection.
• Recombination: or crossover, is how the parents interchange their ge-
netic material and its a crucial feature in the GA. There are multiple ways
32
35. of carrying it out; for instance, complete pieces of genes can be taken ran-
domly from one of the parents, or the complete chain of genes can be
split and interchanged between them. Often the frequency with which the
genetic material is interchanged is reduced when generations go by. The
new members are called offspring.
• Mutation: after the recombination, a mutation might be considered,
which is a random change in one of the genes. It allows to randomly
explore other search spaces, which might have been discarded, and gives a
chance to recover good genetic material. The probability of the mutation
is normally taken as 1/Np, where Np is the number of members in each
generation; this way, a mutation is statistically carried out at least once
in each generation.
• Next generation: with the offspring and the new material possibly mu-
tated, a new generation must be chosen. It might be only the new mem-
bers from the offspring or a combination between them and the previous
generation.
As can be seen, there are several elements involved in GA and a lot of
possibilities to configure it. A wrong configuration of its parameter might lead
to poor solutions.
5.4.2 Attitude controller
For the attitude controller a configuration similar to the one used in [21] will be
used:
Initial population
The initial population will be made up with Np = 30 members, whose parame-
ters are chosen randomly between their limits, which are:
c1θ,φ
∈ [0, 25] c2θ,φ
∈ [0, 10] λθ,φ ∈ [0, 5] eθ,φ
λlim
∈ [0, 0.5]
c1ψ
∈ [0, 20] c2ψ
∈ [0, 10] λψ ∈ [0, 5] eψ
λlim
∈ [0, 0.5]
These limits have been established by simply simulating them until the re-
sponse was not acceptable. Having a look later on at the results, these limits
can be confirmed.
Representation
In this case, we will represent the parameters as real numbers.
Evaluation
The attitude controller takes care of stabilizing the dynamics of the quadcopter
in its three axes independently, i.e. the attitude angles θ, φ and ψ. Since it
is assumed a double symmetry in the xbzb and ybzb planes, the controller for
the θ and φ angles will be the same and therefore, only θ will be tested. Then,
we will arrange two different tests, one for θ and another one for ψ, which
will consist of following a step command with different amplitudes, and with
33
36. time [s]
0 5 10 15 20 25 30 35 40
θ[rad]
-0.05
0
0.05
0.1
0.15
0.2
θ
θc
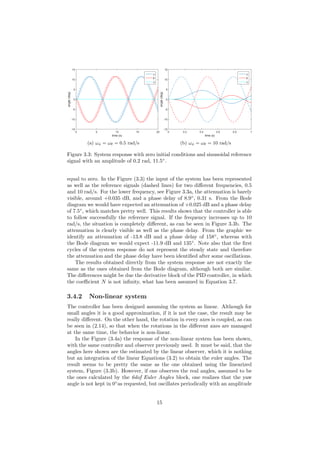
Figure 5.1: Example
two perturbations. In the Figure 5.1 an example of test for θ with a nominal
commanded value of 0.16 rad. The two perturbations are clearly visible at
t = 10 and 30 seconds. The nominal commanded values will be:
θcn
= [
π
4
,
3π
20
,
π
20
, −
π
20
, −
3π
20
, −
π
4
]
ψcn
= [π,
3π
5
,
π
5
, −
π
5
, −
3π
5
, −π]
For every test, three parameters will be measured. First, the quadratic error
of the overall simulation divided by the nominal commanded value, averaged
for the 6 tests:
Eθ =
1
6
6
i=1
(˜eθi + ˜eφi )
Eψ =
1
6
6
i=1
˜eψi
where the subscript i indicates the number of test and the squared errors are
defined as:
˜eθi =
1
θcni
tmax
0
(θ − θci
)
2
dt
˜eφi
=
1
θcni
tmax
0
(φ − φci
)
2
dt
˜eψi
=
1
ψcni
tmax
0
(ψ − ψci
)
2
dt
Secondly, the effort of the controller will be measured as well, being it defied
34
37. as:
σθ =
1
6
6
i=1
tmax
0
u2
θi
+ u2
φi
θcni
dt
σψ =
1
6
6
i=1
tmax
0
u2
ψi
ψcni
dt
being uθi
, uφi
and uψi
the control commands already shown.
Finally, for high values of the parameters, one can realize that the kickback
phenomenon may appear, which is a return in the controlled value before having
reached the desired value. Moreover, with those high values, also high frequency
oscillations might also show up. To penalize these situations, another measure-
ment value will be used, kb, which is the number of zeros in the derivative of
the angle, being they closer than 0.2 seconds one from each other. Also, we will
penalize the overshooting by adding one unit to kb for every 2% of overshooting
if it is higher than 5%; otherwise, no penalty will be applied.
We need to integrate all three measure values in one fitting variable. Lets
define firstly a sub-fitting variable for each performance variable and for each
member m of the population p:
ˆfm
E =
min(Ep
)
Em
ˆfm
σ =
min(σp
)
σm
ˆfm
kb =
min(kb)
kbm
In the above expression, it was not explicitly written either θ nor ψ since
they are valid for both variables. The operator min() is the minimum value of
the population p, so that the performance variables ˆfm
have a maximum value
of 1, which correspond to the member m with the best performance. The higher
a member Em
, σm
of kbm
has, the lower the value ˆf will be. Note that now
every performance parameter has been transformed so that they do not have
unit and their range goes from 0 to 1; we are able now to define a single fitting
variable:
ˆfm
= ˆfm
E + ασ · ˆfm
σ + αkb · ˆfm
kb (5.51)
where ασ and αkb are coefficients to weight the importance of every term. We
can even define better the fitting function by:
fm
=
ˆfm
max( ˆfm)
(5.52)
so that fm
is normalized. The only remaining thing is to choose the values for
the two weights ασ and αkb. Both values have been chosen after some trials,
looking for a good combination between fast response and not so high efforts:
ασθ
= 0.5 αkbθ
= 2
ασψ
= 1 αkbψ
= 2
35
38. Selection
Given a fitting value fm
for every member, the roulette wheel method will be
used to create the matting pool, which will be composed by a number of pairs
equal to the size of the population (Np = 30). These pairs will be chosen
from the previous generation randomly, taking into account a probability which
depends on the fitting value ˆfm
as follows:
Pm
=
fm
Np
i=1
fi
(5.54)
One parent will not be allowed to be matched with itself and the same pair
in the matting pool will be avoid either. It must be pointed out, that there will
be two independent matting pool, one for the θ variable and another one for ψ.
Recombination
For every pair of parents from the matting pool (recall that there are two), and
for every parameter of the solution, one will be taken randomly from one parent
to form the next generation. We will then obtain Np new solutions after the
recombination.
Although this method was the one used in [21], the new material which is
introduced in the generation is very small, since the recombination only takes
the material from one of the parents. One realizes after some simulations that
the complete generation tends to converge to a few different members.
Another recombination is proposed, which consists of making an weighted
average of both parents:
κoff = r · κ1 + (1 − r) · κ2 (5.55)
where κi is the parameter of the parent i and r is a random number between
0 and 1. This new method produces generations with members much more
different between them.
Mutation
For every parameter, there will be a probability of Pmut = 1/Np to be mutated;
this value is often taken so statistically is ensured, that in every generation there
will be at least one mutation in every parameter. If the mutation takes place,
it will happen as follows:
κ = κ + sign(0.5 − r1) ·
κmax
2
· r2 (5.56)
where r1 and r2 are two random number. If κ turns out to be negative, the
previous equation will be again calculated with new random parameters until it
becomes positive.
Next generation
The next generation will be made up with the best Np members of the previous
generation and the offspring generated from them.
36
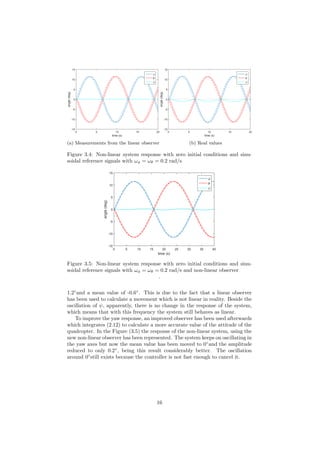
39. Config. c1 c2 λ eλlim
E σ kb f
θ,φ
1 24.1 2.92 2.73 0.10 0.194 9.68 0.167 1
2 6.30 4.43 4.80 0.01 0.210 3.68 0.167 0.985
3 15.9 2.59 0.78 0.06 0.235 4.64 0.167 0.949
4 4.74 4.99 0.31 0.22 0.250 2.25 0.167 0.948
ψ
1 2.92 0.058 0.036 0.087 4.23 9.46 0.167 1
2 3.31 0.058 0.036 0.192 4.38 10.55 0 0.966
3 3.92 0.007 0.267 0.182 4.55 12.9 0.167 0.915
4 3.44 0.176 0.072 0.242 3.67 15.9 0 0.910
Table 5.1: Parameters of the best 4 configurations found by the genetic algo-
rithm, with their quadratic error E, effort σ and kickback measurement kb.
The above configuration will be run a maximum of 50 generations, being
stopped if in 5 generations in a row, there is not an improvement in the best
member of a 5%. Four different simulations will be carried out, two with the
recombination proposed in [21] and two more with the recombination based on
the weighted average of the two parents.
In the Table 3.1 the parameters of the four best configurations found by the
genetic algorithm for the θ/φ and for the ψ controller have been presented. Also
the values of the quadratic error E, the effort σ and the kickback number kb
haven also written, with the relative fitting value f. Note that configuration are
ordered so that the Configuration 1 is the best and the 4 is the worst.
The solutions for the controller of θ and φ are quite different between them,
although the final result is very similar. The configuration 1 has a very high c1
value so the effort is much higher than in the other configurations. Note that
for the four configurations there is at least a kickback in one of the 6 test, being
the kb = 1/6 = 0.167. On the other hand, the parameters for the ψ controller
are more similar between them, although the results are not.
In the Figure 5.2 the time response of both controllers, with their four config-
urations, have been represented for an nominal input of θcn = 0.3 and ψcn = 1
rad. In the case of the pitch angle, see Figure 5.2a, configurations 1 and 2 are
very similar and the only clearly visible difference is that in presence of a pertur-
bation, configuration 1 returns to the reference value faster and therefore, the
error is lower, see Table 5.1. However, configuration 1 needs a way higher effort
and the likelihood of that the kickback shows up is also higher. Therefore, con-
figuration 2 will be chosen. On the other hand, for the angle ψ, Figure 5.2b, it
can be seen that configuration 4 is the best results in terms of velocity response
and error and it has not overshooting; however, it requires much more effort and
since the yaw control is not a relevant nor critical operation, it could prevent
the θ and φ controller to fulfill their duties in the best possible way. Because of
this, configuration 4 has been discarded and configuration 1 has been chosen,
which still has a fast response with a slight overshooting, but it requires less
control effort.
The parameters of the controllers chosen, with their main response charac-
teristics, have been presented in Table 5.2. The percentage of overshooting, the
delay time td, the rise time, tr and the settling time ts, all in seconds, have been
calculated having as a reference response the one shown in Figure 5.2.
37
40. time [s]
0 5 10 15 20 25 30 35 40
θ[rad]
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Pitch angle θcn
=0.3
θc
Conf. 1
Conf. 2
Conf. 3
Conf. 4
(a) Time response of the 4 best
configurations of the θ and φ con-
troller.
time [s]
0 5 10 15 20 25 30 35 40
ψ[rad]
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
Yaw angle ψcn
=1
ψc
Conf. 1
Conf. 2
Conf. 3
Conf. 4
(b) Time response of the 4 best
configurations of the ψ controller.
Figure 5.2: Time response of the controller with the best 4 configurations found,
see Table 5.1.
c1 c2 λ eλlim
maxover (%) td tr ts
θ,φ 6.30 4.43 4.80 0.01 - 0.27 0.42 0.82
ψ 2.92 0.058 0.036 0.087 2.8 1.88 4.03 5.68
Table 5.2: Values of the parameters of the controllers chosen, and their main
response characteristics of Figure 5.2.
38
41. 5.4.3 Position Controller
In the case of the position controller, there are more parameters to be deter-
mined. Also, there are more elements involved in the movement; not only a
position must be reached, but also the perturbation ˆD and the mass ˆm must be
estimated by different tests. As done with the attitude controller, the following
elements of the GA will be taken into consideration.
Initial population
The initial population will be taken randomly between a range of values, deter-
mined after some trials:
c1x,y
∈ [0, 5] λx,y ∈ [0, 2] ex,y
λlim
∈ [0, 0.1] kx,y ∈ [0, 5]
γx,y ∈ [0, 1] β1x,y ∈ [0, 2] β2x,y ∈ [0, 0.5] β3x,y ∈ [0, 5]
λz ∈ [0, 0.5] ez
λlim
∈ [0, 1] γ1z ∈ [0, 0.1]
γ2z ∈ [0, 0.1] c1z ∈ [0, 0.5] c2z ∈ [0, 2]
We will use again Np = 30 members. Since this controller is specially com-
plicated to be tuned, its likely that the first generations are made up with very
bad solutions. Therefore, 5 solutions with good performance will be included in
the initial population.
Representation
Again, the parameters will be represented as real numbers.
Evaluation
The performance of the controller of the x and y direction will be tested by
commanding different positions in the x direction, keeping altitude and position
along y direction. Also, different perturbation forces will be applied to the
quadcopter. The complete sequence of action to test the horizontal position
controller is:
1. Wait 2 second to stabilize the quadcopter in the z direction.
2. Go forward 1 m.
3. Go backward 2 m.
4. Go forward 7 m.
5. Go backward 13 m.
6. Go forward 23 m.
7. Go backward 33 m.
8. Go forward 10 m. back to the initial position.
9. Apply a perturbation force of 1 N.
10. Apply a perturbation force of 2 N.
39
42. 11. Reduce the perturbation force to 0.5 N.
In case of the vertical position controller, the position and a perturbation
will be tested, but also a change in the mass. It must be remarked that a
change in the mass will imply a vertical force in the zb direction and therefore
the controller must interpreter as a perturbation Dz. This means that when
evaluating the ability of the controller to identify a change in the mass, the
perturbation estimation must be disable, and the other way around. Two test
will be carried out
The first test, to evaluate the altitude change and the ability of detecting
vertical perturbations:
1. Disable the detection of the mass change.
2. Wait 2 second to stabilize the quadcopter in the z direction.
3. Ascend 1 m.
4. Ascend 5 m.
5. Ascend 20 m.
6. Descend 20 m.
7. Descend 5 m.
8. Descend 1 m, back to the initial position.
9. Apply a perturbation force of 2 N in the zb direction.
10. Apply a perturbation force of 4 N.
11. Reduce the perturbation force to 1 N.
12. Remove the perturbation.
The second test, to evaluate the ability of detecting changes in the mass of
the quadcotper:
1. Disable the detection of the perturbation.
2. Change the mass of the quadcopter to m0 + 0.150 kg.
3. Change the mass of the quadcopter to m0 + 0.300 kg.
4. Change the mass of the quadcopter to m0 − 0.150 kg.
5. Change the mass of the quadcopter to m0 − 0.300 kg.
It must be pointed out that we might have proposed different experiments
to determined the best parameters solution for the ˆm and ˆD, and afterwards
other experiment to best fit the remaining parameters. However, we would then
choose some parameters taking into account only the ˆm and ˆD estimation, and
then they might not be appropriate for the quadcopter’s movement, since the
controller depends directly on them.
40
43. To evaluate the performance of the controller, as similar approach made for
the attitude controller will be done. On one hand, we will consider the quadratic
error, define as:
Ex =
tmax
0
(x − xc)2
dt +
tmax
0
y2
dt
Ez =
tmax
0
(z − zc)2
dt
On the other hand, the effort will be also considered in the same way it was
done for the attitude controller:
σx =
tmax
0
(u2
x + u2
y)dt
σz =
tmax
0
(u1 − m0 · g)2
dt
where in the vertical effort the weight has been subtracted to better represent
the effort to change the altitude.
Although a slow or bad estimation of the ˆD or ˆm would imply higher er-
rors and efforts, it is convenient to also consider them separately in the final
evaluation function by the following variables:
E ˆDx
=
tmax
0
˜D2
xdt
E ˆDz
=
tmax
0
˜D2
zdt
E ˆm =
tmax
0
˜m2
dt
Since both controllers, especially the zb one, present easily overshoot, another
evaluating variable will be included:
Eover =
0 if maxover ≤ 5%
100 · maxover − 5 if maxover > 5%
(5.61)
Here the maxover accounts the addition of the total overshooting in every step
of the reference signals.
The fitting function will be composed as it was done for the attitude con-
troller:
ˆfm
E =
min(Ep
)
Em
ˆfm
σ =
min(σp
)
σm
ˆfm
E ˆD
=
min(Ep
ˆD
)
Em
ˆD
ˆfm
E ˆm
=
min(Ep
ˆm)
Em
ˆm
ˆfm
over =
1 + min(Ep
over)
max (Em
over, 1)
41
44. where p refers to the complete population and m only the member under study.
All the fitting functions will be included in a single value:
ˆfm
x = ˆfm
Ex
+ ασx
· ˆfm
σx
+ α ˆDx
· ˆfm
E ˆDx
+ αoverx
· ˆfm
overx
ˆfm
z = ˆfm
Ez
+ ασz
· ˆfm
σz
+ α ˆDz
· ˆfm
E ˆDz
+ α ˆm · ˆfm
E ˆm
+ αoverz
· ˆfm
overz
and finally the fitting value of each member can be change so that the maximum
value is 1:
fm
x =
ˆfm
x
max( ˆfm
x )
fm
z =
ˆfm
z
max( ˆfm
z )
The values of the proportional parameters to evaluate the fitting value will
be taken as:
ασx = 0.5 α ˆDx
= 2.5 αoverx = 1.5
ασz = 0.5 α ˆDz
= 1.5 α ˆm = 1.5 αoverz = 2
Selection, recombination and next generation
All three will be carried out same way as it was done for the attitude controller.
Once the evaluation has been established, the algorithm is run for a maxi-
mum of 50 generations, being stopped if the improvement is lower than 5% in
5 generations in a row. Several simulations are carried out, and from each one
the best members are taken and used in the next simulations. It is relatively
easy to find acceptable solutions for the x and y controller, but not for the z
controller, which is more sensitive to the parameters.
In Table 5.3 the best 4 configuration have been taken and their evaluating
values presented. The configurations of the x and y axes are very similar,
since the values of the fitting function f are all close to 1. Having a look at
the response, configuration 3 will be taken, since its able to absorb faster the
perturbations Dx. The case of the altitude controller is different, since there
is a remarkable difference between the best configuration and the second one;
configuration 1 will be selected then.
The values of all parameters will be then:
c1x,y = 0.813 λx,y = 1.53 ex,y
λlim
= 0.152 kx,y = 2.39
γx,y = 0.435 β1x,y = 0.196 β2x,y = 0.140 β3x,y = 1.54
λz = 0.0010 ez
λlim
= 0.143 γ1z
= 0.219
γ2z
= 3.21 c1z
0.819 c2z
= 4.93
In Figure 5.3 the system response, for the planned test, has been represented,
with the configurations selected; the reference signals and the true values are in
blue, and in red the real and estimated values. The first two figures correspond
to the test in the xb direction, whereas the other three correspond to the altitude
controller and the estimation of the mass.
42
45. Config. E σ E ˆD E ˆm Eover f
x,y
1 1488 3.33 56.0 - 0.98 1
2 1535 2.86 59.7 - 0 0.98
3 1498 3.12 67.9 - 0.12 0.94
4 1475 3.29 37.1 - 23.0 0.87
z
1 222 1933 67.6 0.113 0 1
2 211 1796 58.5 0.125 6.21 0.74
3 221 1689 63.4 0.115 27.5 0.69
4 224 1582 60.8 0.155 27.1 0.64
Table 5.3: Parameters of the best 4 configurations found by the genetic algo-
rithm, with their quadratic error E, effort σ and kickback measurement kb.
In Figure 5.3a the movement in the xb direction can be seen; the quadcopter
is able to follow the reference signals successfully with a slight overshooting.
When the reference signal is zero, from t = 70 s on, the movements due to the
perturbations are visible, although the quadcopter comes back to the desired
position rapidly. In Figure 5.3b the perturbation in the xb direction has been
represented, as well as the estimated value. When a reference xb value is com-
manded, the algorithm estimates a perturbation which actually does not exist;
furthermore, when the perturbation actually exists, the algorithm needs long
times to approach the final value, see convergence to the step values. Although
the estimation seems to not work properly, the fact is that the controller absorbs
them properly.
In Figure 5.3c the movement in the zb direction has been represented. As it
happened with the horizontal controller, the reference value is followed without
problem and without overshooting. The perturbations due to Dz are also well
absorbed. This controller is more capable of estimating the perturbation, as
can be seen in Figure 5.3d. Finally, in Figure 5.3e the estimation of the mass
has been shown. The algorithm estimates fast and accurately the real mass of
the quadcopter; it must be pointed out, that in this test, there is no change
of altitude and the perturbation estimation in the zb direction, ˆDz, has been
disabled.
As already indicated, the mass and the vertical perturbation estimation
might be misinterpreted by the algorithm; a change in the mass can be seen
as an addition of a vertical force, and the other way around. Actually, when a
change of altitude is commanded, ˆDz and ˆm become non-zero. Since the mass
is not expected to change during the flight, the mass estimation will be only ac-
tivated during a short time in the beginning of the flight, while the quadcopter
hovers at a certain altitude; once the mass has been calculated, we will force
˙ˆm = 0. Keeping in mind the result of Figure 5.3e, the estimation might need
less than 5 s.
The configuration already defined will be tested with the same trajectory in
Figure 4.4a. Initially, the quadcopter is grounded and the mass is increased in
0.3 kg, so that the controller estimates it after taking off. Also, a perturbation
of 2 N will be afterwards applied in xb and yb axes, at t =45 and 65 s, and of 3
N in the zb direction at t =85 s. In Figure 5.4a, the position of the quadcopter
has been represented, in dotted lines the reference values and solid lines the
43
46. time [s]
0 20 40 60 80 100 120 140 160
X[m]
-10
-8
-6
-4
-2
0
2
4
6
8
10
Xr
X
(a) Movement in the xb direction.
time [s]
0 20 40 60 80 100 120 140 160ˆDx[N]
-3
-2
-1
0
1
2
3
Dx
ˆDx
(b) Estimation of the perturbation
Dx.
time [s]
0 20 40 60 80 100 120 140 160
Z[m]
-26
-24
-22
-20
-18
-16
-14
-12
-10
Zr
Z
(c) Movement in the zb direction.
time [s]
0 20 40 60 80 100 120 140 160
ˆDz[N]
-5
-4
-3
-2
-1
0
1
2
3
4
5
Dz
ˆDz
(d) Estimation of the perturba-
tion Dx.
time [s]
0 5 10 15 20 25 30
ˆm[kg]
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
m
ˆmz
(e) Estimation of the mass m.
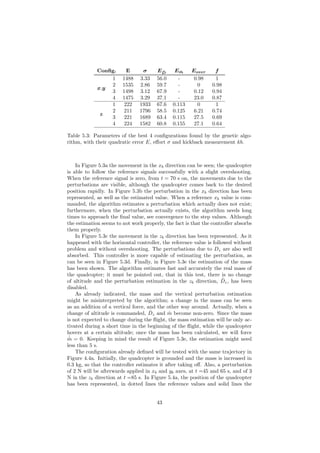
Figure 5.3: Result of the tests with configuration 3 for the controller in the xb
and yb direction and controller 1 in the zb direction.
44
47. Characteristic x, y z
maxover (%) 6 -
td(s) 1.05 0.81
tr 1.52 2.14
ts 3.42 3.28
Table 5.4: Time characteristics of the two nonlinear controllers of the horizontal
and vertical positioning, with reference values x = 1 m and z = −1 m.
actual values. The controller is able to absorb firstly the excess of mass in the
first seconds, and afterwards the disturbances on every axes.
In Figure 5.4b the disturbances on the quadcopter and their estimation have
been represented. The three estimation remain close to the zero value until the
perturbations take place at 45, 65 and 85 s. The estimated values converge
approximately to the real values; although the approximation is not perfect, the
controller absorbs the perturbation, as can be seen in Figure 5.4a.
Finally, in Figure 5.4c the mass estimation and its real value has been shown.
Within 6 seconds, the algorithm estimates perfectly the real mass of the quad-
copter; afterwards, the mass estimation is disable and the final value used from
then on. The take off of the quadcopter delays the convergence of the estimation;
if we had considered that the quadcopter was already hovering, the convergence
would have taken place in less than 2 s. Once the mass has been estimated, its
value it passed to the x and y controller, see Equation 5.2; the update of the
value improves remarkably the performance of the position control, specially
when absorbing external perturbations.
It must be remark that the result here achieve seem to be better than those
obtained in [9]. Of course the quadcopter model is different and the final values
of the parameters are not specified, but the results present overshooting, high
oscillations and irregularities. The method there used to choose the parameters
is not specified.
45
48. time [s]
0 20 40 60 80 100 120
Position[m]
-1.5
-1
-0.5
0
0.5
1
1.5
X
Y
Z
(a) Position of the quadcopter.
time [s]
0 20 40 60 80 100 120
ˆD
-3
-2
-1
0
1
2
3
ˆDx
ˆDx
ˆDx
(b) Estimation of the perturba-
tions.
time [s]
0 1 2 3 4 5 6
ˆm
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
(c) Estimation of the mass m dur-
ing the first 5 seconds.
Figure 5.4: Test with the final configuration of the controller, similar to the one
in Figure 4.4a, but with a change of +0.3 kg in the mass and perturbations in
the three axes.
46
49. Chapter 6
Comparison of both
controllers
Once we have completely defined the nonlinear controller, we can compare it
with the linear one, developed in the beginning of this work.
6.1 Attitude stabilization controller
First, we will compare the low level controller, in charge of stabilizing the quad-
copter’s attitude, i.e. the angles θ, φ and ψ. The time characteristics of both
controllers are:
Controller maxover (%) td(s) tr ts
θ,φ
Linear - 0.31 0.63 0.90
Nonlinear - 0.27 0.42 0.82
ψ
Linear 0.5 1.49 2.34 4.53
Nonlinear 3 1.88 4.03 5.68
The nonlinear controller presents a faster response stabilizing the θ and φ
angles, whereas the response in the ψ angle is faster with the linear controller.
In Figure 6.1, the system response for both controllers have been represented,
being the commanded values θc =0.3 rad and θc =1 rad. the system is perturbed
with a constant moment in the θ and ψ angles at t = 2 and 10 s respectively.
In Figure 6.1a, the theta response has been represented. As expected, the
nonlinear controllers converges faster to the reference signal and also recovers
rapidly from the perturbation. On the other hand, the linear controller is not
capable of absorb the perturbation and remains around 0.87 rad. The controller
is not capable of reducing the error because of the low value of the proportional
coefficient of the PID controller, kP = 0.0015. Although the PID configura-
tion tracks the references well, it does it when there are changes on them and
therefore if the references remain constant and the angle changes because of
47
50. time [s]
0 1 2 3 4 5
θ[rad]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Reference
Lineal
Non-lineal
(a) Pitch angle response.
time [s]
0 5 10 15 20
ψ[rad]
0
0.2
0.4
0.6
0.8
1
1.2
Reference
Lineal
Non-lineal
(b) Yaw angle response.
Figure 6.1: System response comparison between the linear controller, in red,
and the nonlinear controller, in red.
a perturbation, the controller does not succeed on coming back to the desired
value. Furthermore, if we take a look on the needed effort, defined by Equation
5.49, we have:
σθlinear
= 0.40
σθnonlinear
= 0.24
the effort is much higher in the linear controller, so the nonlinear controller is
visibly better.
The case of the ψ controller is different. As said, the PID controller con-
verges faster to the reference signal, but it needs more time to recover after the
perturbation. Also, the efforts are:
σψlinear
= 2.86
σψnonlinear
= 0.70
The effort needed by the linear controller is 40 times higher than the one
needed by the nonlinear controller. If we needed the yaw response to be faster,
we could configure the parameter selection algorithm so that the error is more
important, by reducing the weight of the effort.
6.2 Position controllers
To compare both high level controller, we will design 5 different tests. First,
the system response reaching the positions x = 1 m and z = −1 m will be
analyzed independently. Another two experiments will be carried out, in which
an external force in the x and −z will be applied, while the quadcopter tries to
remain in the initial position. Finally, an additional mass will be added and the
altitude will be checked to see if the controllers are able to keep it. In Figure
6.2 all the tests’ results have been presented.
In Figure 6.2a the system response with both controllers have been shown,
when commanded with a reference signal x =1 m. The nonlinear controller
turns out to be faster, having a small overshooting. On the other hand, in Figure
48
51. 6.2b the movement in the zb axes can be seen, being initially the quadcopter
grounded and taking off to an altitude of z = −1 m. In this case, the linear
controller is faster than the nonlinear one. The time domain characteristics of
both controllers, in both axes are the following:
Controller maxover (%) td(s) tr ts
x,y
Linear 0 1.58 3.72 5.51
Nonlinear 6 1.05 1.52 3.42
z
Linear 0 0.41 1.00 1.55
Nonlinear 0 0.81 2.14 3.28
It should be remarked that the PID controller in the zb is 2 times faster than
the nonlinear controller, which is an important advantage. The effort turns out
to be:
σzlinear
= 2081
σznonlinear
= 1904
Both controllers need almost the same effort. If we define now the effort to
reach a position in the x direction as:
σx = σθ =
t
0
uθ · dt (6.4)
the effort of both controller to reach the [1,0] position are:
σxlinear
= 0.104
σxnonlinear
= 2.053
The nonlinear controller need 20 times more effort to reach the desired po-
sition.
In Figure 6.2c, an external force of 2 N in the x direction has been applied,
being shown the position along this axis. The lineal controller is not able to
absorb the force and come back to the initial position; only after 25 s, when the
quadcopter reaches x = 10.5 m, the error term of the backstepping controller
in high enough to counteract the perturbation and the quadcopter starts slowly
returning to the initial position (not shown in the figure). On the other hand,
the nonlinear controller absorbs the perturbation in within 9 s, keeping the
quadcopter closer than 30 cm from the required position.
The situation when applying a vertical force Dz is similar, but the linear
controller is not able to return to the initial position and only keeps the altitude
at z = −1.6 m (note that the direction of the force is zb). On the contrary, the
nonlinear controller returns slowly to the reference altitude, and also avoids the
quadcopter to increase its altitude more than 0.25 m.
Finally, if an additional mass is added to the quacopter, the nonlinear con-
troller estimates it successfully and returns to the desired altitude in less than
2 s, as can be seen in Figure 6.2e. As it happened when adding an external ver-
tical force, the linear controller can not absorb it and the quadcopter decreases
the altitude because of the additional mass down to 0.42 cm.
49
52. time [s]
0 2 4 6 8 10
X[m]
0
0.2
0.4
0.6
0.8
1
1.2
Reference
Lineal
Non-lineal
(a) Movement in the x direction.
time [s]
0 2 4 6 8 10
Z[m]
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
Reference
Lineal
Non-lineal
(b) Movement in the zb direction.
time [s]
0 2 4 6 8 10
X[m]
0
1
2
3
4
5
6
7
Reference
Lineal
Non-lineal
(c) Movement in the x direction
with non zero Dx.
time [s]
0 2 4 6 8 10
Z[m]
-1.6
-1.5
-1.4
-1.3
-1.2
-1.1
-1
-0.9
Reference
Lineal
Non-lineal
(d) Movement in the zb direction
with non zero Dz.
time [s]
0 2 4 6 8 10
Z[m]
-1.1
-1
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
Reference
Lineal
Non-lineal
(e) Movement in the zb direction
with an additional mass.
Figure 6.2: Comparison of the system position response in the five different
cases considered.
50
53. 6.3 Conclusions
In this master thesis, an analysis of the dynamics of the quadcopter has been
firstly carried out. The first controller, whose design has been based on a lin-
earized model, has been developed for the 3dof and 6dof quadcopter. A good
performance has been achieved, even when tested with a non-linear model. How-
ever, taking a look on the inputs to the electric motors (see Figure (4.5b)), it
looks like that they might be more demanding in order to make the move-
ments faster and in general to make the quadcopter agiler. Moreover, a some
non-realistic behaviors have been assumed, as signals without noise and no aero-
dynamic forces and moments.
Afterwards, another PID controller has been proposed to stabilize the atti-
tude of the six degrees of freedom model, keeping in mind that the parameters
of the model (mass, inertia, etc.) are different. The position control is then con-
structed by using the backstepping method, obtaining a second order system
(Equations 4.5) whose convergence is ensured.
To improve the controller, a similar one is in Chapter 5 presented. This has
a more complex control laws so that external forces and changed in the mass
are considered. The convergence is proved by using Lynapunov functions. The
drawback of this controller is that it is not easy to tune, as it has been seen,
since it has a high number of parameters to be chosen. A genetic algorithm
has been selected to set the parameters, considering some goals for the system
response (system response, overshooting, kick-back behavior, mass and distur-
bance estimation, etc.). The final controller is able to successfully estimate
changes in the mass faster than perturbations, being the desired behavior the
other way around, since external forces, such as wind gusts, might change faster.
Therefore, only constant, or slow changing, perturbations can be successfully
estimated, such as discrepancies with the model.
Finally, both controllers are compared with different tests. In the case of the
attitude stabilization, having a look at the time characteristics of the system
response, it has been shown that the nonlinear controller is faster than the linear
one; on the other hand, the yaw control is faster with the linear one, although
it requires way more effort, approximately 40 times more. Also a perturbation
has been applied in every axes to check the ability to absorb it; the nonlinear
controller recovers the desired input, while the linear controller is not able to
recover it for the attitude angles and for the yaw angles it does, but slower.
For the position control, a comparison of the characteristic time has been also
shown. In the case of horizontal positioning, the nonlinear controller is faster
(the rise time is more than two times shorter) but it needs much more effort.
To control the vertical movement, the linear controller shows faster responses
with approximately the same effort. The rejection of external forces is almost
nonexistent with the linear controller, whereas the nonlinear one absorbs them
successfully. The same situation takes place when there is a change in the
mass of the quadcopter; the nonlinear controller can execute the estimation
of the mass once it takes off and after 5 seconds the mass will be accurately
approximated, and afterwards this term can be disable since no further mass
changes is expected.
As can be seen, the nonlinear controller presents clear advantages over the
linear one. Moreover, we could have checked other robustness indicators, by
assuming another discrepancies between the model and the real system, such
51
54. us changes in the inertial moments, motor responses or propeller misalignment.
If these factors are required to be considered, the genetic algorithm, used to
tune the controller, might take them into account with more tests and weighted
in the fitting function. Any other system response characteristic might also be
considered, modeled and included in the evaluation of each function (such as
maximum rotation speed). This is the main advantage of the here presented
controller, the freedom of adapting the configuration depending on the require-
ments asked to the system. It is important to remark that the more complex
the requirements, or the more number of requirements are needed, the more
difficult the tuning of the GA is, by setting the wights of each characteristic.
52
55. Appendix A
Simulink models
A.1 3dof quadcopter parameters
Parameter Value
m 2.85 kg
d 0.1969 m
dN
1
0.0182 m
Ix 0.0552 kg·m2
Iy 0.0552 kg·m2
Iz 0.1104 kg·m2
ωm 100/15 rad/s
µ 0.5940 N/V
g 9.8 m/s2
Vmax 22 V
Vmin 0 V
pmax
qmax ±40◦
/s
rmax
1Note that the relationship between forces and yaw moment and the voltage to be supplied
to the engines is different from how they are described in the exercise formulation, having now
µ = K and dN = K2/K.
53
56. A.2 6dof quadcopter parameters
Parameter Value
m 1.40 kg
d 0.20 m
dN 0.03 m
Ix 0.03 kg·m2
Iy 0.03 kg·m2
Iz 0.042 kg·m2
ωm 15 rad/s
µ 1 N/V
g 9.8 m/s2
Vmax 20 V
Vmin 0 V
pmax
qmax ±40◦
/s
rmax
54
57. Bibliography
[1] Adamy, J. (2005). Implicit Lyapunov functions and isochrones of linear sys-
tems. IEEE Transactions on Automatic Control, 50(6), 874-879.
[2] Argentim, L. M., Rezende, W. C., Santos, P. E., & Aguiar, R. A. (2013,
May). PID, LQR and LQR-PID on a quadcopter platform. In Informatics,
Electronics & Vision (ICIEV), 2013 International Conference on (pp. 1-6).
IEEE.
[3] Bai, Y., Liu, H., Shi, Z., & Zhong, Y. (2012, July). Robust control of quadro-
tor unmanned air vehicles. In Control Conference (CCC), 2012 31st Chinese
(pp. 4462-4467). IEEE.
[4] Bouabdallah, S., & Siegwart, R. (2005, April). Backstepping and sliding-
mode techniques applied to an indoor micro quadrotor. In Robotics and
Automation, 2005. ICRA 2005. Proceedings of the 2005 IEEE International
Conference on (pp. 2247-2252). IEEE.
[5] Bouffard, P. (2012). On-board Model Predictive Control of a Quadrotor He-
licopter: Design, Implementation, and Experiments (No. UCB/EECS-2012-
241). CALIFORNIA UNIV BERKELEY DEPT OF COMPUTER SCI-
ENCES.
[6] Chen, B. S., Cheng, Y. M., & Lee, C. H. (1995). A genetic approach to
mixed H2/H∞ optimal PID control. Control Systems, IEEE, 15(5), 51-60.
[7] Diao, C., Xian, B., Yin, Q., Zeng, W., Li, H., & Yang, Y. (2011, May). A
nonlinear adaptive control approach for quadrotor UAVs. In Control Con-
ference (ASCC), 2011 8th Asian (pp. 223-228). IEEE.
[8] Dierks, T., & Jagannathan, S. (2010). Output feedback control of a quadro-
tor UAV using neural networks. Neural Networks, IEEE Transactions on,
21(1), 50-66.
[9] Fang, Z., & Gao, W. (2011, July). Adaptive integral backstepping control of
a micro-quadrotor. In Intelligent Control and Information Processing (ICI-
CIP), 2011 2nd International Conference on (Vol. 2, pp. 910-915). IEEE.
[10] Fatan, M., Sefidgari, B. L., & Barenji, A. V. (2013, August). An adap-
tive neuro PID for controlling the altitude of quadcopter robot. In Methods
and Models in Automation and Robotics (MMAR), 2013 18th International
Conference on (pp. 662-665). IEEE.
55
58. [11] Fleming, P. J., & Purshouse, R. C. (2002). Evolutionary algorithms in
control systems engineering: a survey. Control engineering practice, 10(11),
1223-1241.
[12] Giagkiozis, I., & Fleming, P. J. (2015). Methods for multi-objective opti-
mization: An analysis. Information Sciences, 293, 338-350.
[13] Hably, A., Kendoul, F., Marchand, N., & Castillo, P. (2006). Further results
on global stabilization of the PVTOL aircraft. Positive Systems, 303-310.
[14] Hoffmann, G. M., Huang, H., Waslander, S. L., & Tomlin, C. J. (2007, Au-
gust). Quadrotor helicopter flight dynamics and control: Theory and exper-
iment. In Proc. of the AIAA Guidance, Navigation, and Control Conference
(Vol. 2).
[15] Huo, X., Huo, M., & Karimi, H. R. (2014). Attitude stabilization control of
a quadrotor UAV by using backstepping approach. Mathematical Problems
in Engineering, 2014.
[16] Lee, K. U., Kim, H. S., Park, J. B., & Choi, Y. H. (2012, October). Hovering
control of a quadrotor. In Control, Automation and Systems (ICCAS), 2012
12th International Conference on (pp. 162-167). IEEE.
[17] Li, J., & Li, Y. (2011, August). Dynamic analysis and PID control for
a quadrotor. In Mechatronics and Automation (ICMA), 2011 International
Conference on (pp. 573-578). IEEE.
[18] NG TZE HUI, T. H. O. M. A. S. (2007). Design optimization of small-scale
unmanned air vehicles (Doctoral dissertation).
[19] Palunko, I., & Fierro, R. (2011, August). Adaptive control of a quadrotor
with dynamic changes in the center of gravity. In Proceedings 18th IFAC
World Congress (Vol. 18, No. 1, pp. 2626-2631).
[20] Santos, M., Lopez, V., & Morata, F. (2010, November). Intelligent fuzzy
controller of a quadrotor. In Intelligent Systems and Knowledge Engineering
(ISKE), 2010 International Conference on (pp. 141-146). IEEE.
[21] Shen, J. C. (2002). New tuning method for PID controller. ISA transactions,
41(4), 473-484.
[22] Sutarto, H. Y., Budiyono, A., Joelianto, E., & Hiong, G. T. (2006, Decem-
ber). Switched linear control of a model helicopter. In Control, Automation,
Robotics and Vision, 2006. ICARCV’06. 9th International Conference on
(pp.1-8). IEEE.
[23] Yang, Z., & Pedersen, G. (2006, October). Automatic tuning of PID con-
troller for a 1-D levitation system using a genetic algorithm-a real case study.
In Computer Aided Control System Design, 2006 IEEE International Con-
ference on Control Applications, 2006 IEEE International Symposium on
Intelligent Control, 2006 IEEE (pp. 3098-3103). IEEE.
[24] Zulu, A., & John, S. (2014). A Review of Control Algorithms for Au-
tonomous Quadrotors. Open Journal of Applied Sciences, 4(14), 547.
56
